The history of mathematics: A brief course (2013)
Part VI. European Mathematics, 500-1900
Chapter 32. The Calculus Before Newton and Leibniz
The infinite occurs in three forms in calculus: the derivative, the integral, and the power series. Integration, in the form of finding areas and volumes, was developed as a particular theory before the other two subjects came into general use. Although infinite series appear on the horizon, so to speak, in the work of Archimedes on the quadrature of the parabola, as we saw in Chapter 14, they do not come into full view.
As we have also seen, infinitesimal methods were used in geometry by the Chinese and Japanese, and the latter also used infinite series to solve geometric problems (somewhat later than Newton and Leibniz, however). In India, mathematicians had used infinite series a few centuries before the Europeans began to use them, to solve geometric problems via trigonometry. According to Rajagopal (1993), the mathematician Nilakanta, who lived in South India and whose dates are given as 1444–1543, gave a general proof of the formula for the sum of a geometric series. The most advanced of these results is attributed to Madhava (1340–1425), but is definitively stated in the work of Jyesthadeva (1530–ca. 1608):
The product of the given Sine and the radius divided by the Cosine is the first result. From the first,. . .etc., results obtain. . .a sequence of results by taking repeatedly the square of the Sine as the multiplier and the square of the Cosine as the divisor. Divide. . .in order by the odd numbers one, three, etc. . .From the sum of the odd terms, subtract the sum of the even terms. [The result] becomes the arc. [Rajagopal, 1993, p. 98]
These instructions give in words an algorithm that we would write as the following formula, remembering that the Sine and Cosine used in earlier times correspond to our r sin θ and r cos θ, where r is the radius of the circle:
![]()
The bulk of calculus was developed in Europe during the seventeenth century, and it is on that development that the rest of this chapter is focused.
32.1 Analytic Geometry
The creation of what we now know as analytic geometry had to wait for algebraic thinking about geometry (the type of thinking Pappus called analytic) to become a standard mode of thinking. No small contribution to this process was the creation of the modern notational conventions, many of which were due to François Viète and René Descartes. It was Descartes who started the very useful convention of using letters near the beginning of the alphabet for constants and data and those near the end of the alphabet for variables and unknowns. Viète's convention, which was followed by Fermat, had been to use consonants and vowels respectively for these purposes.
32.1.1 Pierre de Fermat
Besides working in number theory, Fermat (1601–1665) studied the works of Apollonius, including references by to lost works. This study inspired him to write a work on plane and solid loci, first published with his collected works in 1679. He used these terms in the sense of Pappus: A plane locus is one that can be constructed using straight lines and circles, and a solid locus is one that requires conic sections for its construction. He says in the introduction that he hopes to systematize what the ancients, known to him from Book 7 of Pappus' Synagomacr1.gifg![]() , had left haphazard. Pappus had written that the locus to more than six lines had hardly been touched. Thus, locus problems were the context in which Fermat invented analytic geometry.
, had left haphazard. Pappus had written that the locus to more than six lines had hardly been touched. Thus, locus problems were the context in which Fermat invented analytic geometry.
Apart from the adherence to a dimensional uniformity that Descartes (finally!) eliminated, Fermat's analytic geometry looks much like what we are now familiar with. He stated its basic principle, asserting that the lines representing two unknown magnitudes should form an angle that would usually be assumed a right angle. He began with the equation of a straight line:1 Z2 − DA = BE. This equation looks strange to us because we automatically (following Descartes) tend to look at the Z as a variable and the A and E as constants, exactly the reverse of what Fermat intended. If we make the replacements Z ![]() c, D
c, D ![]() a, A
a, A ![]() x, B
x, B ![]() b, and E
b, and E ![]() y, this equation becomes c2− ax = by, and now only the exponent on c looks strange, the result of Fermat's adherence to the Euclidean niceties of dimension.
y, this equation becomes c2− ax = by, and now only the exponent on c looks strange, the result of Fermat's adherence to the Euclidean niceties of dimension.
Fermat illustrated the claim of Apollonius that a locus was determined by the condition that the sum of the pairwise products of lines from a variable point to given lines is given. His example was the case of two lines, where—when the two lines are mutually perpendicular—it is the familiar rectangular hyperbola that we have now seen used many times for various purposes. Fermat wrote its equation as ae = z2. He showed that the graph of any quadratic equation in two variables is a conic section.
32.1.2 René Descartes
Fermat's work on analytic geometry was not published in his lifetime, and therefore was less influential than it might have been. As a result, his contemporary René Descartes (1596–1650) is remembered as the creator of analytic geometry, and we speak of “Cartesian” coordinates, even though Fermat was more explicit about their use.
Descartes is remembered not only as one of the most original and creative modern mathematicians, but also as one of the leading voices in modern philosophy and science. Both his scientific work on optics and mechanics and his geometry formed part of his philosophy. Like Plato, he formed a grand project of integrating all of human knowledge into a single system. Also like Plato, he recognized the special place of mathematics in such a system. In his Discourse on Method, published at Leyden in 1637, he explained that logic, while it enabled a person to make correct judgments about inferences drawn through syllogisms, did not provide any actual knowledge about the world, what is usually called empirical knowledge. In what was either a deadpan piece of sarcasm or a sincere tribute to the mystic Ramon Lull (1232–1316), he said that in the art of “Lully” it enabled a person to speak fluently about matters on which he is entirely ignorant. He seems to have agreed with Plato that mathematical concepts are real objects, not mere logical relations among words, and that they are perceived directly by the mind. In his famous attempt at doubting everything, he had brought himself back from total skepticism by deducing the principle that whatever he could clearly and distinctly perceive with his mind must be correct.
As Davis and Hersh (1986) have written, the Discourse on Method was the fruit of a decade and a half of hard work and thinking on Descartes' part, after a series of three vivid dreams on the night of November 10, 1619, when he was a 23-year-old soldier of fortune. The link between Descartes' philosophy and his mathematics lies precisely in the matter of “clear and distinct perception,” for there seems to be no other area of thought in which human ideas are so clear and distinct. As Grabiner (1995, p. 84) says, when Descartes attacked, for example, a locus problem, the answer had to be “it is this curve, it has this equation, and it can be constructed in this way.” Descartes' Géométrie, which contains his ideas on analytic geometry, was published as the last of three appendices to the Discourse.
What Descartes meant by “clear and distinct” ideas in mathematics is shown in a method of generating curves given in his Géométrie that appears mechanical, but can be stated in pure geometric language. A pair of lines intersecting at a fixed point Y coincide initially (Fig. 32.1). The point A remains fixed on the horizontal line. As the oblique line rotates about Y, the point B, which remains fixed on it, describes a circle. The tangent at B intersects the horizontal line at C, and the point on the oblique line directly above C is D. The line perpendicular to the oblique line at D intersects the horizontal line at E, from which a vertical line intersects the oblique line at F, and so forth in a zigzag pattern. Descartes imagined a mechanical linkage that could actually draw these curves.
Figure 32.1 Descartes' linkage for generating curves. The curve x4n = a2(x2 + y2)2n−1 is shown for n = 0, 1, 2, 3.
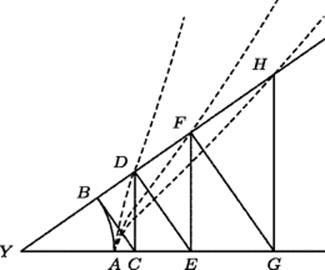
Descartes regarded determinate curves of this sort, depending on one parameter, as we would say, as legitimate to use in geometry. He offered the opinion that the opposition to “mechanical” curves by ancient Greek mathematicians arose because the mechanical curves they knew about—he mentioned the spiral of Archimedes and the quadratix—were indeterminate. In the case of the spiral of Archimedes, which is generated by a point moving at constant linear velocity along a line that is rotating with constant angular velocity, the indeterminacy arises because the two velocities need to be coordinated with infinite precision. For the quadratrix, the same problem arises, since the ratio of the angular velocity of a rotating line and the linear velocity of a translating line needs to be known with infinite precision.
Descartes' Géométrie resembles a modern textbook of analytic geometry less than does Fermat's Introduction to Plane and Solid Loci. He does not routinely use a system of “Cartesian” coordinates, as one might expect from the name. But he does remove the dimensional difficulties that had complicated geometric arguments since Euclid's definition of a ratio.
[U]nity can always be understood, even when there are too many or too few dimensions; thus, if it be required to extract the cube root of a2b2 − b, we must consider the quantity a2b2 divided once by unity, and the quantity bmultiplied twice by unity. [Smith and Latham, 1954, p. 6]
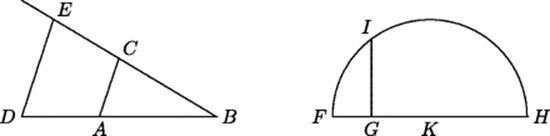
Here Descartes is explaining that all four arithmetic operations can be performed on lines and yield lines as a result. He illustrated the product and square root by the diagrams in Fig. 32.2, where AB = 1 on the left and FG = 1 on the right.
Figure 32.2 Left: AB = 1, so that BE = BC · BD. Right: FG = 1, so that ![]() .
.
Descartes went a step further than Oresme in eliminating dimensional considerations, and he went a step further than Pappus in his classification of locus problems. Having translated these problems into the language of algebra, he realized that the three-and four-line locus problems always led to polynomial equations of degree at most 2 in x and y, and conversely, any equation of degree 2 or less represented a three-or four-line locus. He asserted with confidence that he had solved the problem that Pappus reported unsolved in his day. It was in this context that he formulated the idea of using two intersecting lines as a frame of reference, saying that
since so many lines are confusing, I may simplify matters by considering one of the given lines and one of those to be drawn. . .as the principal lines, to which I shall try to refer all the others. [Smith and Latham, 1954, p. 29]
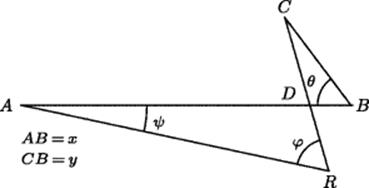
The idea of using two coordinate lines is psychologically very close to the linkages illustrated in Fig. 32.1. In terms of Fig. 32.3, Descartes took one of the fixed lines as a horizontal axis AB, since a line was to be drawn from point C on the locus making a fixed angle θ with AB. He thought of this line as sliding along AB and intersecting it at point B, and he denoted the variable length AB by x. Then since C needed to slide along this moving line so as to keep the proportions demanded by the conditions of the locus problem, he denoted the distance CB by y. All the lines were fixed except CB, which moved parallel to itself, causing x to vary, while on it y adjusted to the conditions of the problem. For each of the other fixed lines, say AR, the angles ψ, θ, and ϕ will all be given, ψ by the position of the fixed lines AB and AR, and the other two by the conditions prescribed in the problem. Since these three angles determine the shape of the triangles ADR and BCD, they determine the ratios of any pair of sides in these triangles through the law of sines, and hence all sides can be expressed in terms of constants and the two lengths x and y. If the set of 2n lines is divided into two sets of n as the 2n-line locus problem requires, the conditions of the problem can be stated as an equation of the form
![]()
where p and q are of degree at most n in each variable. The analysis was mostly “clear and distinct.”
Descartes argued that the locus could be considered known if one could locate as many points on it as desired.2 He next pointed out that in order to locate points on the locus one could assign values to either variable x and y, then compute the value of the other by solving the equation.3
Everyone who has studied analytic geometry in school must have been struck at the beginning by how much clearer and easier it was to use than the synthetic geometry of Euclid. That aspect of the subject is nicely captured in the words the poet Paul Valéry (1871–1945) applied to Descartes' philosophical method in general: “the most brilliant victory ever achieved by a man whose genius was applied to reducing the need for genius” (quoted by Davis and Hersh, 1986, p. 7).
This point was not appreciated by Newton, who, in a rather ungenerous exhibition of his own remarkable mathematical talent (Whiteside, 1967, Vol. IV, pp. 275–283), said that Descartes “makes a great show” about his solution of the three-and four-line locus problems, “as if he had achieved something so earnestly sought after by the ancients.” He also expressed a distaste for Descartes' use of symbolic algebra to solve this problem (a distaste that would be echoed by other mathematicians), saying that if this algebra were written out in words, it “would prove to be so tedious and entangled as to provoke nausea.” One is inclined to say, on Descartes' behalf, “Precisely! That's why it's better to use algebraic symbolism and avoid the tedium, confusion, and nausea.”
Figure 32.3 Descartes' analysis of the n-line locus problem.
32.2 Components of the Calculus
In his comprehensive history of the calculus, Boyer (1949) described “a century of anticipation” during which the application of algebra to geometric problems began to incorporate some of the less systematic parts of ancient geometry, especially the infinitesimal ideas contained in what was called the method of indivisibles. Let us take up the story of calculus at the point where algebra enters the picture, beginning with some elementary problems of finding tangents and areas.
32.2.1 Tangent and Maximum Problems
The main problem in finding a tangent to a curve at a given point is to find some second condition, in addition to passing through the point, that this line must satisfy so as to determine it uniquely. It suffices to know either a second point that it must pass through or the angle that it must make with a given line.
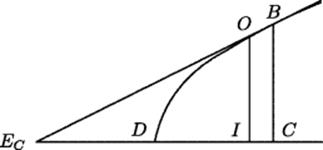
Fermat had attacked the problem of finding maxima and minima of variables even before the publication of Descartes' Géométrie. As his works were not published during his lifetime but only circulated among those who were in a rather select group of correspondents, his work in this area was not recognized for some time. His method is very close to what is still taught in calculus books. The difference is that whereas we now use the derivative to find the slope of the tangent line, that is, the tangent of the angle it makes with a reference axis, Fermat looked for the point where the tangent intercepted that axis. If the two lines did not intersect, as happens at maxima and minima, the tangent was easily determined as the unique parallel through the given point to the given axis. In all other cases Fermat needed to determine the length of the projection of the tangent on the axis from the point of intersection to the point below the point of tangency, a length known as the subtangent. In a letter sent to the monk and mathematician Marin Mersenne (1588–1648) and forwarded to Descartes in 1638, Fermat explained his method of finding the subtangent, which invokes some of the same ideas used earlier by Sharaf al-Tusi (see Chapter 26).
In Fig. 32.4 the curve DB is a parabola with axis CD, and the tangent at B, above the point C, meets the axis at EC. Since the parabola is convex, a point O between B and EC on the tangent lies outside the parabola. That location provided Fermat with two inequalities, one of which was ![]() . (Equality would hold here if
. (Equality would hold here if ![]() were replaced by the portion of it cut off by the parabola.) Since
were replaced by the portion of it cut off by the parabola.) Since ![]() , it follows that
, it follows that ![]() . Then abbreviating by setting
. Then abbreviating by setting ![]() ,
, ![]() , and
, and ![]() , we have g : g − y > x2 : x2 + y2 − 2xy. Cross-multiplying, we obtain
, we have g : g − y > x2 : x2 + y2 − 2xy. Cross-multiplying, we obtain
![]()
Canceling the term gx2 and dividing by y, we obtain gy − 2gx > − x2. Since this inequality must hold for all positive numbers y (no matter how small), it follows that x2 ≥ 2gx, that is, x ≥ 2g if x > 0. That is, ![]() if C is right of the point I, and so
if C is right of the point I, and so ![]() also. Reasoning similarly if C is left of I, shows that
also. Reasoning similarly if C is left of I, shows that ![]() if C is any point left of I, and so
if C is any point left of I, and so ![]() . Having thus ruled out the possibilities
. Having thus ruled out the possibilities ![]() and
and ![]() , Fermat had proved that
, Fermat had proved that ![]() , and thereby solved the problem. In this argument, Fermat was relying on the Archimedean trichotomy. His argument can be formulated as a limiting argument, but it is perfectly rigorous in the finite terms in which he stated it.
, and thereby solved the problem. In this argument, Fermat was relying on the Archimedean trichotomy. His argument can be formulated as a limiting argument, but it is perfectly rigorous in the finite terms in which he stated it.
Figure 32.4 Fermat's method of finding the subtangent.
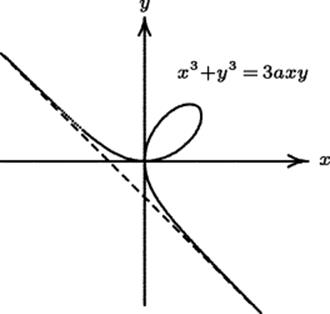
In this paper Fermat asserted, “And this method never fails. . ..” This assertion provoked an objection from Descartes,4 who used circles in a very similar way to find the normal to a curve at a point. (We do not have space to discuss that method.) Descartes challenged Fermat with the curve of Fig. 32.5, now known as the folium of Descartes, having equation x3 + y3 = 3axy.
Figure 32.5 The folium of Descartes. Descartes and Fermat considered only the loop in this curve.
As already mentioned, Descartes did not regard curves such as the spiral and the quadratrix as admissible in argument, since they are generated by two motions whose relationship to each other cannot be determined exactly. A few such curves, however, were to prove a very fruitful source of new constructions and applications. One of them, which had first been noticed in the early sixteenth century by an obscure mathematician named Charles Bouvelles (ca. 1470–ca. 1553), is the cycloid, the curve generated by a point on a circle (called the generating circle) that rolls without slipping along a straight line. It is easily pictured by imagining a painted spot on the rim of a wheel as the wheel rolls along the ground. Since the speed of the rim about its center is exactly equal to the linear speed of the center, it follows that the point is at any instant moving along the bisector of the angle formed by a horizontal line and the tangent to the generating circle. In this way, given the generating circle, it is an easy matter to construct the tangent to the cycloid. This result was obtained independently around 1638 by Descartes, Fermat, and Gilles Personne de Roberval (1602–1675), and slightly later by Evangelista Torricelli (1608–1647), a pupil of Galileo Galilei (1564–1642).
32.2.2 Lengths, Areas, and Volumes
Seventeenth-century mathematicians had inherited two conceptually different ways of applying infinitesimal ideas to find areas and volumes. One was to regard an area as a “sum of lines.” The other was to approximate the area by a sum of regular figures and try to show that the approximation got better as the individual regular figures got smaller. The rigorous version of the latter argument, the method of exhaustion, based on the Archimedean trichotomy was tedious and of limited application.
32.2.3 Bonaventura Cavalieri
In the “sum of lines” approach, a figure whose area or volume was required was sliced into parallel sections, and these sections were shown to be equal or proportional to corresponding sections of a second figure whose area or volume was known. The first figure was then asserted to be equal or proportional to the second. The principle was stated in 1635 by Bonaventura Cavalieri (1598–1647), a Jesuit priest and a student of Galileo. At the time it was customary for professors to prove their worthiness for a chair of mathematics by a learned dissertation. Cavalieri proved certain figures equal by pairing off congruent sections of them, in a manner similar to Archimedes' Method and the method by which Zu Chongzhi and Zu Geng found the volume of a sphere. This method implied that figures in a plane lying between two parallel lines and such that all sections parallel to those lines have the same length must have equal area. This principle is now called Cavalieri's principle. The idea of regarding a two-dimensional figure as a sum of lines or a three-dimensional figure as a sum of plane figures was extended by Cavalieri to consideration of the squares on the lines in a plane figure, then to the cubes on the lines in a figure, and so on.
To see how his reasoning works, we give a sample. Figure 32.6 shows an isosceles right triangle ABC of side AB = a = BC, completed to form the square ABCF. The “sum of the lines” such as DE inside this triangle is simply its area, namely a2/2. The sum of the lines in the triangle AHK, whose sides are only half as large, is one-fourth of this area, or a2/8. (One can see this by letting each line BE correspond to the line only half as far from A as B is. That line will be only half as long as BE, and the total length along which the new lines are “summed” will also be only half as long.) Cavalieri undertook to find a similar expression for the sum of the squares of the lines, which we would interpret as the area under the curve y = x2. The sum of the portion of these squares that lie between A and H is one-eighth of the full sum, since again one can imagine summing the squares of the lines only half as far away from A, which are only one-fourth as long, and the length along which they are summed is only half of side AB.
Figure 32.6 The sum of the powers of the lines in a triangle, according to Cavalieri.
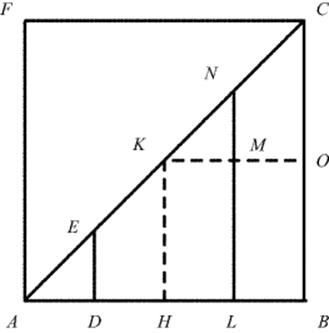
The sum of all the squares inside ABC is the sum of all the squares DE2 inside triangle AHK, plus the sum of all the squares LN2 inside the trapezoid HBCK. But since LN = LM + MN = a/2 + MN, we see that the latter sum is the sum of all the squares MN2 inside KOC (which is the same as the sum of all the squares DE2 inside AHK) plus a times the sum of all the lines MN inside KOC (which is a3/8), plus another a3/8 for the sum of the squares a2/4 of the lines inside the square HBOK. Altogether then, the sum of the squares of the lines inside ABC is twice the sum of the squares of the lines inside AHK, plus a3/4. Since the sum of the squares of the lines inside AHK is one-eighth of the sum of the squares of the lines inside ABC, it follows that three fourths of the latter sum is a3/4, and therefore the sum is a3/3. In this way, Cavalieri established what is equivalent to the formula ![]() . More generally, using the binomial expansion of (a/2 + MN)n just as we did here in the case n = 2, he established the equivalent of
. More generally, using the binomial expansion of (a/2 + MN)n just as we did here in the case n = 2, he established the equivalent of ![]() .
.
32.2.4 Gilles Personne de Roberval
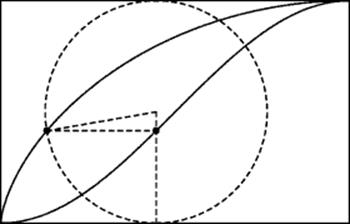
Cavalieri's principle was applied to find the area of the cycloid. Roberval (1602–1675), who found the tangent to the cycloid, also found the area beneath it by a clever use of Cavalieri's principle. He considered along with half an arch of the cycloid itself a curve he called the companion to the cycloid. This companion curve is generated by a point that is always directly below or above the center of the generating circle as it rolls along and at the same height as the point on the rim that is generating the cycloid. As the circle makes half a revolution (see Fig. 32.7), the cycloid and its companion first diverge from the ground level, then meet again at the top. Symmetry considerations show that the area under the companion curve is exactly one-half of the rectangle whose vertical sides are the initial and final positions of the diameter of the generating circle through the point generating the cycloid. But by definition of the two curves their generating points are always at the same height, and the horizontal distance between them at any instant is half of the corresponding horizontal section of the generating circle. Hence by Cavalieri's principle the area between the two curves is exactly half the area of the circle.
Figure 32.7 Roberval's quadrature of the cycloid.
32.2.5 Rectangular Approximations and the Method of Exhaustion
Besides the method of indivisibles (Cavalieri's principle), mathematicians of the time also applied the method of polygonal approximation, that is, the method of exhaustion to find areas. This method, as we saw in Chapter 14, was used by Archimedes to find the area of a parabolic segment and was completely rigorous from the Euclidean point of view. In 1640, Fermat wrote a paper on quadratures in which he found the areas under certain figures by this method. He was somewhat sketchier in the details than Archimedes had been, but that was because he referred explicitly to Archimedes' work, saying that “it suffices to make this remark once and for all, and there is no need to refer constantly to a technique that is well known to mathematicians.” In other words, as we see from examining what Fermat wrote, all the basic ideas of the analysis were already present in the work of Archimedes, and what had been lacking was an algebraic language to make the expression of those ideas more transparent. That language is what Fermat supplied.
He considered a “generalized hyperbola,” as in Fig. 32.8, a curve referred to asymptotes AR and AC and defined by the property that the ratio AHm : AGm = EGn : HIn is the same for any two points E and I on the curve; we would describe this property by saying that xmyn = const.
Figure 32.8 Fermat's quadrature of a generalized hyperbola.
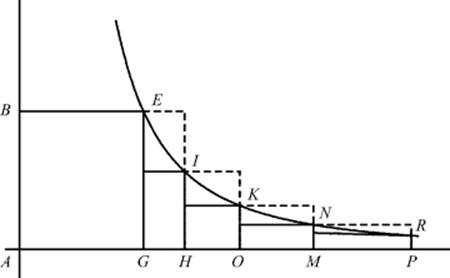
The case n = 1, m = 2 is illustrated in Fig. 32.6, where the abscissas AG, AH, AO, AM, AR, . . . increase geometrically, that is AG/AH = AH/AO = AO/AM = AM/AR,. . ., and the ordinates EG, IH, NO, PM, SR, . . . are inversely proportional to the squares of the corresponding abscissas. As we would write this relation, EG = k/AG2, and so on. From these relations, it is not difficult to see that the area S under the curve from G to infinity satisfies
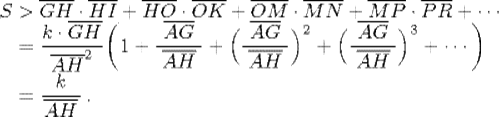
And similarly,
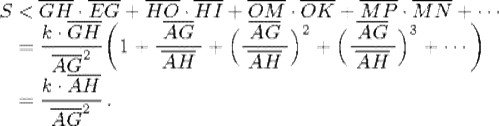
When H is taken sufficiently close to G, both of these expressions can be made as close to ![]() , that is, to
, that is, to ![]() , as desired. Hence, the rectangle AGEB must be the required area. We would now phrase this result as
, as desired. Hence, the rectangle AGEB must be the required area. We would now phrase this result as
![]()
32.2.6 Blaise Pascal
As shown above, Cavalieri found the “sums of the powers of the lines” inside a triangle, which makes it possible to find the area under a curve y = xn between any two values x = a and x = b. Naturally, one would like to be able to do the same for the portion of a semicircle ![]() cut off between two chords x = a and x = b. Thus instead of summing the lines xn from x = a to x = b, we would like to sum the lines
cut off between two chords x = a and x = b. Thus instead of summing the lines xn from x = a to x = b, we would like to sum the lines ![]() . The technique we illustrated above will not help, since the portion of the sum in the first half of the interval has no simple relation to the whole sum, and the binomial expansion of
. The technique we illustrated above will not help, since the portion of the sum in the first half of the interval has no simple relation to the whole sum, and the binomial expansion of ![]() in terms of MN is infinite and very messy. How is this problem to be solved? To explain it, we shall introduce a bit of later notation due to Leibniz to clarify what Cavalieri was actually doing. He wasn't actually summing all the x2 between x = 0 and x = a. Rather, he was summing x2 dx, where dx is an “infinitely short” portion of the x-axis. The technical basis for his results, as shown in the example given above, was the use of the binomial theorem to break the sum of powers of lines inside a rectangle into the portions above and below the diagonal. That technique will not work for a circle, where instead of powers of x, one needs to consider lines of length
in terms of MN is infinite and very messy. How is this problem to be solved? To explain it, we shall introduce a bit of later notation due to Leibniz to clarify what Cavalieri was actually doing. He wasn't actually summing all the x2 between x = 0 and x = a. Rather, he was summing x2 dx, where dx is an “infinitely short” portion of the x-axis. The technical basis for his results, as shown in the example given above, was the use of the binomial theorem to break the sum of powers of lines inside a rectangle into the portions above and below the diagonal. That technique will not work for a circle, where instead of powers of x, one needs to consider lines of length ![]() . To find the quadrature of the circle, it is necessary to change to a new variable, namely the polar angle ϕ, and express dx in terms of dϕ. That feat was achieved by Blaise Pascal (1623–1662) in 1659.
. To find the quadrature of the circle, it is necessary to change to a new variable, namely the polar angle ϕ, and express dx in terms of dϕ. That feat was achieved by Blaise Pascal (1623–1662) in 1659.
Pascal found the “sums of the powers of the lines inside a quadrant of a circle.” Now a line inside a quadrant of a circle is what up to now has been called a sine. Thus, Pascal found the sum of the powers of the sines of a quadrant of a circle. Ordinarily, as we have repeatedly seen, the geometric interpretation of this sum would be as the area under the curve. However, that will not work in this case. To keep the reasoning clear (or, rather, as clear as it could be at the time, since he was using actual infinitesimal arguments, in contrast to Fermat), Pascal distinguished between a sine and an ordinate. We can keep this distinction clear by noting that it is all a matter of which variable is regarded as the independent variable. The ordinate is ![]() and refers to rectangular coordinates (x, y). The sine is R sin ϕ and refers to what we call polar coordinates (ϕ, r). Thus, the “sum of the sines” is carried out only over an infinitesimal arc, which must be imagined as having been straightened out (rectified) and turned into a portion of the tangent.5 The area under the curve is the sum of the ordinates, which we can't find. Pascal managed to express the sum of the ordinates in terms of the sum of the sines, which he was able to find.
and refers to rectangular coordinates (x, y). The sine is R sin ϕ and refers to what we call polar coordinates (ϕ, r). Thus, the “sum of the sines” is carried out only over an infinitesimal arc, which must be imagined as having been straightened out (rectified) and turned into a portion of the tangent.5 The area under the curve is the sum of the ordinates, which we can't find. Pascal managed to express the sum of the ordinates in terms of the sum of the sines, which he was able to find.
Pascal argued that when a finite arc is divided into infinitely many equal small pieces, those pieces are equal to the portions of the tangent cut off between the two bounding ordinates. He acknowledged that the arc and the tangent were not equal with only a finite number of divisions, but claimed that they were equal with an infinite number. Thus he took the plunge into an actual infinity. This was a bold step beyond what the Greeks and Fermat would have admitted. This argument was logically shaky at the time, but the intuitive riches that Leibniz reaped from it ultimately justified a few centuries of doubt and uncertainty as to its validity. To see what Pascal did, refer to Fig. 32.9.
Figure 32.9 Pascal's infinitesimal triangle method of finding the sum of the sines in a quadrant.
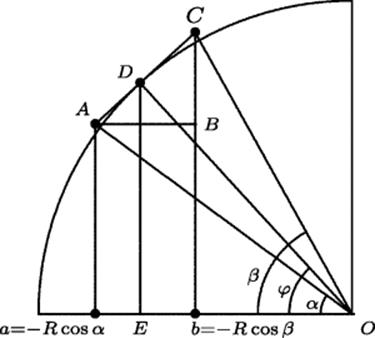
We would like to sum the infinitely thin rectangles ![]() , but the algebraic techniques used by Cavalieri and Fermat do not allow us to do so. By approximating a small piece of arc of length d(Rϕ) = R(β − α) by the tangent AC, and drawing the radius AD to the point of tangency, we get an infinitesimal triangle ABC that is similar to the finite triangle DEO, whence it follows that OD · AB = AC · DE. Now, AB = R(cos α − cos β) = d(R cos ϕ), OD = R, AC = d(Rϕ), and DE = R sin ϕ. Thus we have the infinitesimal relation
, but the algebraic techniques used by Cavalieri and Fermat do not allow us to do so. By approximating a small piece of arc of length d(Rϕ) = R(β − α) by the tangent AC, and drawing the radius AD to the point of tangency, we get an infinitesimal triangle ABC that is similar to the finite triangle DEO, whence it follows that OD · AB = AC · DE. Now, AB = R(cos α − cos β) = d(R cos ϕ), OD = R, AC = d(Rϕ), and DE = R sin ϕ. Thus we have the infinitesimal relation
![]()
and it is clear that R can be divided out of this relation. Pascal expressed this result by saying that the sum of the sines of any arc is equal to the portion of the base between the extreme sines [that is,R cos α − R cos β] multiplied by the radius.
In terms of the rectangular coordinates x and y, the differential relation says dx = R sin ϕ dϕ. Hence to find the area (the sum of the ordinates, in Pascal's language) from ϕ = 0 to ϕ = β, we would have to sum R sin ϕ dx = R2 sin 2ϕdϕ. Pascal did so, and determined correctly that the sum of the squares of those sines is equal to the sum of the ordinates that lie between the extreme sines.
However, we are getting ahead of the story by talking about differential relations. As noted, the concept of a differential was due to Leibniz, inspired by precisely the work of Pascal that we are discussing here.
In modern terms, where Cavalieri found ![]() , Pascal found
, Pascal found ![]() .
.
32.2.7 The Relation Between Tangents and Areas
The first statement of a relation between tangents and areas appears in 1670 in a book entitled Lectiones geometricae by Isaac Barrow (1630–1677), a professor of mathematics at Cambridge and later chaplain to Charles II. Barrow gave the credit for this theorem to “that most learned man, Gregory of Aberdeen” (James Gregory, 1638–1675). Barrow states several theorems resembling the fundamental theorem of calculus. The first theorem (Section 11 of Lecture 10) is the easiest to understand. Given a curve referred to an axis, Barrow constructs a second curve such that the ordinate at each point is proportional to the area under the original curve up to that point. We would express this relation as ![]() , where y = f(x) is the first curve, y = F(x) is the second, and 1/R is the constant of proportionality. If the point T = (t, 0) is chosen on the axis so that (x − t) · f(x) = RF(x), then, said Barrow, Tis the foot of the subtangent to the curve y = F(x); that is, x − t is the length of the subtangent. In modern language the length of the subtangent to the curve y = F(x) is |F(x)/F' (x)|. This expression would replace (x − t) in the equation given by Barrow. If both F(x) and F' (x) are positive, this relation really does say that
, where y = f(x) is the first curve, y = F(x) is the second, and 1/R is the constant of proportionality. If the point T = (t, 0) is chosen on the axis so that (x − t) · f(x) = RF(x), then, said Barrow, Tis the foot of the subtangent to the curve y = F(x); that is, x − t is the length of the subtangent. In modern language the length of the subtangent to the curve y = F(x) is |F(x)/F' (x)|. This expression would replace (x − t) in the equation given by Barrow. If both F(x) and F' (x) are positive, this relation really does say that ![]() .
.
Later, in Section 19 of Lecture 11, Barrow shows the other version of the fundamental theorem, that is, that if a curve is chosen so that the ratio of its ordinate to its subtangent (this ratio is precisely what we now call the derivative) is proportional to the ordinate of a second curve, the area under the second curve is proportional to the ordinate of the first.
32.2.8 Infinite Series and Products
The methods of integration requiring the summing of infinitesimal rectangles or all the lines inside a plane figure led naturally to the consideration of infinite series. Several special series were known by the mid-seventeenth century. For example, the Scottish mathematician James Gregory published a work on geometry in 1668 in which he stated the equivalent of the formula given earlier (unbeknown to Gregory, of course) by Jyesthadeva:
![]()
Infinite product expansions were known by this time for the number π. One, due to John Wallis (1616–1703), is
![]()
32.2.9 The Binomial Series
It was the binomial series that really established the use of infinite series in analysis. The expansion of a power of a binomial leads to finite series when the exponent is a nonnegative integer and to an infinite series otherwise. This series, which we now write in the form
![]()
was discovered by Newton around 1665, although he expressed it in a different language, as a recursive procedure for finding the terms. In a 1676 letter to Henry Oldenburg (1615–1677), Secretary of the Royal Society, Newton wrote this expansion as
![]()
“where P + PQ stands for a quantity whose root or power or whose root of a power is to be found, P being the first term of that quantity, Q being the remaining terms divided by the first term and m/n the numerical index of the powers of P + PQ. . . A stands for the first term ![]() , B for the second term
, B for the second term ![]() , and so on. . . .”
, and so on. . . .”
Newton's explanation of the meaning of the terms A, B, C,. . ., means that the kth term is obtained from its predecessor via multiplication by {[(m/n) − k]/(k + 1)}Q. He said that m/n could be any fraction, positive or negative.
The entrance of Newton into this arena was to lead to revolutionary changes in the way people thought about the myriad techniques and principles that made up the subject that was soon to become the calculus. That story forms the subject of our next chapter.
Problems and Questions
Mathematical Problems
32.1 Show that the Madhava–Jyesthadeva formula given at the beginning of the chapter is equivalent to
![]()
or, letting x = tan θ,
![]()
32.2 Referring to Fig. 32.6, show that the rectangle containing half of the cycloidal arch has length equal to the circumference of the circle and height equal to its diameter, and so, because of Archimedes' result that a circle equals a right triangle having one leg equal to its circumference and the other equal to its radius, that rectangle is exactly twice as large as the circle generating the cycloid. Use that and Roberval's result to show that the area under one full arch of a cycloid is exactly three times the area of the generating circle.
32.3 Consider an ellipse with semiaxes a and b (a > b) and a circle of radius b, the center of the circle lying on the extension of the major axis of the ellipse. Show that for every line parallel to major axis of the ellipse, the portion of that line inside the ellipse will be a/b times the portion inside the circle. Use this fact and Cavalieri's principle to compute the area of the ellipse. This result was given by Kepler.
Historical Questions
32.4 What differences are noticeable between analytic geometry as developed by Fermat and by Descartes?
32.5 What major innovation in the application of geometry to algebra is due to Descartes?
32.6 Which infinite series were the first to be introduced, and what was the motive for introducing them?
Questions for Reflection
32.7 What methodological techniques inherited from Euclidean geometry had to be ignored in order to apply algebra to geometry?
32.8 The philosopher Bertrand Russell wrote (1945, p. 36), “When Descartes introduced coordinate geometry, thereby again making arithmetic supreme [above geometry], he assumed the possibility of a solution to the problem of incommensurables, though in his day no such solution had been found.” What is the “problem of incommensurables” that Russell is referring to, and on what grounds can one conclude that Descartes was ignoring the difficulty?
32.9 Given the large number of tangent and area problems solved by the mid-seventeenth century, what was still needed before one could say that calculus had arisen?
Notes
1. Fermat actually wrote “Zpl. − D in A æquetur B in E.” That is, “Let Z2 − DA equal BE.”
2. The validity of this claim is somewhat less than “clear and distinct.”
3. This claim also involves a great deal of hope, since equations of degree higher than 4 were unknown territory in his day.
4. There was little love lost between Descartes and Fermat, since Fermat had dismissed Descartes' derivation of the law of refraction. [Descartes assumed that light traveled faster in denser media; Fermat assumed that it traveled slower. Yet they both arrived at the same law! For details, see Indorato and Nastasi 1989).] Descartes longed for revenge, and even though he eventually ended the controversy over Fermat's methods with a grudging half-acknowledgment that Fermat was right, he continued to attack Fermat's construction of the tangent to a cycloid.
5. Leibniz, who was inspired by Pascal's infinitesimal triangle, showed that the chord would work just as well as the tangent.