The history of mathematics: A brief course (2013)

Part VI. European Mathematics, 500-1900

Chapter 33. Newton and Leibniz

The discoveries described in the preceding chapter show that the essential components of calculus were recognized by the mid-seventeenth century, like the pieces of a jigsaw puzzle lying loose on a table. What was needed was someone to see the pattern and fit all the pieces together. The unifying principle was the concept of a derivative, and that concept came to Newton and Leibniz independently and in slightly differing forms.

33.1 Isaac Newton

Isaac Newton was born prematurely on Christmas day in 1642. (When the British adopted the Gregorian calendar in 1752, eleven days had to be removed as an adjustment from the earlier Julian calendar. As a result, on what is called the proleptic Gregorian calendar, his actual birthday was January 4, 1643.) His parents were minor gentry, but his father had died before his birth. The midwife who attended his mother is said to have predicted that the child would not live out the day. Medical predictions are notoriously unreliable, and this one was wrong by 85 years! He was 6 years old when the English Civil War began, and the rest of his childhood was spent in that turbulent period. He attended a neighborhood school, and though not a particularly good student, he exhibited enough talent to motivate his uncle to send him to Cambridge University, which he entered about the time of the restoration of Charles II to the throne. Although he was primarily interested in chemistry, he did buy and read not only Euclid's Elements but also some of the current treatises on algebra and analytic geometry. From 1663 on he attended the lectures of Isaac Barrow.

Due to an outbreak of plague in 1665, he returned to his family home at Woolsthorpe, and during the next two years, while the University was closed, he alternated between Woolsthorpe and his rooms in Cambridge, pursuing his own mathematical and physical researches. He was a careful observer and experimenter, and this period was, as he later recalled, the most productive of his life. Besides the binomial theorem already discussed, he discovered the general use of infinite series and what he called the method of fluxions. His early notes on the subject were not published until after his death, but a revised version of the method was expounded in his Principia.

33.1.1 Newton's First Version of the Calculus

Newton first developed the calculus in what we would call parametric form. Time was the universal independent variable, and the relative rates of change of other variables were computed as the ratios of their rates of change with respect to time. Newton thought of variables as moving quantities and focused attention on their velocities. He used the letter o to represent a small time interval and p for the velocity of the variable x, so that the change in x over the time interval o was op. Similarly, using q for the velocity of y, if y and x are related by yⁿ = x^m, then (y + oq)ⁿ = (x + op)^m. Both sides can be expanded by the binomial theorem. Then if the equal terms yⁿ and x^m are subtracted, all the remaining terms are divisible by o. When o is divided out, one side is nqyⁿ⁻¹ + oA and the other is mpx^m−1 + oB. Ignoring the terms containing o, since o is small, one finds that the relative rate of change of the two variables, q/p is given by q/p = (mx^m−1)/(nyⁿ⁻¹); and since y = x^m/n, it follows that q/p = (m/n)x^(m/n)−1. Here at last was the concept of a derivative, expressed as a relative rate of change.

Newton recognized that reversing the process of finding the relative rate of change provides a solution of the area problem. He was able to find the area under the curve y = ax^m/n by working backward.

33.1.2 Fluxions and Fluents

Newton's “second draft” of the calculus was the concept of fluents and fluxions. A fluent is a moving or flowing quantity; its fluxion is its rate of flow, which we now call its velocity or derivative. In his Fluxions, written in Latin in 1671 and published in 1742 (an English translation appeared in 1736), he replaced the notation p for velocity by , a notation still used in mechanics and in the calculus of variations. Newton's notation for the opposite operation, finding a fluent from the fluxion, is no longer used. Instead of ∫x(t) dt, he wrote .

The first problem in the Fluxions is: The relation of the flowing quantities to one another being given, to determine the relation of their fluxions. The rule given for solving this problem is to arrange the equation that expresses the given relation (assumed algebraic) in increasing integer powers of one of the variables, say x, multiply its terms by any arithmetic progression (that is, the first power is multiplied by c, the square by 2c, the cube by 3c, etc.), and then multiply by . After this operation has been performed for each of the variables, the sum of all the resulting terms is set equal to zero.

Newton illustrated this operation with the relation x³ − ax² + axy − y² = 0, for which the corresponding fluxion relation is , and by numerous examples of finding tangents to well-known curves such as the spiral and the cycloid. Newton also found their curvatures and areas. The combination of these techniques with infinite series was important, since fluents often could not be found in finite terms. For example, Newton found that the area under the curve was given by the Jyesthadeva–Gregory series .

33.1.3 Later Exposition of the Calculus

Newton made an attempt to explain fluxions in terms that would be more acceptable logically, calling it the “method of initial and final ratios,” in his treatise on mechanics, the Philosophiae naturalis principia mathematica(Mathematical Principles of Natural Philosophy), where he said the following:

Quantities, and the ratios of quantities, which in any finite time converge continually toward equality, and before the end of that time approach nearer to each other than by any given difference, become ultimately equal.

If you deny it, suppose them to be ultimately unequal, and let D be their ultimate difference. Therefore they cannot approach nearer to equality than by that given difference D; which is contrary to the supposition.

If only the phrase become ultimately equal had some clear meaning, as Newton seemed to assume, this argument might have been convincing. As it is, it comes close to being a definition of ultimately equal, or, as we would say, equal in the limit. Newton came close to stating the modern concept of a limit at another point in his treatise, when he described the “final ratios” (derivatives) as “limits towards which the ratios of quantities decreasing without limits do always converge, and to which they approach nearer than by any given difference.” Here one can almost see the “arbitrarily small ε” that plays the central role in the modern definition of a limit.

33.1.4 Objections

Newton anticipated some objections to these principles, and in his Principia, tried to phrase his exposition of the method of initial and final ratios in such a way as not to outrage anyone's logical scruples. He said:

It may be objected that there is no final ratio of vanishing quantities, because before they vanish their ratio is not the final one, and after they vanish, they have no ratio. But that same argument would imply that a body arriving at a certain place and stopping there has no final velocity, because the velocity before it arrived was not its final velocity; and after it arrived, it had no velocity. But the answer is easy: the final velocity is the velocity the body has at the exact instant when it arrives, not before or after.

Was this explanation adequate? Do human beings in fact have any conception of what is meant by an instant of time? Do we have a clear idea of the velocity of a body at the very instant when it stops moving? Or do some people only imagine that we do? We are here very close to the arrow paradox of Zeno. At any given instant, the arrow does not move; therefore it is at rest. How can there be a motion (a traversal of a positive distance) as a result of an accumulation of states of rest, in each of which no distance is traveled? Newton's “by the same argument” practically invited the further objection that his attempted explanation merely stated the same fallacy in a new way.

33.2 Gottfried Wilhelm von Leibniz

The codiscoverer with Newton of the calculus was, like Newton, a man involved in public life, but a much more amiable character. The philosopher Bertrand Russell, who had studied Leibniz and understood him better than anyone else, proclaimed him not an admirable man. According to Russell, Leibniz developed a profound philosophy, which he kept secret, knowing that it would not be popular, and published instead only a fatuous optimism aimed at winning friends. Leibniz, the optimistic philosopher, was parodied in the character of Dr. Paingloss in Voltaire's Candide.

As was the case with Newton, Leibniz had wide-ranging interests as a youth and focused on mathematics only in early adulthood. He was born in Leipzig in 1646, more than three years later than Newton, and entered the university there in 1661, at the age of 15. Like Descartes, Fermat and Viète, he studied the law, but was considered too young to be awarded the degree of doctor of laws when he finished his course at the age of 20. He entered the service of the Elector of Mainz as a diplomat and finally came to serve the Electors of Hannover for four decades, including the future King George I of Britain, who succeeded Queen Anne in 1714. In contrast to the prickly, anti-social Newton, he was an urbane, tolerant man, who worked diplomatically in an attempt to reunite the Catholic and Protestant churches, and it was his suggestion to Tsar Peter I (1682–1726) that the Russian Academy of Sciences be founded. This was done the year before Peter died, and many talented mathematicians, including Daniel Bernoulli and Leonhard Euler, did some of their best work there.

During his lifetime, France was militarily powerful while Germany was divided and weak. As servant of several German princes, Leibniz attempted to shield Germany from the power of the French by diverting the interests of Louis XIV toward a holy war against the Ottoman Empire in Egypt. It was during a mission to Paris in 1672 that Leibniz became interested in mathematics and began to read the writings of Pascal. The following year he visited London and met some members of the Royal Society, including the secretary Henry Oldenburg and the librarian James Collins (1625–1683). He kept a diary of this journey on a sheet of paper ruled into columns headed Chemistry, Mechanica, Magnetica, Botanica, and so on. Under mathematics the notes are very sparse, containing only a reference to a general method of finding tangents, probably derived from the lectures of Barrow, which he had bought.

From this time on, Leibniz studied mathematics in earnest and within a decade had derived most of the calculus in essentially the form we know it today. His approach to the subject, in particular the delicate notion of the meaning to be assigned to the limiting ratio of two quantities as they vanish, is quite different from Newton's.

33.2.1 Leibniz’ Presentation of the Calculus

Leibniz believed in the reality of infinitesimals, quantities so small that any finite sum of them is still less than any assignable positive number, but which are nevertheless not zero, so that one is allowed to divide by them. The three kinds of numbers (finite, infinite, and infinitesimal) could, in Leibniz’ view, be multiplied by one another, and the result of multiplying an infinite number by an infinitesimal might be any one of the three kinds. This position was rejected in the nineteenth century but was resurrected in the twentieth century and made logically sound. It lies at the heart of what is called nonstandard analysis, a subject that has not penetrated the undergraduate curriculum. The radical step that must be taken in order to believe in infinitesimals is a rejection of the Archimedean principle that for any two positive quantities of the same kind, some finite number of bisections of the first will produce a quantity smaller than the second. This principle was essential to the use of the method of exhaustion, which was one of the crowning glories of Euclidean geometry. It is no wonder that mathematicians were reluctant to give it up.

Leibniz invented the expression dx to indicate the difference of two infinitely close values of x, dy to indicate the difference of two infinitely close values of y, and dy/dx to indicate the ratio of these two values. This notation was beautifully intuitive and is still the preferred notation for thinking about calculus. Its logical basis at the time was questionable, since it avoided the objections listed above by claiming that the two quantities have not vanished at all but have yet become less than any assigned positive number. However, at the time, consistency would have been counterproductive in mathematics and science.

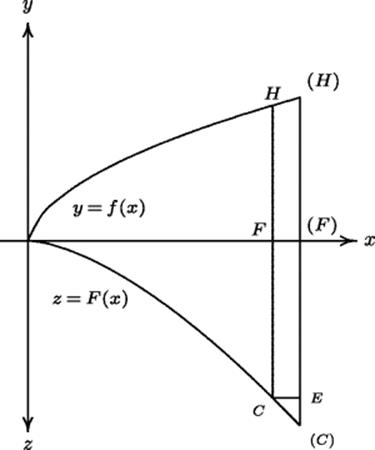
The integral calculus and the fundamental theorem of calculus flowed very naturally from Leibniz’ approach. Leibniz could argue that the ordinates to the points on a curve represent infinitesimal rectangles of height y and width dx, and hence finding the area under the curve—“summing all the lines in the figure”—amounted to summing infinitesimal increments of area dA, which accumulated to give the total area. Since it was obvious that, on the infinitesimal level, dA = y dx, the fundamental theorem of calculus was an immediate consequence. Leibniz first set it out in geometric form in a paper on quadratures in the 1693 Acta eruditorum, a scholarly journal founded by the philosopher Otto Mencke (1644–1707) in Leipzig in 1682. In that paper, Leibniz considered two curves: one, which we would now write as y = f(x), with its graph above a horizontal axis, the other, which we write as z = F(x), with its graph below the horizontal axis.¹ The second curve has an ordinate proportional to the area under the first curve. That is, for a positive constant a, having the dimension of length, aF(x) is the area under the curve y = f(x) from the origin up to the point with abscissa x. We would write the relation now as²

In this form the relation is dimensionally consistent. What Leibniz proved was that the curve z = F(x), which he called the quadratrix (squarer), could be constructed from its infinitesimal elements. In Fig. 33.1, the parentheses around letters denote points at an infinitesimal distance from the points denoted by the same letters without parentheses. In the infinitesimal triangle CE(C) the line E(C) represents dF, while the infinitesimal quadrilateral HF(F)(H) represents dA, the element of area under the curve. The lines F(F) and CE both represent dx. Leibniz argued that by construction, a dF = f(x) dx, and so dF : dx = f(x) : a. That meant that the quadratrix could be constructed by antidifferentiating f(x).

Figure 33.1 Leibniz’ proof of the fundamental theorem of calculus.

Leibniz eventually abbreviated the sum of all the increments in the area (that is, the total area) using an elongated S, so that A = ∫ dA = ∫ y dx. Nearly all the basic rules of calculus for finding the derivatives of the elementary functions and the derivatives of products, quotients, and so on, were contained in Leibniz’ 1684 paper on his method of finding tangents. He had obtained these results several years earlier. His collected works contain a paper written in Latin with the title Compendium quadraturæ arithmeticæ, to which the editor assigns a date of 1678 or 1679. This paper shows Leibniz’ approach through infinitesimal differences and their sums and suggests that it was primarily the problem of squaring the circle and other conic sections that inspired this work, which consists of 49 propositions and two problems. Most of the propositions are stated without proof. Among them are the Taylor series expansions of logarithms, exponentials, and trigonometric functions.

33.2.2 Later Reflections on the Calculus

Like Newton, Leibniz felt the need to answer objections to the new methods of the calculus. In the Acta eruditorum of 1695 Leibniz published a “Response to certain objections raised by Herr Bernardo Niewentiit³ regarding differential or infinitesimal methods.” These objections were three: (1) that certain infinitely small quantities were discarded as if they were zero⁴; (2) the method could not be applied when the exponent is a variable; and (3) the higher-order differentials were inconsistent with Leibniz’ claim that only geometry could provide the necessary foundation. In answer to the first objection, Leibniz attempted to explain different orders of infinitesimals, pointing out that one could neglect all but the lowest orders in a given equation. To answer the second, he used the binomial theorem to demonstrate how to handle the differentials dx, dy, dz when y^x = z. To answer the third, Leibniz said that one should not think of d(dx) as a quantity that fails to yield a (finite) quantity even when multiplied by an infinite number. He pointed out that if x varies geometrically when y varies arithmetically—in modern terms, if x = e^y/a—then dx= (x dy)/a and ddx = (dx dy)/a, which makes perfectly good sense.

33.3 The Disciples of Newton and Leibniz

Newton and Leibniz had disciples who carried on their work. Among Newton's followers was Roger Cotes (1682–1716), who oversaw the publication of a later edition of Newton's Principia and defended Newton's inverse square law of gravitation in a preface to that work. He also fleshed out the calculus with some particular results on plane loci and considered the extension of functions defined by power series to complex values, deriving the important formula iϕ = log (cos ϕ + i sin ϕ), where . Another of Newton's followers was Brook Taylor (1685–1731), who developed a calculus of finite differences that mirrors in many ways the “continuous” calculus of Newton and Leibniz and is of both theoretical and practical use today. Taylor is famous for the infinite power series representation of functions that now bears his name. It appeared in his 1715 treatise on finite differences. We have already seen that many particular “Taylor series” were known to Newton and Leibniz; Taylor's merit is to have recognized a general way of producing such a series in terms of the derivatives of the generating function. This step, however, was also taken by Leibniz’ disciple John Bernoulli.

Leibniz also had a group of active and intelligent followers who continued to develop his ideas. The most prominent of these were the Bernoulli brothers James (1654–1705) and John (1667–1748), citizens of Switzerland, between whom relations were not always cordial. They investigated problems that arose in connection with calculus and helped to systematize, extend, and popularize the subject. In addition, they pioneered new mathematical subjects such as the calculus of variations, differential equations, and the mathematical theory of probability. A French nobleman, the Marquis de l'Hospital, took lessons from John Bernoulli and paid him a salary in return for the right to Bernoulli's mathematical discoveries. As a result, Bernoulli's discovery of a way of assigning values to what are now called indeterminate forms appeared in L’Hospital's 1696 textbook Analyse des infiniment petits(Infinitesimal Analysis) and has ever since been known as L’Hospital's rule. Like the followers of Newton, who had to answer the objections of Bishop Berkeley that will be discussed in the next section, Leibniz’ followers encountered objections from Michel Rolle (1652–1719), objections that were answered by John Bernoulli with the claim that Rolle didn't understand the subject.

33.4 Philosophical Issues

Some objections to the calculus were eloquently stated seven years after Newton's death by the philosopher George Berkeley⁵ (1685–1753, Anglican Bishop of Cloyne, Ireland), for whom the city of Berkeley⁶ in California is named. In his 1734 book The Analyst, Berkeley first took on Newton's fluxions, noting that “It is said that the minutest errors are not to be neglected in mathematics.”⁷ Berkeley continues:

[It is said] that the fluxions are celerities [speeds], not proportional to the finite increments, though ever so small; but only to the moments or nascent increments, whereof the proportion alone, and not the magnitude, is considered. And of the aforesaid fluxions there be other fluxions, which fluxions of fluxions are called second fluxions. And the fluxions of the second fluxions are called third fluxions: and so on, fourth, fifth, sixth, &c. ad infinitum. Now, as our sense is strained and puzzled with the perception of objects extremely minute, even so the imagination, which faculty derives from sense, is very much strained and puzzled to frame clear ideas of the least particles of time. . .and much more so to comprehend. . .those increments of the flowing quantities. . .in their very first origin, or beginning to exist, before they become finite particles. . .The incipient celerity of an incipient celerity, the nascent augment of a nascent augment, i.e., of a thing which hath no magnitude: take it in what light you please, the clear conception of it will, if I mistake not, be found impossible.

He then proceeded to attack the views of Leibniz:

The foreign mathematicians are supposed by some, even of our own, to proceed in a manner less accurate, perhaps, and geometrical, yet more intelligible. . .Now to conceive a quantity infinitely small, that is, infinitely less than any sensible or imaginable quantity or than any the least finite magnitude is, I confess, above my capacity. But to conceive a part of such infinitely small quantity that shall be still infinitely less than it, and consequently though multiplied infinitely shall never equal the minutest finite quantity, is, I suspect, an infinite difficulty to any man whatsoever.

Berkeley analyzed a curve whose area up to x was x³ (he wrote xxx). If z − x was the increment of the abscissa and z³ − x³ the increment of area, the quotient would be z² + zx + x². He said that, if z = x, of course this last expression is 3x², and that must be the ordinate of the curve in question. That is, its equation must be y = 3x². But, he pointed out,

[H]erein is a direct fallacy: for, in the first place, it is supposed that the abscisses z and x are unequal, without which supposition no one step could have been made [that is, the division by z − x would have been undefined]; which is a manifest inconsistency, and amounts to the same thing that hath been before considered. . .The great author of the method of fluxions felt this difficulty, and therefore he gave in to those nice abstractions and geometrical metaphysics without which he saw nothing could be done on the received principles. . .It must, indeed, be acknowledged that he used fluxions, like the scaffold of a building, as things to be laid aside or got rid of as soon as finite lines were found proportional to them. . .And what are these fluxions? The velocities of evanescent increments? And what are these same evanescent increments? They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities?

33.4.1 The Debate on the Continent

Calculus disturbed the metaphysical assumptions of philosophers and mathematicians on the Continent as well as in Britain. L’Hospital's textbook had made two explicit assumptions: first, that if a quantity is increased or diminished by a quantity that is infinitesimal in comparison with itself, it may be regarded as remaining unchanged. Second, that a curve may be regarded as an infinite succession of straight lines. L’Hospital's justification for these claims was not commensurate with the strength of the assumptions. He merely said:

[T]hey seem so obvious to me that I do not believe they could leave any doubt in the mind of attentive readers. And I could even have proved them easily after the manner of the Ancients, if I had not resolved to treat only briefly things that are already known, concentrating on those that are new. [Quoted by Mancosu, 1989, p. 228]

The idea that x + dx = x, implicit in l’Hospital's first assumption, leads algebraically to the equation dx = 0 if equations are to retain their previous meaning. Rolle raised this objection and was answered by the claim that dxrepresents the distance traveled in an instant of time by an object moving with finite velocity. This debate was carried on in private in the Paris Academy during the first decade of the eighteenth century, and members were at first instructed not to discuss it in public, as if it were a criminal case! Rolle's criticism could be answered, but it was not answered at the time. According to Mancosu (1989), the matter was settled in a most unacademic manner, by making l'Hospital into an icon after his death in 1704. His eulogy by Bernard Lebouyer de Fontenelle (1657–1757) simply declared the anti-infinitesimalists wrong, as if the Academy could decide metaphysical questions by fiat, just as it can define what is proper usage in French:

[T]hose who knew nothing of the mysteries of this new infinitesimal geometry were shocked to hear that there are infinities of infinities, and some infinities larger or smaller than others; for they saw only the top of the building without knowing its foundation. [Quoted by Mancosu (1989, 241)]

33.5 The Priority Dispute

One of the better known and less edifying incidents in the history of mathematics is the dispute between the disciples of Newton and those of Leibniz over the credit for the invention of the calculus. Although Newton had discovered the calculus by the early 1670s and had described it in a paper sent to James Collins, the librarian of the Royal Society, he did not publish his discoveries until 1687. Leibniz made his discoveries a few years later than Newton but published some of them earlier, in 1684. Newton's vanity was wounded in 1695 when he learned that Leibniz was regarded on the Continent as the discoverer of the calculus, even though Leibniz himself made no claim to this honor. In 1699 a Swiss immigrant to England, Nicolas Fatio de Duillier (1664–1753), suggested that Leibniz had seen Newton's paper when he had visited London and talked with Collins in 1673. (Collins died in 1683, before his testimony in the matter was needed.) This unfortunate rumor poisoned relations between Newton and Leibniz and their followers.

In 1711–1712 a committee of the Royal Society (of which Newton was President) investigated the matter and reported that it believed Leibniz had seen certain documents that in fact he had not seen. Relations between British and Continental mathematicians reached such a low ebb that Newton deleted certain laudatory references to Leibniz from the third edition of his Principia. This dispute confirmed the British in the use of the clumsy Newtonian notation for more than a century, a notation far inferior to the elegant and intuitive symbolism of Leibniz. But in the early nineteenth century the impressive advances made by Continental scholars such as Euler, Lagrange, and Laplace won over the British mathematicians. Scholars such as William Wallace (1768–1843) rewrote the theory of fluxions in terms of the theory of limits. Wallace asserted that there was never any need to introduce motion and velocity into this theory, except as illustrations, and that indeed Newton himself used motion only for illustration, recasting his arguments in terms of limits when rigor was needed [see Panteki (1987) and Craik 1999)]. Eventually, even the British began using the term integral instead of fluent and derivative instead of fluxion, and these Newtonian terms became mathematically part of a dead language.

Some important facts were obscured by the terms in which the priority dispute was cast. One of these is the extent to which Fermat, Descartes, Cavalieri, Pascal, Roberval, and others had developed the techniques in isolated cases that were to be unified by the calculus as we know it now. In any case, Newton's teacher Isaac Barrow had the insight into the connection between subtangents and area before either Newton or Leibniz thought of it. Barrow's contributions were ignored in the heat of the dispute; their significance has been pointed out by Feingold (1993).

33.6 Early Textbooks on Calculus

The secure place of calculus in the mathematical curriculum was established by the publication of a number of textbooks. One of the earliest was the Analyse des infiniment petits, mentioned above, which was published by the Marquis de l'Hospital in 1696.

Most students of calculus know the Maclaurin series as a special case of the Taylor series. Its discoverer was a Scottish contemporary of Taylor, Colin Maclaurin (1698–1746), whose Treatise of Fluxions (1742) contained a thorough and rigorous exposition of calculus. It was written partly as a response to Berkeley's attacks on the foundations of calculus.

The Italian textbook Istituzioni analitiche ad uso della gioventù italiana (Analytic Principles for the Use of Italian Youth) became a standard treatise on analytic geometry and calculus and was translated into English in 1801. Its author was Maria Gaetana Agnesi (1718–1799), one of the first women to achieve prominence in mathematics.

The definitive textbooks of calculus were written by the greatest mathematician of the eighteenth century, the Swiss scholar Leonhard Euler. In his 1748 Introductio in analysin infinitorum, a two-volume work, Euler gave a thorough discussion of analytic geometry in two and three dimensions, infinite series (including the use of complex variables in such series), and the foundations of a systematic theory of algebraic functions. The modern presentation of trigonometry was established in this work. The Introductio was followed in 1755 by Institutiones calculi differentialis and a three-volume Institutiones calculi integralis (1768–1774), which included the entire theory of calculus and the elements of differential equations, richly illustrated with challenging examples. It was in Euler's textbooks that many prominent nineteenth-century mathematicians such as the Norwegian genius Niels Henrik Abel (1802–1829) first encountered higher mathematics, and the influence of Euler's methods and results can be traced in their work.

33.6.1 The State of the Calculus Around 1700

Most of what we now know as calculus—rules for differentiating and integrating elementary functions, solving simple differential equations, and expanding functions in power series—was known by the early eighteenth century and was included in the standard textbooks just mentioned. Nevertheless, there was much unfinished work. We list here a few of the open questions:

1. Nonelementary Integrals. Differentiation of elementary functions is an algorithmic procedure, and the derivative of any elementary function whatsoever, no matter how complicated, can be found if the investigator has sufficient patience. Such is not the case for the inverse operation of integration. Many important elementary functions, such as (sin x)/x and , are not the derivatives of elementary functions. Since such integrals turned up in the analysis of some fairly simple motions, such as that of a pendulum, the problem of these integrals became pressing.

2. Differential Equations. Although integration had originally been associated with problems of area and volume, because of the importance of differential equations in mechanical problems the solution of differential equations soon became the major application of integration. The general procedure was to convert an equation to a form in which the derivatives could be eliminated by integrating both sides (reduction to quadratures). As these applications became more extensive, more and more cases began to arise in which the natural physical model led to equations that could not be reduced to quadratures. The subject of differential equations began to take on a life of its own, independent of the calculus.

3. Foundational Difficulties. The philosophical difficulties connected with the use of infinitesimal methods were paralleled by mathematical difficulties connected with the extension of the rules for operating with finite polynomials to infinite series. These difficulties were hidden for some time, and for a blissful century, mathematicians and physicists operated formally on power series as if they were finite polynomials. They did so even though it had been known since the time of Oresme that the partial sums of the harmonic series grow arbitrarily large.

Problems and Questions

Mathematical Problems

33.1 The mathematical structures called ordered fields, have most of the properties of real numbers, in the sense that one can add, subtract, multiply, and divide them, as well as compare any two of them to determine which is the larger. One such field is formed by the real-valued rational functions of a real variable, that is, quotients of polynomials with real coefficients, an example of which is

Two such functions and are regarded as equal if p(x)Q(x) = q(x)P(x) in the sense that the two sides are exactly the same polynomial, having exactly the same coefficients. Since polynomials have only a finite number of zeros, there is a largest zero for the numerator and denominator of a rational function . For values of x larger than that largest zero, the fraction is of constant sign. We define to mean that the values for all large x are positive, and to mean that .

Show that the rational function f(x) = x is positive and larger than any constant function g(x) = c. Then show that no finite number of divisions of f(x) by 2 will ever produce a function smaller than g(x). Hence the rational functions are a non-Archimedean ordered field. (The standard real numbers are an Archimedean ordered field.)

33.2 Show that the point at which the tangent to the curve y = f(x) intersects the y axis is (0, f(x) − xf' (x)), and verify that the area under the curve y = f(x) − xf' (x) from x = 0 to x = a is twice the area between the curve y = f(x) and the line ay = f(a)x. This result was used by Leibniz to illustrate the power of his infinitesimal methods.

33.3 The principle that a curve is closely approximated by its tangent line at points near the point of tangency accounts for both the existence and the usefulness of the derivative. While the curve may have such a complicated equation that computations involving it are not feasible, the tangent line is computable, and computations on the tangent line involve only first-degree equations. That is the basis of Newton's method of approximating points where a function f(x) is zero. You make a guess x₀, compute the tangent line at the point (x₀, f(x₀)), which has equation y − f(x₀) = f' (x₀)(x − x₀), and solve it for x when y = 0, getting a new guess x₁, which one can hope is an improvement:

If x₁ still isn't good enough, repeat the process to get x₂, and so on.

Use this technique to find . That is, find a zero of the function f(x) = x² − 2, for which f' (x) = 2x, starting with the guess x₀ = 2. What sequence of approximations do you obtain? How close is x₄ to ?

Historical Questions

33.4 When did Newton begin to create the calculus, and what problems did he solve with it?

33.5 When did Leibniz begin to create the calculus, and what may have been his motive for doing so?

33.6 What were the objections that philosophers raised against the techniques of calculus?

Questions for Reflection

33.7 Just as Eudoxus solved the problem of incommensurables by making a definition of proportion to cover cases where no definition existed before, Newton's “theorem” asserting that quantities that approach each other monotonically and become arbitrarily close to each other in a finite time must become equal in an infinite time assumes that one has a definition of equality at infinity. Formulate such a definition.

33.8 Draw a square and one of its diagonals. Then draw a very fine “staircase” by connecting short horizontal and vertical line segments in alternation, each segment crossing the diagonal. The total length of the horizontal segments is the same as the side of the square, and the same is true of the vertical segments, so that the total length of these segments is twice the length of a side. In an intuitive sense these segments do approximate the diagonal of the square, since they get closer and closer to it as the number of steps increases. This fact seems to imply that the diagonal of a square equals twice its side, which is absurd. Does this argument show that the method of indivisibles is wrong?

33.9 In the passage quoted from the Analyst, Berkeley asserts that the experience of the senses provides the only foundation for our imagination. From that premise he concludes that we can have no understanding of infinitesimals. Analyze whether the premise is true, and if so, whether it implies the conclusion. Assuming that our thinking processes have been shaped by the evolution of the brain, for example, is it possible that some of our spatial and counting intuition is “hard-wired” and not the result of any previous sense impressions? The philosopher Immanuel Kant (1724–1804) thought so. Do we have the power to make correct judgments about spaces and times on scales that we have not experienced? What would Berkeley have said if he had heard Riemann's argument that space may be finite, yet unbounded? If our intuition is “hard-wired,” does it follow that it is a perfectly accurate reflection of reality?

Notes

1. The vertical axis is to be assumed positive in both directions from the origin. We are preserving in Fig. 33.1 only the lines needed to explain Leibniz’ argument. He himself merely labeled points on the two curves with letters and referred to those letters.

2. The limits of integration shown here were unknown in Leibniz’ time. They were introduced in the nineteenth century by Joseph Fourier (1768–1830).

3. Bernard Nieuwentijt (1654–1718) was a Dutch Calvinist theologian.

4. This principle was set forth as fundamental in the following year in the textbook of calculus by the Marquis de l'Hospital (1661–1704).

5. Pronounced “Barkley.”

6. Pronounced “Birkley.”

7. It was indeed said, and by Newton himself, in his 1704 treatise Introduction to the Quadrature of Curves.