The history of mathematics: A brief course (2013)
Part VI. European Mathematics, 500-1900
Chapter 34. Consolidation of the Calculus
The calculus grew organically, sending forth branches while simultaneously putting down roots. The roots were the subject of philosophical speculation that eventually led to new mathematics as well, but the branches were natural outgrowths of pure mathematics that appeared very early in the history of the subject. In order to carry the story to a natural conclusion, we shall go beyond the time limits we have set for ourselves in this part and discuss results from the nineteenth century, but only in relation to calculus (analysis). The development of modern algebra, number theory, geometry, probability, and other subjects will be discussed in later chapters. In addition to the pioneers of calculus we have already discussed, we will be mentioning a number of outstanding eighteenth-and nineteenth-century mathematicians who made contributions to analysis, especially the following:
1. Leonhard Euler (1707–1783), a Swiss mathematician who became one of the early members of the Russian Academy of Sciences (1727–1741), then spent a quarter-century in Berlin (1741–1766) before returning to St. Petersburg when the Prussian Princess Catherine II (1762–1796) ruled there. He holds the record for having written the greatest volume of mathematical papers in all of history, amounting to more than 80 large volumes in the edition of his collected works. (A mathematician whose works fill 10 volumes is an extreme rarity.)
2. Jean le Rond d'Alembert (1717–1783), a French mathematician who made significant contributions to algebra, in which he attempted to prove that every polynomial with real coefficients can be written as a product of linear and quadratic factors with real coefficients. (If he had succeeded, he would as a by-product have proved the fundamental theorem of algebra.) He also contributed to partial differential equations (the vibrating string problem) and the foundations of mathematics. He was one of the authors of the great compendium of knowledge known as the Encyclopédie.
3. Joseph-Louis Lagrange (1736–1813), an Italian mathematician (Giuseppe-Luigi Lagrange), who spent most of his life in Berlin and Paris. He worked on many of the same problems in analysis as Euler. These two were remarkably prolific and between them advanced analysis, mechanics, and algebra immensely. Lagrange represented an algebraic point of view in analysis, generally eschewing appeals to geometry.
4. Adrien-Marie Legendre (1752–1833), a French mathematician who founded the theory of elliptic functions and made fundamental contributions to number theory. He also was one of the earliest to recognize the importance of least-squares approximation.
5. Augustin-Louis Cauchy (1789–1856), the most prolific mathematician of the nineteenth century. He published constantly in the Comptes rendus (Reports) of the Paris Academy of Sciences. He raised the level of rigor in real analysis and was largely responsible for shaping one of three basic approaches to complex analysis. Although we shall be discussing some particular results of Cauchy in connection with the solution of algebraic and differential equations, his treatises on analysis are the contributions for which he is best remembered. He became a mathematician only after practicing as an engineer for several years.
6. Carl Gustav Jacob Jacobi (1804–1851), the first Jewish professor in Germany, who worked in many areas, including mechanics, elliptic and more general algebraic functions, differential equations, and number theory.
7. Karl Weierstrass (1815–1897), a professor at the University of Berlin from 1855 until his death. His insistence on clarity led him to reformulate much of analysis, algebra, and calculus of variations.
8. Bernhard Riemann (1826–1866), a brilliant geometer at the University of Göttingen. In frail health (he died young, of tuberculosis), he applied his wonderful intuition to invent a geometric style in complex analysis and algebra that complemented the analytic style of Weierstrass and the algebraic style of the Lagrangian tradition.
In our examination of the tree of calculus, we begin with the branches and will end with the roots.
34.1 Ordinary Differential Equations
Ordinary differential equations arose almost as soon as there was a language (differential calculus) in which they could be expressed. These equations were used to formulate problems from geometry and physics in the late seventeenth century, and the natural approach to solving them was to apply the integral calculus, that is, to reduce a given equation to quadratures. Leibniz, in particular, developed the technique now known as separation of variables as early as 1690 (Grosholz, 1987). In the simplest case, that of an ordinary differential equation of first order and first degree, one is seeking an equation f(x, y) = c, which may be interpreted as a conservation law if x and y are functions of time having physical significance. The conservation law is expressed as the differential equation
![]()
The resulting equation is known as an exact differential equation, since the left-hand side is the exact differential of the function f(x, y). To solve this equation, one has only to integrate the first differential with respect to x, adding an arbitrary function g(y) to the solution, then differentiate with respect to y and compare the result with ![]() in order to get an equation for g'(y), which can then be integrated.
in order to get an equation for g'(y), which can then be integrated.
If all equations were this simple, differential equations would be a very trivial subject. Unfortunately, it seems that nature tries to confuse us, multiplying these equations by arbitrary functions μ(x, y). That is, when an equation is written down as a particular case of a physical law, it often looks like
![]()
where ![]() and
and ![]() , and no one can tell from looking at M just which factors in it constitute μ and which constitute
, and no one can tell from looking at M just which factors in it constitute μ and which constitute ![]() . To take the simplest possible example, the mass y of a radioactive substance that remains undecayed in a sample after time x satisfies the equation
. To take the simplest possible example, the mass y of a radioactive substance that remains undecayed in a sample after time x satisfies the equation
![]()
where k is a constant. The mathematician's job is to get rid of μ(x, y) by looking for an “integrating factor” that will make the equation exact.1 One integrating factor for this equation is 1/y; another is e−kx. (When the equation is solved, these are seen to be the same function.)
It appeared at a very early stage that finding an integrating factor is not in general possible, and both Newton and Leibniz were led to the use of infinite series with undetermined coefficients to solve such equations. Later, Maclaurin, was to warn against too hasty recourse to infinite series, saying that certain integrals could be better expressed geometrically as the arc lengths of various curves. But the idea of replacing a differential equation by a system of algebraic equations was very attractive. The earliest examples of series solutions were cited by Feigenbaum (1994). In his Fluxions, Newton considered the linear differential equation that we would now write as
![]()
Newton wrote it as n/m = 1 − 3x + y + xx + xy and found that
![]()
Similarly, in a paper published in the Acta eruditorum in 1693 (Gerhardt, 1971, Vol. 5, p. 287), Leibniz studied the differential equations for the logarithm and the arcsine in order to obtain what we now call the Maclaurin series of the logarithm, exponential, and sine functions. For example, he considered the equation a2 dy2 = a2 dx2 + x2 dy2 and assumed that x = by+ cy3 + ey5 + fy7 + ![]() , thereby obtaining the series that represents the function x = a sin (y/a). Neither Newton nor Leibniz mentioned that the coefficients in these series were the derivatives of the functions represented by the series divided by the corresponding factorials. However, that realization came to John Bernoulli very soon after the publication of Leibniz’ work. In a letter to Leibniz dated September 2, 1694 (Gerhardt, 1971, Vol. 3/1, p. 350), Bernoulli described essentially what we now call the Taylor series of a function. In the course of this description, he gave in passing what became a standard definition of a function, saying, “I take n to be a quantity formed in an arbitrary manner from variables and constants.” Leibniz had used the word function as early as 1673, and in an article in the 1694 Acta eruditorum had defined a function to be “the portion of a line cut off by lines drawn using only a fixed point and a given point lying on a curved line.” As Leibniz said, a given curve defines a number of functions: its abscissas, its ordinates, its subtangents, and so on. The problem that differential equations solve is to reconstruct the curve given the ratio between two of these functions.2
, thereby obtaining the series that represents the function x = a sin (y/a). Neither Newton nor Leibniz mentioned that the coefficients in these series were the derivatives of the functions represented by the series divided by the corresponding factorials. However, that realization came to John Bernoulli very soon after the publication of Leibniz’ work. In a letter to Leibniz dated September 2, 1694 (Gerhardt, 1971, Vol. 3/1, p. 350), Bernoulli described essentially what we now call the Taylor series of a function. In the course of this description, he gave in passing what became a standard definition of a function, saying, “I take n to be a quantity formed in an arbitrary manner from variables and constants.” Leibniz had used the word function as early as 1673, and in an article in the 1694 Acta eruditorum had defined a function to be “the portion of a line cut off by lines drawn using only a fixed point and a given point lying on a curved line.” As Leibniz said, a given curve defines a number of functions: its abscissas, its ordinates, its subtangents, and so on. The problem that differential equations solve is to reconstruct the curve given the ratio between two of these functions.2
In classical terms, the solution of a differential equation is a function or family of functions. Given that fact, the ways in which a function can be presented become an important issue. With the modern definition of a function and the familiar notation, one might easily forget that in order to apply the theory of functions it is necessary to deal with particular functions, and these must be presented somehow. Bernoulli's description addresses that issue, although it leaves open the question of what methods of combining variables and constants are legal.
34.1.1 A Digression on Time
The Taylor series of a given function can be generated knowing the values of the function over any interval of the independent variable, no matter how short. Thus, a quantity represented by such a series is determined for all values of the independent variable when the values are given on any interval at all. Given that the independent variable is usually time, that property corresponds to physical determinacy: Knowing the full state of a physical quantity for some interval of time determines its values for all time. Lagrange, in particular, was a proponent of power series, for which he invented the term analytic function. However, as we now know, the natural domain of analytic function theory is the complex numbers. Now in mechanics the independent variable often represents time, and that fact raises an interesting question: Why should time be a complex variable? How do complex numbers turn out to be relevant to a problem where only real values of the variables have any physical meaning? To this question the eighteenth-and nineteenth-century mathematicians gave no answer. Indeed, it does not appear that they even asked the question very often. Extensive searches of the nineteenth-century literature by the present author have produced only the following comments on this interesting question, made by Weierstrass in 1885 (see his Werke, Bd. 3, S. 24):
It is very remarkable that in a problem of mathematical physics where one seeks an unknown function of two variables that, in terms of their physical meaning, can have only real values and is such that for a particular value of one of the variables the function must equal a prescribed function of the other, an expression often results that is an analytic function of the variable and hence also has a meaning for complex values of the latter.
It is indeed very remarkable, but neither Weierstrass nor anyone since seems to have explained the mystery. Near the end of Weierstrass' life, Felix Klein (1897) remarked that if physical variables are regarded as complex, a rotating rigid body can be treated either as a motion in hyperbolic space or motion in Euclidean space accompanied by a strain. Perhaps, since they had seen that complex numbers were needed to produce the three real roots of a cubic equation, it may not have seemed strange to them that the complex-variable properties of solutions of differential equations are relevant in the study of problems generated by physical considerations involving only real variables. Time is sometimes represented as a two-dimensional quantity in connection with what are known as Gibbs random fields.
34.2 Partial Differential Equations
In the middle of the eighteenth century mathematical physicists began to consider problems involving more than one independent variable. The most famous of these is the vibrating string problem discussed by Euler, d'Alembert, and Daniel Bernoulli (1700–1782, son of John Bernoulli) during the 1740s and 1750s.3 This problem led to the one-dimensional wave equation
![]()
with the initial conditions u(x, 0) = f(x), ![]() . Here u(x, t) is the height of the point of the string above x at time t. Daniel Bernoulli solved this equation in the form of an infinite double trigonometric series
. Here u(x, t) is the height of the point of the string above x at time t. Daniel Bernoulli solved this equation in the form of an infinite double trigonometric series
![]()
claiming that the an could be chosen so that ![]() . This solution was criticized by Euler, leading to a debate over the allowable methods of defining functions and the proper definition of a function.
. This solution was criticized by Euler, leading to a debate over the allowable methods of defining functions and the proper definition of a function.
The developments that grew out of trigonometric-series techniques like this one by Daniel Bernoulli will be discussed in Chapter 42, along with the development of real analysis in general. For the rest of the present section, we confine our discussion to power-series techniques of solving partial differential equations.
In the nineteenth century, Newton's power-series method was applied to the heat equation
![]()
by Joseph Fourier, who is actually better known for applying trigonometric series and integrals in such cases. (In fact, they are called Fourier series and integrals in his honor.) In this equation, u(x, t) represents the temperature at time t at point x in a long thin wire. Assuming that the temperature at x at time t = 0 is ϕ(x) and a = 1, Fourier obtained the solution
![]()
As it turns out, this series often diverges for all nonzero values of t.
It was not until the nineteenth century that mathematicians began to worry about the convergence of series solutions. First Cauchy, and then Weierstrass produced proofs that the series do converge for ordinary differential equations, provided that the coefficients have convergent series representations. For partial differential equations, between 1841 and 1876, Cauchy, Jacobi, Weierstrass, Weierstrass' student Sof'ya Kovalevskaya (1850–1891), and Gaston Darboux (1842–1917), produced theorems that guaranteed convergence of the formally generated power series. In general, however, it turned out that the series formally satisfying the equation could actually diverge, and that the algebraic form of the equation controlled whether it did or not. Kovalevskaya showed that in general the power series solution for the heat equation diverges if the initial temperature distribution is prescribed, even when that temperature is an analytic function of position. (This is the case considered by Fourier.) She showed, however, that the series converges if the temperature and temperature gradient at one point are prescribed as analytic functions of time. More generally, she showed that the power-series solution of any initial-value problem in “normal form” would converge. Normal form is relative to a particular variable that occurs in the equation. It means that the initial conditions are imposed on a variable whose highest-order pure derivative in the equation equals the order of the equation. The heat equation is in normal form relative to the spatial variable, but not relative to the time variable.
34.3 Calculus of Variations
The notion of function lies at the heart of calculus. The usual picture of a function is of one point being mapped to another point. However, the independent variable in a function can be a curve or surface as well as a point. For example, given a curve γ that is the graph of a function y = f(x) between x = a and x = b, we can define its length as
![]()
One of the important problems in the history of geometry has been to pick out the curve γ that minimizes Λ(γ) and satisfies certain extra conditions, such as joining two fixed points P and Q on a surface or enclosing a fixed area A. The calculus technique of “setting the derivative equal to zero” needs to be generalized for such problems, and the techniques for doing so constitute the calculus of variations. The history of this outgrowth of the calculus has been studied in many classic works, such as those by Woodhouse (1810),4 Todhunter (1861), and Goldstine (1980), and in articles like the one by Kreyszig (1993).
As with the ordinary calculus, the development of calculus of variations proceeded from particular problems solved by special devices to general techniques and algorithms based on theoretical analysis and rigorous proof. In the seventeenth century there were three such special problems that had important consequences. The first was the brachistochrone (shortest-time) problem for an object crossing an interface between two media while moving from one point to another. In the simplest case (Fig. 34.1), the interface is a straight line, and the time required to travel from P to Q at speed ![]() above the line P0Q0 and speed
above the line P0Q0 and speed ![]() below it is to be minimized. If the two speeds are not the same, it is clear that the path of minimum time will not be a straight line, since time can be saved by traveling a slightly longer distance in the medium in which the speed is greater. The path of minimum time turns out to be the one in which the sines of the angle of incidence and refraction have a fixed ratio, namely the ratio of the speeds in the two media. (Compare this result with the shortest reflected path in a single medium, discussed in Problem 15.1 of Chapter 15, which is also a path of minimum time.)
below it is to be minimized. If the two speeds are not the same, it is clear that the path of minimum time will not be a straight line, since time can be saved by traveling a slightly longer distance in the medium in which the speed is greater. The path of minimum time turns out to be the one in which the sines of the angle of incidence and refraction have a fixed ratio, namely the ratio of the speeds in the two media. (Compare this result with the shortest reflected path in a single medium, discussed in Problem 15.1 of Chapter 15, which is also a path of minimum time.)
Figure 34.1 Left: Fermat's principle. The time of travel from P to Q is a minimum if the ray crosses the interface at the point where ![]() . Right: Application of this principle to the brachistochrone, assuming the speed varies continuously in proportion to the square root of the distance of descent.
. Right: Application of this principle to the brachistochrone, assuming the speed varies continuously in proportion to the square root of the distance of descent.
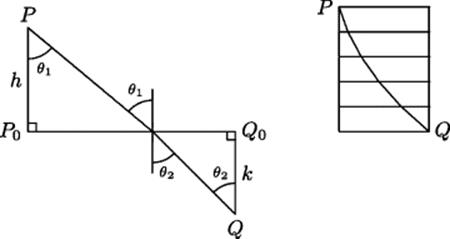
Fermat's principle, which asserts that the path of a light ray is the one that requires least time, found application in the second problem, stated as a challenge by John Bernoulli in 1696: Find the curve down which a frictionless particle will slide from point P to point Q under the influence of gravity in minimal time. Since the speed of a falling body is proportional to the square root of the distance fallen, Bernoulli reasoned that the sine of the angle between the tangent and the vertical would be proportional to the square root of the vertical coordinate, assuming the vertical axis directed downward.5 In that way, Bernoulli arrived at a differential equation for the curve:
![]()
Here we have taken y as the vertical coordinate, directed downward. He recognized this equation as the differential equation of a cycloid and thus concluded that this curve, which Christiaan Huygens (1629–1695) had studied because it enabled a clock to keep theoretically perfect time (the tautochrone property, discussed in Chapter 39), also had the brachistochrone property. The challenge problem was solved by Bernoulli himself, by his brother James, and by both Newton and Leibniz.6 According to Woodhouse (1810, p. 150), Newton's anonymously submitted solution was so concise and elegant that John Bernoulli knew immediately who it must be from. He wrote, “Even though the author, from excessive modesty, does not give his name, we can nevertheless tell certainly by a number of signs that it is the famous Newton; and even if these signs were not present, seeing a small sample would suffice to recognize him, as ex ungue Leonem.”7
The third problem, that of finding the cross-sectional shape of the optimally streamlined body moving through a resisting medium, is discussed in the scholium to Proposition 34 (Theorem 28) of Book 2 of Newton's Principia.
34.3.1 Euler
Variational problems were categorized and systematized by Euler in a large treatise in 1744 named Methodus inveniendi lineas curvas (A Method of Finding Curves). In this treatise Euler set forth a series of problems of increasing complexity, each involving the finding of a curve having certain extremal properties, such as minimal length among all curves joining two points on a given surface.8 Proposition 3 in Chapter 2, for example, asks for the minimum value of an integral ∫Z dx, where Z is a function of variables, x, y, and ![]() . Based on his previous examples, Euler derived the differential equation
. Based on his previous examples, Euler derived the differential equation
![]()
where dZ = M dx + N dy + P dp is the differential of the integrand Z. Since ![]() and
and ![]() , this equation could be written in the form that is now the basic equation of the calculus of variations, and is known as Euler's equation:
, this equation could be written in the form that is now the basic equation of the calculus of variations, and is known as Euler's equation:
![]()
In Chapter 3, Euler generalized this result by allowing Z to depend on additional parameters and applied his result to find minimal surfaces. In an appendix he studied elastic curves and surfaces, including the problem of the vibrating membrane. This work was being done at the very time when Euler's former colleague Daniel Bernoulli was studying the simpler problem of the vibrating string. In a second appendix, Euler showed how to derive the equations of mechanics from variational principles, thus providing a unifying mathematical principle that applied to both optics (Fermat's principle) and mechanics.9
34.3.2 Lagrange
The calculus of variations acquired “variations” and its name as the result of a letter written by Lagrange to Euler in 1755. In that letter, Lagrange generalized Leibniz’ differentials from points to curves, using the Greek δ instead of the Latin d to denote them. Thus, if y = f(x) was a curve, its variation δy was a small perturbation of it. Just as dy was a small change in the value of y at a point, δy was a small change in all the values of y at all points. The variation operator δ can be manipulated quite easily, since it commutes with differentiation and integration: δy' = (δy)' and δ ∫ Z dx = ∫ δZ dx. With this operator, Euler's equation and its many applications were easy to derive. Euler recognized the usefulness of what Lagrange had done and gave the new theory the name it has borne ever since: calculus of variations.
Lagrange also considered extremal problems with constraint and introduced the famous Lagrange multipliers as a way of turning these relative (constrained) extrema into absolute (unconstrained) extrema. Euler had given an explanation of this process earlier. Woodhouse (1810, p. 79) thought that Lagrange's systematization actually deprived Euler's ideas of their simplicity.
34.3.3 Second-Variation Tests for Maxima and Minima
Like the equation f' (x) = 0 in calculus, the Euler equation is only a necessary condition for an extremal, not sufficient, and it does not distinguish between maximum, minimum, and neither. In general, however, if Euler's equation has only one solution, and there is good reason to believe that a maximum or minimum exists, the solution of the Euler equation provides a basis to proceed in practice. Still, mathematicians were bound to explore the question of distinguishing maxima from minima. Such investigations were undertaken by Lagrange and Legendre in the late eighteenth century.
In 1786 Legendre was able to show that a sufficient condition for a minimum of the integral
![]()
at a function satisfying Euler's necessary condition, was ![]() for all x and that a sufficient condition for a maximum was
for all x and that a sufficient condition for a maximum was ![]() .
.
In 1797 Lagrange published a comprehensive treatise on the calculus, in which he objected to some of Legendre's reasoning, noting that it assumed that certain functions remained finite on the interval of integration (Dorofeeva, 1998, p. 209).
34.3.4 Jacobi: Sufficiency Criteria
The second-variation test is strong enough to show that a solution of the Euler equation really is an extremal among the smooth functions that are “nearby” in the sense that their values are close to those of the solution and their derivatives also take values close to those of the derivative of the solution. Such an extremal was called a weak extremal by Adolf Kneser (1862–1930). Jacobi had the idea of replacing the curve y(x) that satisfied Euler's equation with a family of such curves depending on parameters (two in the case we have been considering) y(x, α1, α2) and replacing the nearby curves y + δy and y' + δy' with values corresponding to different parameters. In 1837—see Dorofeeva (1998) or Fraser (1993)—he finally solved the problem of finding sufficient conditions for an extremal. He included his solution in the lectures on dynamics that he gave in 1842, which were published in 1866, after his death. The complication that had held up Jacobi and others was the fact that sometimes the extremals with given endpoints are not unique. The most obvious example is the case of great circles on the sphere, which satisfy the Euler equations for the integral that gives arc length subject to fixed endpoints. If the endpoints happen to be antipodal points, all great circles passing through the two points have the same length. Weierstrass was later to call such pairs of points conjugate points. Jacobi gave a differential equation whose solutions had zeros at these points and showed that Legendre's criterion was correct, provided that the interval (a, b] contained no points conjugate to a.
34.3.5 Weierstrass and his School
A number of important advances in the calculus of variations were due to Weierstrass, such as the elimination of some of the more restrictive assumptions about differentiability and taking account of the distinction between a lower bound and a minimum.10
An important example in this connection was Riemann's use of Dirichlet's principle to prove the Riemann mapping theorem, which asserts that any simply connected region in the plane except the plane itself can be mapped conformally onto the unit disk Δ = {(x, y) : x2 + y2 < 1}. That principle required the existence of a real-valued function u(x, y) that minimizes the integral
![]()
among all functions u(x, y) taking prescribed values on the boundary of the disk. That function is the unique harmonic function11 in Δ with the given boundary values. In 1870, Weierstrass called attention to the integral
![]()
which when combined with the boundary condition ϕ(− 1) = a, ϕ(+ 1) = b, can be made arbitrarily small by taking k sufficiently large in the formula
![]()
yet (if a ≠ b) cannot be zero for any function ϕ satisfying the boundary conditions and such that ϕ' exists at every point.
Weierstrass' example was a case where it was necessary to look outside the class of smooth functions for a minimum of the functional. The limiting position of the graphs of the functions for which the integral approximates its minimum value consists of the two horizontal lines from (− 1, a) to (0, a), from (0, b) to (+ 1, b), and the section of the y-axis joining them (see Fig. 34.2).
Figure 34.2 The functional ![]() does not assume its minimum value for continuously differentiable functions y(x) satisfying y(− 1) = 2, y(+ 1) = 4. The limiting position of a minimizing sequence is the dashed line.
does not assume its minimum value for continuously differentiable functions y(x) satisfying y(− 1) = 2, y(+ 1) = 4. The limiting position of a minimizing sequence is the dashed line.
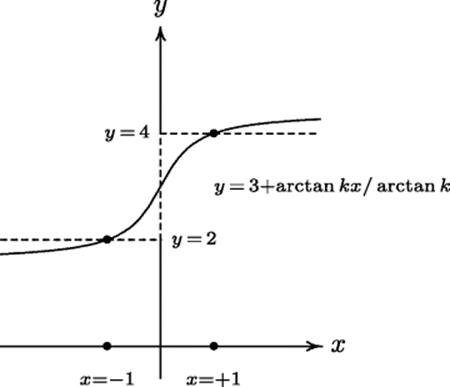
Weierstrass thought of the smoothness assumptions as necessary evils. He recognized that they limited the generality of the results, yet he saw that without them no application of the calculus was possible. The result is a certain vagueness about the formulation of minimal principles in physics. A certain functional must be a minimum assuming that all the relevant quantities are differentiable a sufficient number of times. Obviously, if a functional can be extended to a wider class of functions in a natural way, the minimum reached may be smaller, or the maximum larger. To make the restrictions as weak as possible, Weierstrass imposed the condition that the partial derivatives of the integrand should be continuous at corners. An extremal among all functions satisfying these less restrictive hypotheses was called a strong extremal. The corner condition was also found in 1877 by G. Erdmann (dates unknown), a teacher at the Gymnasium in Königsberg, who proved in 1878 that Jacobi's sufficient condition for a weak extremal was also necessary.
34.4 Foundations of the Calculus
The British and Continental mathematicians both found the power of the calculus so attractive that they applied and developed it (sending forth new branches), all the while struggling to be clear about the principles they were using (extending its roots). The branches grew more or less continuously from the beginning. The development of the roots was slower and more sporadic. A satisfactory consensus was achieved only late in the nineteenth century, with the full development of real analysis.
The source of the difficulty was the introduction of the infinite into analysis in the form of infinitesimal reasoning. As mentioned in the previous chapter, Leibniz believed in actual infinitesimals, levels of magnitude that were real, not zero, but so small that no accumulation of them could ever exceed any finite quantity. His dx was such an infinitesimal, and a product of two, such as dx dy or dx2, was a higher-order infinitesimal, so small that no accumulation of such could ever exceed any infinitesimal of the first order. On this view, even though theorems established using calculus were not absolutely accurate, the errors were below the threshold of human perception and therefore could not matter in practice. Newton was probably alluding to this belief of Leibniz when, in his discussion of the quadrature of curves (1704), he wrote, “In rebus mathematicis errores quam minimi non sunt contemnendi” (“Errors, no matter how small, are not to be allowed in mathematics”).12
Newton knew that his arguments could have been phrased using the Eudoxan method of exhaustion. In his Principia he wrote that he used his method of first and last ratios “to avoid the tediousness of deducing involved demonstrations ad absurdum, according to the method of the ancient geometers.” That is to say, to avoid the trichotomy arguments used by Archimedes.
There seemed to be three approaches that would allow the operation that we now know as integration to be performed by antidifferentiation of tangents. One is the infinitesimal approach of Leibniz, characterized by Mancosu (1989) as “static.” That is, a tangent is a state or position of a line, namely that of passing through two infinitely near points. The second is Newton's “dynamic” approach, in which a fluxion is the velocity of a moving object. The third is the ancient method of exhaustion. In principle, a reduction of calculus to the Eudoxan theory of proportion is possible. Psychologically, it would involve not only a great deal of tedium, as Newton noted, but also a great deal of confusion. If mathematicians had been shackled by the requirements of this kind of rigor, the amount of geometry and analysis created would have been much smaller than it was.
In the eighteenth century, however, better expositions of the calculus were produced by d'Alembert and others. In his article on the differential for the famous Encyclopédie, d'Alembert wrote that 0/0 could be equal to anything, and that the derivative ![]() was not actually 0 divided by 0, but the limit of finite quotients as numerator and denominator tended to zero. (This was essentially what Newton had said in his Principia.)
was not actually 0 divided by 0, but the limit of finite quotients as numerator and denominator tended to zero. (This was essentially what Newton had said in his Principia.)
34.4.1 Lagrange's Algebraic Analysis
The attempt to be clear about infinitesimals or to banish them entirely took many forms during the eighteenth and nineteenth centuries. One of them (see Fraser, 1987) was Lagrange's exposition of analytic functions. Lagrange understood the term function to mean a formula composed of symbols representing variables and arithmetic operations. He argued that “in general” (with certain obvious exceptions) every function f(x) could be expanded as a power series, based on Taylor's theorem, for which he provided his own form of the remainder term. He claimed that the hypothetical expansion
![]()
could not occur, since the left-hand side has only two values, while the right-hand side has n values.13 In this way, he ruled out fractional exponents. Negative exponents were ruled out by the mere fact that the function was defined at h = 0. The determinacy property of analytic functions was used implicitly by Lagrange when he assumed that any zero of a function must have finite order, as we would say (Fraser, 1987, p. 42).
The advantage of confining attention to functions defined by power series is that the derivative and integral of such a function have a perfectly definite meaning. Lagrange advocated it on the grounds that it showed the qualitative difference between the functions dx and x.
34.4.2 Cauchy's Calculus
The modern presentation of calculus owes a great deal to the textbooks of Cauchy, written for his lectures at the Ecole Polytechnique during the 1820s. Cauchy recognized that calculus could not get by without something equivalent to infinitesimals. He defined a function f(x) to be continuous if the absolute value of the difference f(x + α) − f(x) “decreases without limit along with that of α.” He continues:
In other words, the function f(x) remains continuous with respect to x in a given interval, if an infinitesimal increase in the variable within this interval always produces an infinitesimal increase in the function itself.
Cauchy did not discuss the question whether only one single point x is being considered or the increase is being thought of as occurring at all points simultaneously. It turns out that the size of the infinitesimal change in f(x) corresponding to a given change in x may vary from one point to another and from one function to another. Stronger assumptions, invoking the concepts of uniform continuity and equicontinuity are needed to guarantee results such as Cauchy stated here. In particular, he uniform convergence and continuity but did not say so. Cauchy defined a limit in terms of the “successive values attributed to a variable,” approaching a fixed value and ultimately differing from it by an arbitrarily small amount. This definition can be regarded as an informal version of what we now state precisely with deltas and epsilons; and Cauchy is generally regarded, along with Weierstrass, as one of the people who finally made the foundations of calculus secure. Yet Cauchy's language clearly presumes that infinitesimals are real. As Laugwitz (1987, p. 272) says:
All attempts to understand Cauchy from a ‘rigorous' theory of real numbers and functions including uniformity concepts have failed. . .One advantage of modern theories like the Nonstandard Analysis of Robinson. . . [which includes infinitesimals] is that they provide consistent reconstructions of Cauchy's concepts and results in a language which sounds very much like Cauchy's.
The secure foundation of modern analysis owes much to Cauchy's treatises. As Grabiner (1981) said, he applied ancient Greek rigor and modern algebraic techniques to derive results from analysis.
Problems and Questions
Mathematical Problems
34.1 Consider the one-dimensional heat equation, according to which the temperature u at point x along a line (say a wire) at time t satisfies
![]()
where k is a constant of proportionality. Assume the units of time and distance are chosen so that k = 1. If the initial temperature distribution is given by the so-called witch of Agnesi14 u(x, 0) = (1 + x2)−1 (so that the temperature has some resemblance to a bell-shaped curve), assume that
![]()
Use the fact that
![]()
for all small x to conclude that
![]()
Then differentiate formally, and show that the assumed series for u(x, t) must be
![]()
Show that this series diverges for all nonzero values of t when x = 0.
34.2 There are yet more subtleties in the notion of continuity than even Cauchy realized. In one of his works, he had stated the theorem that the sum of a series of continuous functions is continuous. Abel, who admired Cauchy's mathematics (while regarding Cauchy himself as rather crazy), diplomatically pointed out that “this theorem appears to admit some exceptions.” In fact,
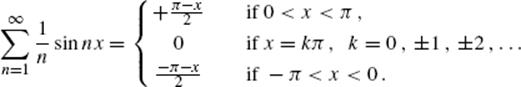
Since Cauchy had argued that an infinitesimal change in x will produce an infinitesimal change in each term ![]() , why does an infinitesimal increase in x starting at x = 0 not produce an infinitesimal change in the sum of this series?
, why does an infinitesimal increase in x starting at x = 0 not produce an infinitesimal change in the sum of this series?
34.3 Fill in the details of Weierstrass' example of a functional that does not assume its minimum value subject to certain endpoint conditions. In Fig. 34.2, the function yk = 3 + arctan (kx)/arctan (k) satisfies the endpoint conditions that y(− 1) = 2 and y(+ 1) = 4. Using partial fractions to do the integration, you can show that
![]()
which obviously tends to zero as k→ ∞. For the functional actually to be zero, however, y' (x) would have to be identically zero except at x = 0, and so y(x) would have to be 2 for x < 0 and 4 for x > 0.
Historical Questions
34.4 How does the calculus of variations differ from ordinary calculus?
34.5 What new methodological questions arose in the course of solving the problem of the vibrating string?
34.6 What solutions did nineteenth-century analysts like Cauchy and Weierstrass find to the philosophical difficulties connected with infinitesimals?
Questions for Reflection
34.7 Is it possible to make calculus “finitistic,” so that each step in its development refers only to a finite number of concrete things? Or is the infinite inherent in the subject? In particular, does Lagrange's approach, developing functions as power series and defining the derivative as the coefficient of the first-degree term, satisfy such a requirement and eliminate the need for infinitesimals?
34.8 What sense can you make out of time as a complex variable? If it has no meaning at all, why did Weierstrass and his students think it important to use complex variables in solving differential equations?
34.9 What differences are there between an algebraic equation and a differential equation? What does the term solution mean for each of them?
Notes
1. The equations presented in first courses on differential equations—those with variables separated, homogeneous equations, and linear equations—are precisely the equations for which an integrating factor is known.
2. The mathematical meaning of the word function has always been somewhat at variance with its meaning in ordinary language. A person's function consists of the work the person does. Apparently, Leibniz pictured the curve as a means for producing these lines, which were therefore functions of the curve.
3. The problem had been considered a generation earlier by Brook Taylor, who made the assumption that the restoring force on the string at any point and any time was proportional to the curvature of its shape at that point and time. Since the curvature is essentially the second derivative with respect to arc length, this condition, when linearized, amounts to the partial differential equation used by d'Alembert.
4. The treatise of Woodhouse is a textbook as much as a history, and its last chapter is a set of 29 examples posed as exercises for the reader with solutions provided. The book also marks an important transition in British mathematics. Woodhouse says in the preface that, “In a former Work, I adopted the foreign notation. . .”. The foreign notation was the Leibniz notation for differentials, in preference to the dot above the letter that Newton used to denote his fluxions. He says that he found this notation even more necessary in calculus of variations, since he would otherwise have had to adopt some new symbol for Lagrange's variation. But he then goes on to marvel that Lagrange had taken the reverse step of introducing Newton's fluxion notation into the calculus of variations.
5. As discussed in Chapter 27, the Muslim scholars ibn Sahl and al-Haytham knew that the ratio of the sines of the angles of incidence and refraction was constant at a point where two media meet. The Europeans Thomas Harriot, Willebrod Snell, and René Descartes derived the law of refraction from theoretical principles and deduced that the ratio of these sines is the ratio of the speeds of propagation in the two media. Fermat's principle, which was stated in a letter written in 1662, uses this law to show that the time of travel from a point in one medium to a point in the other is minimal.
6. Newton apparently recognized structural similarities between this problem and his own optimal-streamlining problem (see Goldstine, 1980, pp. 7–35).
7. A Latin proverb much in vogue at the time. It means literally “from [just] the claw [one can recognize] the Lion.”
8. This problem was Example 4 in Chapter 4 of the treatise.
9. One of his results is that a particle moving over a surface and free of any forces tangential to the surface will move along a geodesic of that surface. One cannot help seeing in this result an anticipation of the basic principle of general relativity (see Chapter 39 below).
10. This distinction was pointed out by Gauss as early as 1799, in his criticism of d’Alembert's 1746 proof of the fundamental theorem of algebra.
11. A brief definition of a harmonic function is that its graph is the surface of a nonvibrating flexible membrane.
12. As we saw in the last chapter, Berkeley flung these very words back at Newton.
13. This kind of reasoning was used by Abel in the nineteenth century to prove that there is no finite algebraic algorithm for solving the general equation of degree 5.
14. In her calculus textbook, Maria Gaetana Agnesi called this curve la versiera, meaning twisted. It was incorrectly translated into English, apparently because of the resemblance of this word to l'avversiera, meaning wife of the Devil.