The history of mathematics: A brief course (2013)
Part VII. Special Topics
Chapter 38. Projective and Algebraic Geometry and Topology
No area of modern mathematics is so difficult to summarize as geometry. Besides the projective and descriptive geometry developed during the Renaissance in connection with painting and engineering, the ancient problem of the parallel postulate resurfaced in the eighteenth century, leading to non-Euclidean geometry in the nineteenth. Descartes' analytic geometry infused the subject with algebra and, when algebra had mastered complex numbers, gave rise to the subject of algebraic geometry. Meanwhile, the application of calculus brought about the creation of differential geometry. The complicated curves and surfaces that could be handled by means of algebra and calculus led to further generalizations, and combinatorial, algebraic, and differential topology were the result. Finally, as an underpinning for all these subjects, the infusion of set theory into geometry brought about point-set topology in the twentieth century. We must employ drastic principles of selection to give even a hint of understanding of all this profound and beautiful mathematics. When we last looked at geometry, in Chapter 31, we discussed projective and descriptive geometry up to the mid-seventeenth century. In the present chapter, we shall discuss a small sampling of later developments in projective and algebraic geometry, along with various types of the more general geometry known as topology.
38.1 Projective Geometry
Projective geometry underwent a rapid development in the two centuries from 1650 to 1850. We shall discuss a sampling of the results and principles discovered.
38.1.1 Newton's Degree-Preserving Mapping
Newton described the mapping shown in Fig. 38.1 (Whiteside, 1967, Vol. VI, p. 269), in which the parallel lines BL and AO, the points A, B, and O are fixed from the outset, and the angle θ are specified in advance. These parameters determine the distances h and Δ and the angle ϕ. To map the figure GHI to its image ghi, first project each point G parallel to BL so as to meet the extension of AB at a point D. Next, draw the line OD meeting BL in point d. Finally, from d along the line making angle θ with BL, choose the image point g so that gd : Od : : GD : OD. The original point, according to Newton, had coordinates (BD, DG) and its image the coordinates (Bd, dg). If we let x = BD, y = DG, ξ = BD, and η = dg, the coordinate transformations in the two directions are
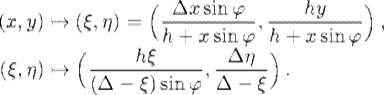
Newton noted that this kind of projection preserves the degree of an equation. Hence a conic section will remain a conic section, a cubic curve will remain a cubic curve, and so on, under such a mapping. In fact, if a polynomial equation p(x, y) = 0 is given whose highest-degree term is xmyn, then every term xpyq, when expressed in terms of ξ and η, will be a multiple of ξpηq/(Δ − ξ)p+q, so that if the entire equation is converted to the new coordinates and then multiplied by (Δ − ξ)m+n, this term will become ξpηq(Δ − ξ)m+n−p−q, which will be of degree m + n. Thus the degree of an equation does not change under Newton's mapping. These mappings are special cases of the transformations known as fractional-linear or Möbius transformations, after August Ferdinand Möbius (1790–1868), who developed them more fully. They play a vital role in algebraic geometry and complex analysis, being the only one-to-one analytic mappings of the extended complex plane onto itself. According to Coolidge (1940, p. 269), Edward Waring remarked in 1762 that fractional-linear transformations were the most general degree-preserving transformations.
Figure 38.1 Newton's degree-preserving projection.
38.1.2 Brianchon
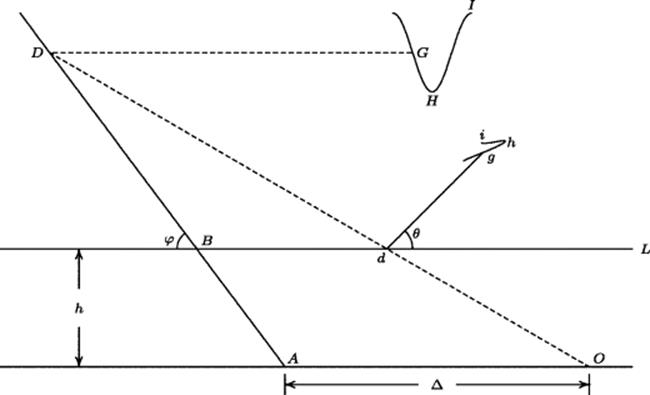
Pascal's work on the projective properties of conics was extended by Charles Julien Brianchon (1785–1864), who was also only a teenager when he proved what is now recognized as the dual of Pascal's theorem that the pairs of opposite sides of a hexagon inscribed in a conic meet in three collinear points. Pascal's theorem in the case of a circle is illustrated in Fig. 38.2. Brianchon's theorem asserts that the diagonals of a hexagon circumscribed about a conic are concurrent. The case of an ellipse is illustrated in Fig. 38.3.
Figure 38.2 Pascal's theorem for a circle.
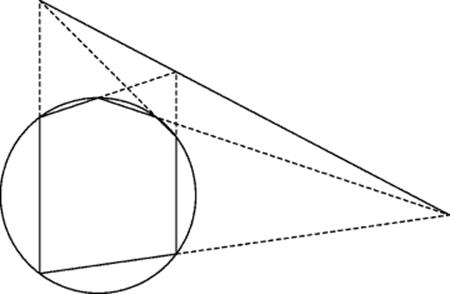
Figure 38.3 Brianchon's theorem for an ellipse.
38.1.3 Monge and his School
After a century of relative neglect, projective geometry revived at the Ecole Polytechnique under the students of Gaspard Monge (1746–1818), who was a master of the application of calculus to geometry. Felix Klein (1926, pp. 77–78) described his school as distinguished by “the liveliest spatial intuition combined in the most natural way possible with analytic operations.” Klein went on to say that Monge taught his students to make physical models, “not to make up for the deficiencies of their intuition but to develop an already clear and lively intuition.” As a military engineer, Monge had used his knowledge of geometry to design fortifications. His work in this area was highly esteemed by his superiors and declared a military secret. He wrote a book on descriptive geometry and one on the applications of analysis to geometry, whose influence appeared in the work of his students. Klein says of the second book that it “reads like a novel.” In this book, Monge analyzed quadric surfaces with extreme thoroughness.
Monge is regarded as the founder of descriptive geometry, which is based on the same principles of perspective as projective geometry but more concerned with the mechanics of representing three-dimensional objects properly in two dimensions and the principles of interpreting such representations. Monge himself described the subject as the science of giving a complete description in two dimensions of those three-dimensional objects that can be defined geometrically. As such, it continues to be taught today under other names, such as mechanical drawing; it is the most useful form of geometry for engineers.
Monge's greatest student (according to Klein) was Jean-Victor Poncelet (1788–1867). He participated as a military engineer in Napoleon's invasion of Russia in 1812, was wounded, and spent a year in a Russian prison, where he busied himself with what he had learned from Monge. Returning to France, he published his Treatise on the Projective Properties of Figures in 1822, the founding document of modern projective geometry. Its connection with the work of Desargues shows in the first chapter, where Poncelet says he will be using the word projective in the same sense as the word perspective. In Chapter 3 he introduces the idea that all points at infinity in a plane can be regarded as belonging to a single line at infinity.1 These concepts brought out fully the duality between points and lines in a plane and between points and planes in three-dimensional space, so that interchanging these words in a theorem of projective geometry results in another theorem. The theorems of Pascal and Brianchon, as mentioned, are dual to each other.
38.1.4 Steiner
The increasing algebraization of geometry was opposed by the Swiss mathematician Jacob Steiner (1796–1863), described by Klein (1926, pp. 126–127) as “the only example known to me. . .of the development of mathematical abilities after maturity.” Steiner had been a farmer up to the age of 17, when he entered the school of the Swiss educational reformer Johann Heinrich Pestalozzi (1746–1827), whose influence was widespread, extending through the philosopher/psychologist Johann Friedrich Herbart (1776–1841), a mathematically inclined philosopher whose attempts to quantify sense impressions was an early form of mathematical psychology,2 down to Riemann, as will be explained in the next section.
Steiner was a peculiar character in the history of mathematics, who when his own creativity was in decline, adopted the ideas of others as his own without acknowledgment (see Klein, 1926, p. 128). But in his best years, around 1830, he had the brilliant idea of building space using higher-dimensional objects such as lines and planes instead of points, recognizing that these objects were projectively invariant. He sought to restore the ancient Greek “synthetic” approach to geometry, the one we have called metric-free, that is, independent of numbers and the concept of length. To this end, in his 1832 work on geometric figures he considered a family of mappings of one plane on another that resembles Newton's projection. Klein (1926, p. 129) found nothing materially new in this work, but admired the systematization that it contained. The Steiner principle of successively building more and more intricate figures by allowing simpler ones to combine geometrically was novel and had its uses, but according to Klein, encompassed only one part of geometry.
38.1.5 Möbius
Projective geometry was enhanced through the barycentric calculus invented by Möbius and expounded in a long treatise in 1827. This work contained a number of very useful innovations. Möbius' use of barycentric coordinates to specify the location of a point anticipated vector methods by some 20 years and proved its value in many parts of geometry. He used his barycentric coordinates to classify plane figures in new ways. As he explained in Chapter 3 of the second section of his barycentric calculus (Baltzer, 1885, pp. 177–194), if the vertices of a triangle were specified as A, B, C, and one considered all the points that could be written as aA + bB + cC, with the lengths of the sides and the proportions of the coefficients a : b : c given, all such figures would be congruent (he used the phrase “equal and similar”). If one specified only the proportions of the sides instead of their lengths, all such figures would be similar. If one specified only the proportions of the coefficients, the figures would be in an affine relationship, a word still used to denote a linear transformation followed by a translation in a vector space. Finally, he introduced the relation of equality (in area).
The work of Möbius on the barycentric calculus was reviewed by a French author with the initials A.C. It has been thought that this was Cauchy,3 Grattan-Guinness says, however, that the reviewer was probably not Cauchy. The reviewer, as reported by Baltzer (1885, pp. xi–xii), was cautious at first, saying that the work was “a different method of analytic geometry whose foundation is certainly not so simple; only a deeper study can enable us to determine whether the advantages of this method will repay the difficulties.” After reporting on the new classification of figures in Part 2, he commented:
One must be very confident of taking a large step forward in science to burden it with so much new terminology and to demand that your readers follow you in investigations presented to them in such a strange manner.
Finally, after reporting some of the results from Part 3, he concluded that, “It seems that the author of the barycentric calculus is not familiar with the general theory of duality between the properties of systems of points and lines established by M. Gergonne.”4 This duality (gegenseitiges Entsprechen) was discussed in Chapters 4 and 5 of Part 3. This comment apparently alludes to ideas in Gergonne's papers that the reviewer found missing in the work of Möbius. Chapters 4 and 5 contain some of the most interesting results in the work. Chapter 4, for example, discusses conic sections and uses the barycentric calculus to prove that two distinct parabolas can be drawn through four coplanar points, provided none of them lies inside the triangle formed by the other three.
Möbius is best remembered for two concepts, the Möbius transformation, and the Möbius band. A Möbius transformation, by which we now understand a mapping of the complex plane into itself, ![]() , of the form
, of the form
![]()
can be found in his 1829 paper on metric relations in line geometry. He gave such transformations with real coefficients in terms of the two coordinates (x, y), the real and imaginary parts of what we now write as the complex number z, and showed that they were the most general one-to-one transformations that preserve collinearity. The Möbius band is discussed in Section 38.3 below.
38.2 Algebraic Geometry
Like Descartes, Newton made a classification of curves according to the degree of the equations that represent them or, rather, according to the maximal number of points in which they could intersect a straight line. As Descartes had argued for the use of any curves that could be generated by one parameter, excluding spirals and the quadratrix because they required two independent motions to be coordinated, Newton likewise argued that geometers should either confine themselves to conic sections or else allow any curve having a clear description. In his Universal Arithmetick, he mentioned in particular the trochoid,5 which makes it possible to divide an angle into any number of equal parts, as a useful curve that is simple to describe.
Descartes had begun the subject of algebraic geometry by classifying algebraic curves into “genera,” and, as just shown, Newton gave an alternative classification of curves, also based on algebra, although he included some curves that we would call transcendental, which could intersect a line in infinitely many points. The general study of algebraic curves p(x, y) = 0, where p(x, y) is a polynomial in two variables, began with Colin Maclaurin (1698–1746), who in his Geometria organica of 1720 remarked that a cubic curve was not uniquely determined by nine points, even though nine points apparently suffice to determine the coefficients of any polynomial p(x, y) of degree 3, up to proportionality and hence ought to determine a unique curve p(x, y) = 0. Two distinct cubic curves generally intersect in nine points, so that some sets of nine points do not determine the curve uniquely. This fact was later (1748) noted by Euler as well, and finally, by Gabriel Cramér (1704–1752), who also noted Maclaurin's priority in the discovery that a curve of degree m and a curve of degree n meet generally in mn points.
This curious fact is called Cramér's paradox after Cramér published it in a 1750 textbook on algebraic curves. Although he correctly explained why more than one curve of degree n can sometimes be made to pass through n(n + 3)/2 points—because the equations for determining the coefficients from the coordinates of the points might not be independent—he noted that in that case there were actually infinitely many such curves. That, he said, was a real paradox. Incidentally, it was in connection with the determination of the coefficients of an algebraic curve through given points that Cramér stated Cramér's rule for solving a system of linear equations by determinants.6
38.2.1 Plücker
A number of excellent German, Swiss, and Italian geometers arose in the nineteenth century. As an example, we take Julius Plücker (1801–1868), who was a professor at the University of Bonn for the last 30 years of his life. Plücker himself remembered (Coolidge, 1940, p. 144) that when young he had discovered a theorem in Euclidean geometry: The three lines containing the common chords of pairs of three intersecting circles are all concurrent. Plücker's proof of this theorem is simplicity itself. Suppose that the equations of the three circles are A = 0, B = 0, C = 0, where each equation contains x2 + y2 plus linear terms. By subtracting these equations in pairs, we get the quadratic terms to drop out, leaving the equations of the three lines containing the three common chords: A − B = 0, A − C = 0, B − C = 0. But it is manifest that any two of these equations imply the third, so that the point of intersection of any two also lies on the third line.
Plücker's student Felix Klein (1926, p. 122) described a more sophisticated specimen of this same kind of reasoning by Plücker to prove Pascal's theorem that the opposite sides of a hexagon inscribed in a conic, when extended, intersect in three collinear points. The proof goes as follows: The problem involves two sets, each containing three lines, six of whose nine pairwise intersections lie on a conic section. The conic section has an equation of the form q(x, y) = 0, where q(x, y) is quadratic in both x and y. Represent each line by a linear polynomial of the form ajx + bjy + cj, the jth line being the set of (x, y) where this polynomial equals zero, and assume that the lines are numbered in clockwise order around the hexagon. Form the polynomial
![]()
with the parameter μ to be chosen later. This polynomial vanishes at all nine intersections of the lines. Line 1, for example, meets lines 2 and 6 inside the conic and line 4 outside it.
Now, when y is eliminated from the equations q(x, y) = 0 and s(x, y) = 0, the result is an equation t(x) = 0, where t(x) is a polynomial of degree at most 6 in x. This polynomial must vanish at all of the simultaneous zeros of q(x, y) and s(x, y). We know that there are six such zeros for every μ. However, it is very easy to choose μ so that there will be a seventh common zero. With that choice of μ, the polynomial t(x) must have seven zeros, and hence must vanish identically. But since t(x) was the result of eliminating y between the two equations q(x, y) = 0 and s(x, y) = 0, it now follows that q(x, y) divides s(x, y). That is, the equation s(x, y) = 0 can be written as (ax + by + c)q(x, y) = 0. Hence its solution set consists of the conic and the line ax + by + c = 0, and this line must contain the other three points of intersection.
Conic sections and quadratic functions in general continued to be a source of new ideas for geometers during the early nineteenth century. Plücker liked to use homogeneous coordinates to give a symmetric description of a quadric surface (a surface whose equation is p(x, y, z) = 0, where p(x, y, z) is a polynomial of degree 2). To take the simplest example, consider the sphere of radius 2 in three-dimensional space with center at (2, 3, 1), whose equation is
![]()
If x, y, and z, are replaced by ξ/τ, η/τ, and ζ/τ and each term is multiplied by τ2, this equation becomes a homogeneous quadratic relation in the four variables (ξ, η, ζ, τ):
![]()
The sphere of unit radius centered at the origin then has the simple equation τ2 − ξ2 − η2 − ζ2 = 0. Plücker introduced homogeneous coordinates in 1830. One of their advantages is that if τ = 0, but the other three coordinates are not all zero, the point (ξ, η, ζ, τ) can be considered to be located on a sphere of infinite radius. The point (0, 0, 0, 0) is excluded, since it seems to correspond to all points at once.
Homogeneous coordinates correspond very well to the ideas of projective geometry, in which a point in a plane is identified with all the points in three-dimensional space that project to that point from a point outside the plane. If, for example, we take the center of projection as (0, 0, 0) and identify the plane with the plane z = 1, that is, each point (x, y) is identified with the point (x, y, 1), the points that project to (x, y) are all points (tx, ty, t), where t ≠ 0. Since the equation of a line in the (x, y)-plane has the form ax + by + c = 0, one can think of the coordinates (a, b, c) as the coordinates of the line. Here again, multiplication by a nonzero constant does not affect the equation, so that these coordinates can be identified with (ta, tb, tc) for any t ≠ 0. Notice that the condition for the point (x, y) to lie on the line (a, b, c) is that ![]() (a, b, c), (x, y, 1)
(a, b, c), (x, y, 1) ![]() = a · x + b · y + c · 1 = 0, and this condition is unaffected by multiplication by a constant. The duality between points and lines in a plane is then clear. Any triple of numbers, not all zero, can represent either a point or a line, and the incidence relation between a point and a line is symmetric in the two. We might as well say that the line lies on the point as that the point lies on the line.
= a · x + b · y + c · 1 = 0, and this condition is unaffected by multiplication by a constant. The duality between points and lines in a plane is then clear. Any triple of numbers, not all zero, can represent either a point or a line, and the incidence relation between a point and a line is symmetric in the two. We might as well say that the line lies on the point as that the point lies on the line.
Equations can be written in either line coordinates or point coordinates. For example, the equation of an ellipse can be written in homogeneous point coordinates (ξ, η, ζ) as
![]()
or in line coordinates (λ, μ, ν) as
![]()
where the geometric meaning of this last expression is that the line (λ, μ, ν) is tangent to the ellipse.
38.2.2 Cayley
Homogeneous coordinates provided important invariants and covariants7 in projective geometry. One such invariant under orthogonal transformations (those that leave the sphere fixed) is the dihedral angle between two planes Ax + By + Cz = D and A′ x + B′ y + C′ z = D′, given by
(38.1) ![]()
In his “Sixth memoir on quantics,” published in the Transactions of the London Philosophical Society in 1858, Cayley fixed a “quantic” (quadratic form) ∑αijuiuj, whose zero set was a quadric surface that he called the absolute, and defined angles by analogy with Eq. (38.1) and other metric concepts by a similar analogy. In this way he obtained the general projective metric, commonly called the Cayley metric. It allowed metric geometry to be included in projective geometry. As Cayley said, “Metrical geometry is thus a part of descriptive geometry and descriptive geometry is all geometry.” By suitable choices of the absolute, one could obtain the geometry of all kinds of quadric curves and surfaces, including the non-Euclidean geometries studied by Gauss, Lobachevskii, Bólyai, and Riemann, all of which will be discussed in Chapter 40. Klein (1926, p. 150) remarked that Cayley's models were the most convincing proof that these geometries were consistent.
38.3 Topology
Projections distort the shape of geometric objects, so that some metric properties are lost. Some properties, however, remain because the number of intersections of two lines does not change. The study of space focusing on such very general properties as connections and intersections has been known by various names over the centuries. Latin has two words, locus and situs, meaning roughly place and position. The word locus is one that we still use today to denote the path followed by a point moving subject to stated constraints, although, since the introduction of set theory, a locus is more often thought of statically as the set of points satisfying a given condition. It was the translation of the Greek word tópos used by Pappus for the same concept. Since locus was already in use, Leibniz fastened on situs and mentioned the need for a geometry or analysis of situs in a 1679 letter to Huygens.8 The meaning of geometria situs and analysis situs evolved gradually. It seems to have been Johann Benedict Listing (1808–1882) who, some time during the 1830s, realized that the Greek root was available. The word topology first appeared in the title of his 1848 book Vorstudien zur Topologie (Prolegomena to Topology). Like geometry itself, topology has bifurcated several times, so that one can now distinguish combinatorial, algebraic, differential, and point-set topology.
38.3.1 Combinatorial Topology
The earliest result that deals with the combinatorial properties of figures is now known as the Euler characteristic, although Descartes is entitled to some of the credit. In a work on polyhedra that he never published, Descartes defined the solid angle at a vertex of a closed polyhedron to be the difference between a complete revolution (4 right angles) and the sum of the angles at that vertex. He noted that the sum of the solid angles in any closed polyhedron was exactly eight right angles. Descartes' work was found among his effects after he died. By chance, Leibniz saw it a few decades later and made a copy of it. When it was found among Leibniz’ papers, it was finally published. In the eighteenth century, Euler discovered that the sum of the angles at the vertices of a closed polyhedron was 4V − 8 right angles, where V is the number of vertices. Euler noted the equivalent fact that the number of faces and vertices exceeded the number of edges by 2. That is the formula now generally called Euler's formula:
![]()
Somewhat peripheral to the general subject of topology was Euler's analysis of the famous problem of the seven bridges of Königsberg9 in 1736. In Euler's day there were two islands in the middle of the River Pregel, which flows through Köngisberg (now Kaliningrad, Russia). These islands were connected to each other by a bridge, and one of them was connected by two bridges to each shore, the other by one bridge to each shore. The problem was to go for a walk and cross each bridge exactly once, returning, if possible, to the starting point. In fact, as one can easily see, it is impossible even to cross each bridge exactly once without boating or swimming across the river. Returning to the starting point merely adds another condition to a condition that is already impossible to fulfill. Euler proved this fact by labeling the two shores and the two islands A, B, C, and D and representing a hypothetical stroll as a “word,” such as ABCBD, in which the bridges are “between” the letters. He showed that any such path as required would have to be represented by an 8-letter word containing three of the letters twice and the other letter three times, which is obviously impossible. This topic belongs to what is now called graph theory; it is an example of the problem of unicursal tracing.
38.3.2 Riemann
The study of analytic functions of a complex variable turned out to require some concepts from topology. These issues were touched on in Riemann's 1851 doctoral dissertation at Göttingen, “Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse” (“Foundations for a general theory of functions of a complex variable”). Although all analytic functions of a complex variable, both algebraic and transcendental, were encompassed in Riemann's ideas, he was particularly interested in algebraic functions—that is, functions ![]() that satisfy a nontrivial polynomial equation
that satisfy a nontrivial polynomial equation ![]() . Algebraic functions are essentially and unavoidably multivalued. To take the simplest example, where
. Algebraic functions are essentially and unavoidably multivalued. To take the simplest example, where ![]() , every complex number z = a + bi has two distinct complex square roots:
, every complex number z = a + bi has two distinct complex square roots:
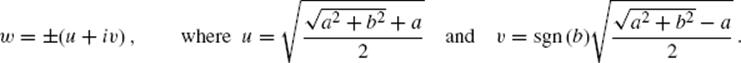
The square roots of the non-negative real numbers that occur here are assumed nonnegative. There is no way of choosing just one of the two values at each point that will result in a continuous function ![]() . In particular, it is easy to show that any such choice must have a discontinuity at some point of the circle |z| = 1.
. In particular, it is easy to show that any such choice must have a discontinuity at some point of the circle |z| = 1.
One way to handle this multivaluedness was to take two copies of the z-plane, labeled with subscripts as z1 and z2, and place one of the square roots in one plane and the other in the other. This technique was used by Cauchy and had been developed into a useful way of looking at complex functions by Victor Puiseux (1820–1883) in 1850. Indeed, Puiseux seems to have had the essential insight—preventing z from making a complete circuit around 0—that can be found in Riemann's work, although differently expressed. Riemann is known to have seen the work of Puiseux, although he did not cite it in his own work. He generally preferred to work out his own way of doing things and tended to ignore earlier work by other people. The difficulty with choosing one square root and sticking to it is that a single choice cannot be continuous on a closed path that encloses the origin but does not pass through it. Somewhere on such a path, there will be nearby points at which the function assumes two values that are close to being negatives of each other.
Riemann had the idea of cutting the two copies of the z-plane along a line running from zero to infinity (both being places where there is only one square root, assuming a bit about complex infinity). These two points are called branch points. Then if the lower edge of each plane is imagined as being glued to the upper edge of the other,10 the result is a single connected surface in which the origin belongs to both planes. On this new surface a continuous square-root function can be defined. It was the gluing that was really new here. Cauchy and Puiseux both had the idea of cutting the plane to keep a path from winding around a branch point and of using different copies of the plane to map different branches of the function.
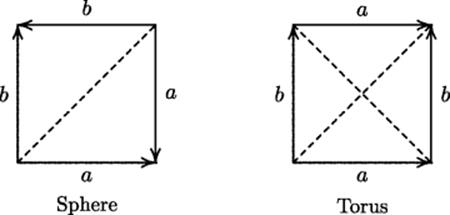
Riemann introduced the idea of a simply connected surface, one that is disconnected by any cut from one boundary point to another that passes through its interior without intersecting itself. He stated as a theorem that the result of such a cut would be two simply connected surfaces. In general, when a connected surface is cut by a succession of such crosscuts, as he called them, the number of crosscuts minus the number of connected components that they produce, plus 1, is a constant, called the order of connectivity of the surface. A sphere, for example, can be thought of as a square with adjacent edges glued together, as in Fig. 38.3. It is simply connected (has order of connectivity 0) because a diagonal cut divides it into two components. The torus, on the other hand, can be thought of as a square with opposite edges identified (see Fig. 38.4). To separate this surface into two components, it is necessary to cut the square at least twice, for example, either along both diagonals or through its center along two lines parallel to the sides. No single cut will do. The torus is thus doubly connected, with order of connectivity 1).
Figure 38.4 Left: The sphere, regarded as a square with edges identified, is disconnected by a diagonal cut. Right: Two cuts are required to disconnect the torus.
38.3.3 Möbius
One fact that had been thought well established about polyhedra was that in any polyhedron it was possible to direct the edges in such a way that one could trace around the boundary of each face by following the prescribed direction of its edges. Each face would be always to the left or always to the right as one followed the edges around it while looking at it from outside the polyhedron. This fact was referred to as the edge law (Gesetz der Kanten). The first discovery of a polyhedron that violated this condition11 was due to Möbius, sometime during the late 1850s. Möbius did not publish this work, although he did submit some of it to the Paris Academy as his entry to a prize competition in 1858. This work was edited and introduced by Curt Reinhardt (dates unknown) and published in Vol. 2 of Möbius' collected works. There in the first section, under the heading “one-sided polyhedra,” is a description of the Möbius band as we now know it (Fig. 38.5). After describing it, Möbius went on to say that although a triangulated polyhedron whose surface was two-sided will apparently contain only two-sided bands, nevertheless a triangulated one-sided polyhedron can contain both one-and two-sided bands.
Figure 38.5 Left: the projective plane triangulated and cut open. If two opposite edges with corresponding endpoints are glued together, the figure becomes a Möbius band. In three-dimensional space it is not possible to glue all the edges together as indicated. Right: the Möbius band as originally described by Möbius.
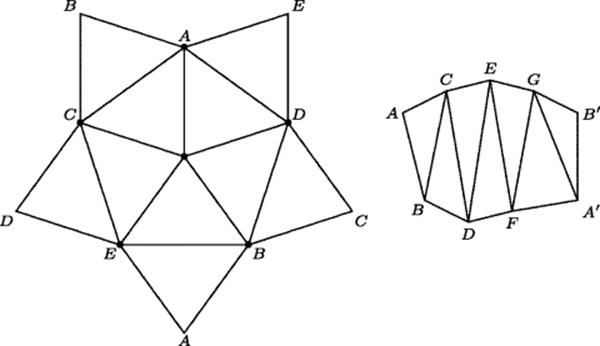
Möbius explored polyhedra and made a classification of them according to the number of boundary curves they possessed. He showed how more complicated polyhedra could be produced by gluing together a certain set of basic figures. He found an example of a triangulated polyhedron consisting of 10 triangles, six vertices, and 15 edges, rather than 14, as would be expected from Euler's formula for a closed polyhedron: V − E + F = 2. This figure is the projective plane, and cannot be embedded in three-dimensional space. If one of the triangular faces is removed, the resulting figure is the Möbius band, which can be embedded in three-dimensional space.
38.3.4 Poincaré's Analysis situs
Henri Poincaré (1854–1912) dealt with topological considerations frequently in his work in both complex function theory and differential equations. To set everything that he discovered down in good order, he wrote a treatise on topology called Analysis situs in 1895, published in the Journal de l'Ecole Polytechnique. This paper has been regarded as the founding document of modern algebraic topology.12 He introduced the notion of homologous curves—curves that (taken together) form the boundary of a surface. This notion could be formalized, so that one could consider formal linear combinations (now called chains) C = n1C1 + ![]() + nrCr of oriented curves Ci with integer coefficients ni. The interpretation of such a combination came from analysis: A line integral over C was interpreted as the number I = n1I1 +
+ nrCr of oriented curves Ci with integer coefficients ni. The interpretation of such a combination came from analysis: A line integral over C was interpreted as the number I = n1I1 + ![]() + nrIr, where Ij was the line integral over Cj. When generalized to k-dimensional manifolds (called variétés by Poincaré) and combined with the concept of the boundary of an oriented manifold as a cycle, this idea was the foundation of homology theory: The k-cycles (k-chains whose boundaries are the zero (k − 1)-chain—Poincaré called them closed varieties—form a group, of which the k-cycles that are the boundary of a (k + 1)-cycle form a subgroup. When two homologous cycles (cycles whose difference is a boundary) are identified, the resulting classes of cycles form the kth homology group. For example, in the sphere shown in Fig. 38.4, the diagonal that is drawn forms a cycle. This cycle is the complete boundary of the upper and lower triangles in the figure, and it turns out that any cycle on the sphere is a boundary. The first homology group of the sphere is therefore trivial (consists of only one element). For the torus depicted in Fig. 38.4, a and b are each cycles, but neither is a boundary, nor is any cycle ma + nb. On the other hand, the cycle formed by adding either diagonal to a + b is the boundary of the two triangles with these edges. Thus, the first homology group of the torus can be identified with the set of cycles ma + nb. Any other cycle will be homologous to one of these.
+ nrIr, where Ij was the line integral over Cj. When generalized to k-dimensional manifolds (called variétés by Poincaré) and combined with the concept of the boundary of an oriented manifold as a cycle, this idea was the foundation of homology theory: The k-cycles (k-chains whose boundaries are the zero (k − 1)-chain—Poincaré called them closed varieties—form a group, of which the k-cycles that are the boundary of a (k + 1)-cycle form a subgroup. When two homologous cycles (cycles whose difference is a boundary) are identified, the resulting classes of cycles form the kth homology group. For example, in the sphere shown in Fig. 38.4, the diagonal that is drawn forms a cycle. This cycle is the complete boundary of the upper and lower triangles in the figure, and it turns out that any cycle on the sphere is a boundary. The first homology group of the sphere is therefore trivial (consists of only one element). For the torus depicted in Fig. 38.4, a and b are each cycles, but neither is a boundary, nor is any cycle ma + nb. On the other hand, the cycle formed by adding either diagonal to a + b is the boundary of the two triangles with these edges. Thus, the first homology group of the torus can be identified with the set of cycles ma + nb. Any other cycle will be homologous to one of these.
Poincaré also introduced a second concept that has been of immense value in analyzing manifolds. He had been led to algebraic topology partly by his work in differential equations. In that connection, he imagined functions satisfying a set of differential equations and being permuted as a point moved around a closed loop. He was thus led to consider formal sums of loops starting and ending at a given point, two loops being equivalent if tracing them successively left the functions invariant. The resulting set of permutations was what he called the fundamental group or first homotopy group.13 He cautioned that, despite appearances, the first homotopy group was not the same thing as the first homology group, since there was no base point involved in the homology group. Moreover, he noted, while the order in which the cycles in a chain were traversed was irrelevant, the fundamental group was not necessarily commutative. He suggested redefining the term simply connected to mean having a trivial fundamental group. He gave examples to show that the homology groups do not determine the topological nature of a manifold, exhibiting three three-dimensional manifolds all having the same homology groups, but different fundamental groups and therefore not topologically the same (homeomorphic). He then asked a number of questions about fundamental groups, one of which has become famous. Given two manifolds of the same number of dimensions having the same homotopy groups, are they homeomorphic? Like Fermat's last theorem, this question has been attacked by many talented mathematicians. Many cases of it were settled, but not the important case of the sphere in three dimensions. For that case, many partial results were produced, and many proofs were proposed for a positive answer to the question, but until recently, all such proofs were found wanting. At last, in the first decade of the twentieth century, the Russian mathematician Grigorii Perelman (b. 1966) of the Steklov Institute in St. Petersburg gave a proof of the positive answer.14
38.3.5 Point-Set Topology
Topology is sometimes popularly defined as “rubber-sheet geometry,” in the sense that the concepts it introduces are invariant under moving and stretching, provided that no tearing takes place. In the kinds of combinatorial topology just discussed, those concepts usually involve numbers in some form or other—the number of independent cycles on a manifold, the Euler characteristic (the number V − E + F when a surface is partitioned), and so forth. But there are also topological concepts not directly related to number. One of these concepts, that of a Riemann surface, was designed for the needs of algebraic geometry and complex analysis. A quite different kind of topology, known as point-set topology, arose in complex and real analysis, but was mostly applied in real analysis, where it forms a large part of the subject matter.
The simplest and most intuitive of these concepts is that of connectedness or continuity. This word denotes a deep intuitive idea that was the source of many paradoxes in ancient times, such as the paradoxes of Zeno. In fact, it is impossible to prove the fundamental theorem of algebra without this concept.15 For analysts, it was crucial to know that if a continuous function was negative at one point on a line and positive at another, it must assume the value zero at some point between the two points (the intermediate-value property). That property eventually supplanted earlier definitions of continuity, and the property now taken as the definition of continuity is designed to make this proposition true. The clarification of the ideas surrounding continuity occurred in the early part of the nineteenth century, as mentioned in Chapter 34. Once serious analysis of this concept was undertaken, it became clear that many intuitive assumptions about the connectedness of curves and surfaces had been made from the beginning of deductive geometry. These continuity considerations complicated the theory of functions of a real variable for some decades until adequate explanations were found. A good example of such problems is provided by Dedekind's construction of the real numbers, which will be discussed in Chapter 42 and which he presented as a solution to the problem of defining what is meant by a continuum.
Problems and Questions
Mathematical Problems
38.1 How can Pascal's theorem for an ellipse be deduced from the special case of a circle? How do you interpret the situation when one pair of opposite sides is parallel?
38.2 Fill in the details of Plücker's proof of Pascal's theorem, as follows: Suppose that the equation of the conic is q(x, y) = y2 + r1(x)y + r2(x) = 0, where r1(x) is a linear polynomial and r2(x) is quadratic. Choose coordinate axes not parallel to any of the sides of the inscribed hexagon and such that the x-coordinates of all of the vertices of the hexagon will be different, and also choose the seventh point where t(x) = 0 to have x-coordinate different from those of the six vertices. Then suppose that the polynomial generated by the three lines is s(x, y) = y3 + t1(x)y2 + t2(x)y + t3(x) = 0, where tj(x) is of degree j, j = 1, 2, 3. Then there are polynomials uj(x) of degree j, j = 1, 2, 3, such that
![]()
We need to show that u2 ≡ 0 and u3 ≡ 0. At the seven points on the conic where both q(x, y) and s(x, y) vanish, it must also be true that u2(x)y + u3(x) = 0. Rewrite the equation q(x, y) = 0 at these seven points as
![]()
and observe that at these seven points u2y = − u3, so that the polynomial ![]() , which is of degree 6, has seven distinct zeros. It must therefore vanish identically, and that means that
, which is of degree 6, has seven distinct zeros. It must therefore vanish identically, and that means that
![]()
This means that either u2 is identically zero, which implies that u3 also vanishes identically, or else u2 divides u3. Prove that in the second case the conic must be a pair of lines, and give a separate argument in that case.
38.3 Consider the general cubic equation
![]()
which has 10 coefficients. Show that if this equation is to hold for the 10 points (1, 0), (2, 0), (3, 0), (4, 0), (0, 1), (0, 2), (0, 3), (1, 1), (2, 2), (1, − 1), all 10 coefficients A,. . ., J must be zero. In general, then, it is not possible to pass a curve of degree 3 through any 10 points in the plane. Use linear algebra to show that it is always possible to pass a curve of degree 3 through any nine points, and that the curve is generally unique.
On the other hand, two different curves of degree 3 generally intersect in 9 points, a result known as Bézout's theorem after Etienne Bézout (1730–1783), who stated it around 1758, although Maclaurin had stated it earlier. How does it happen that while nine points generally determine a unique cubic curve, two distinct cubic curves generally intersect in nine points? [Hint: Suppose that a set of eight points {(xj, yj) : j = 1,. . ., 8} is given for which the system of equations for A,. . ., J has rank 8. Although the system of linear equations for the coefficients is generally of rank 9 if another point is adjoined to this set, there generally is a point (x9, y9), namely the ninth point of intersection of two cubic curves through the other eight points, for which the rank will remain at 8.]
Historical Questions
38.4 What was the unique feature of Steiner's approach to geometry that made it an advance over previous work?
38.5 In what sense are the theorems of Pascal (Chapter 31) and Brianchon dual to each other?
38.6 In what way did Cayley's concept of the absolute unify geometry?
Questions for Reflection
38.7 Explain Cramér's paradox, and why it is not a contradiction.
38.8 Why are Möbius transformations useful in algebraic geometry and complex analysis?
38.9 What underlying harmony and unity is responsible for the fact that Pascal's theorem can be proved both projectively (from the case of a circle) and algebraically, as Plücker did it?
Notes
1. Field and Gray (1987, p. 185) point out that Kepler had introduced points at infinity in a 1604 work on conic sections, so that a parabola would have two foci.
2. Herbart's 1824 book Psychologie als Wissenschaft, neu gegründet auf Erfahrung, Metaphysik, und Mathematik (Psychology as Science on a New Foundation of Experiment, Metaphysics, and Mathematics) is full of mathematical formulas involving the strength of sense impressions, manipulated by the rules of algebra and calculus. Klein (1926, pp. 127–128) has nothing good to say about the more extreme recommendations of these men, calling their recommendations “pedagogical monstrosities.”
3. Cauchy was able to read German, not a common accomplishment for French mathematicians in the 1820s, when the vast majority of mathematical papers of significance were written in French.
4. Joseph Gergonne (1771–1859). Besides his work in geometry, he is best remembered as the founder (in 1810) of the journal Annales des mathématiques pures et appliquées.
5. A trochoid is the locus of a point rigidly attached to a rolling wheel. If the point lies between the rim and the center, the trochoid is called a curtate cycloid. If the point lies outside the rim, the trochoid is a prolate cycloid. If the point is on the rim, the trochoid is called simply a cycloid. The names come from the Greek words trokhós (wheel) and kýklos (circle).
6. As mentioned in Chapter 24, the solution of linear equations by determinants had been known to Seki K![]() wa and Leibniz. Thus, Cramér has two mathematical concepts named after him, and in both cases he was the third person to make the discovery.
wa and Leibniz. Thus, Cramér has two mathematical concepts named after him, and in both cases he was the third person to make the discovery.
7. According to Klein (1926, p. 148), the distinction between an invariant and a covariant is not essential. An algebraic expression that remains unchanged under a family of changes of coordinates is a covariant if it contains variables, and it is an invariant if it contains only constants.
8. This letter was published in the 1888 edition of Huygens' Œuvres complètes, Vol. 8, p. 216. From the context it appears that Leibniz was calling for some simple way of expressing position “as algebra expresses magnitude.” If so, perhaps we now have what he wanted, in the form of vector analysis.
9. This problem, because it is simple to state and has an elegant solution, is extremely popular in mathematics survey courses for nonmajors. However, its significance in the wider world of topology is quite small, so that it contributes to a generally distorted popular picture of what mathematicians have achieved.
10. This gluing is shown in more detail in Chapter 41.
11. In fact, a closed nonorientable polyhedron cannot be embedded in three-dimensional space, so that the edge law is actually true for closed polyhedra in three-dimensional space.
12. Poincaré followed this paper with a number of supplements over the next decade.
13. In informal terms, a homotopy is a continuous deformation of one curve into another.
14. For this achievement and a number of other brilliant papers, which Perelman chose to publish on the Word-Wide Web rather than in a refereed journal, he was showered with honors, including a number of professorships, a prize of one million dollars, and the Fields Medal, the most prestigious award in the mathematical profession. Perelman, however, has refused to accept any of these honors.
15. Even the second of the four proofs that Gauss gave, which is generally regarded as a purely algebraic proof, required the assumption that an equation of odd degree with real coefficients has a real solution—a fact that relies on connectedness.