The history of mathematics: A brief course (2013)

Part VII. Special Topics

Chapter 40. Non-Euclidean Geometry

There are two opposite points of view that one might adopt when assessing the value of Euclid's axiomatic approach to geometry. On the one hand, one could argue that it was precisely the attempt to spell out all assumptions explicitly that led to an explicit statement of the parallel postulate and hence subjected it to scrutiny. Thus, Euclidean geometry really generated non-Euclidean. That fact is underscored by the total absence of any speculation along those lines by mathematical cultures not descended from Euclid. On the other hand, it was the Hindu–Arabic algebra that immensely increased the power of geometry through analytic, projective, algebraic, and differential geometry. This algebraic approach laid out myriad examples of non-Euclidean geometries. All one had to do was look at them to see the possibility of denying the parallel postulate. From that point of view, Euclid's geometry is merely one specimen among many, all of roughly equal value for science, and “non-Euclidean” geometry is an unnecessary name for all the other surfaces and manifolds that don't happen to be Euclidean.

The hold that Euclid had over the intellectual imagination of the West was vast in its extent. For centuries, the axiomatic approach to all kinds of knowledge was regarded as an ideal in every area of intellectual endeavor. The philosopher Baruch Spinoza (1632–1677), for example, wrote a book entitled Ethica ordine geometrico demonstrata.¹ From the time of Descartes on, mathematicians had found the algebra inherited from the Hindus and Muslims and developed into a powerful symbolic method to be far superior, and they were the first to turn to other methods and let Euclid fall into neglect. Yet even after differential geometry was well established and a variety of exotic surfaces became amenable to study, a few mathematicians were still treading the old Euclidean paths and trying to prove the parallel postulate. In the nineteenth century, several of these people became the pioneers of non-Euclidean geometry, developed axiomatically, just like Euclidean. However, they took advantage of the metric point of view and developed the trigonometry of their non-Euclidean planes. It was this infusion of algebra into their reasoning that eventually brought about the acceptance of their work. At the same time, despite the repairs made to the Euclidean system by Hilbert, the presence of other geometries with equal claim to validity at long last settled not only the question of the provability of that postulate, but made the whole edifice of Euclidean methodology irrelevant to mathematical progress. The work of Euclid, Archimedes, and Apollonius was no less remarkable for this shift in point of view. It remains an imposing intellectual achievement, just as the great stone monuments that continue to fascinate the imagination of modern people remain as a testimony to the genius of the builders. But no architect nowadays looks to Egyptian building methods for ideas or holds them up as a model to be imitated. Euclid and his contemporaries have a permanent place in our culture. A liberal education that attempts to acquaint students with the greatest human achievements should not neglect them. But they also should not be presented as the sum total of mathematical achievement. Non-Euclidean geometry has traditionally meant geometry with the parallel postulate replaced by some other postulate. It really should be taken to mean geometry that is simply independent of, and draws on other sources in addition to, Euclid, that is to say, 99% of what is now called geometry.

The centuries of effort by Hellenistic and Islamic mathematicians to establish the parallel postulate as a fact of nature began to be repeated in early modern Europe, as mathematicians tried to replace the postulate with some other assumption that seemed more obvious. Then, around the year 1800, a change in attitude took place, as a few mathematicians began to explore non-Euclidean geometries as if they might have some meaning after all. Within a few decades the full light of day dawned on this topic, and by the late nineteenth century, models of the non-Euclidean geometries inside Euclidean and projective geometry removed all doubt as to their consistency. This history exhibits a sort of parallelism (no pun intended) with the history of the classical construction problems and with the problem of solving higher-degree equations in radicals, all of which were shown in the early nineteenth century to be impossible tasks. In all three cases, group theory eventually played a role in understanding the issues.

40.1 Saccheri

The Jesuit priest Giovanni Saccheri (1667–1733), a professor of mathematics at the University of Pavia, published in the last year of his life the treatise Euclides ab omni nævo vindicatus (Euclid Acquitted of Every Blemish), a good example of the creativity a very intelligent person will exhibit when trying to retain a strongly held belief. Some of his treatise duplicated what had already been done by the Islamic mathematicians, including the study of Thabit quadrilaterals, that is, quadrilaterals having a pair of equal opposite sides and equal base angles or having having three right angles. Saccheri deduced with strict rigor all the basic properties of Thabit quadrilaterals with right angles at the base (see Chapter 27).² He realized that the fundamental question involved the summit angles of these quadrilaterals—Saccheri quadrilaterals, as they are now called. Since these angles were equal, the only question was whether they were obtuse, right, or acute angles. He showed in Propositions 5 and 6 that if one such quadrilateral had obtuse summit angles, then all of them did likewise, and that if one had right angles, then all of them did likewise. It followed by elimination and without further proof (Proposition 7, which Saccheri proved anyway) that if one of them had acute angles, then all of them did likewise. Not being concerned to eliminate the possibility of the right angle, which he believed was the true one, he worked to eliminate the other two hypotheses.

He showed that the postulate as Euclid stated it is true under the hypothesis of the obtuse angle. That is, two lines cut by a transversal in such a way that the interior angles on one side are less than two right angles will meet on that side of the transversal. As we know, that is because they will meet on both sides of the transversal, assuming it makes sense to talk of opposite sides. Saccheri remarked that the intersection must occur at a finite distance. Saccheri would soon be reasoning about points at infinity as if something were known about them, even though he had no careful definition of them.

It is true, as many have pointed out, that his proof of this fact uses the exterior angle theorem (Proposition 16 of Book 1 of Euclid) and hence assumes that lines are infinite.³ But Euclid himself, as later edited, states explicitly that two lines cannot enclose an area, so that Saccheri can hardly be faulted for dealing with only one Euclidean postulate at a time. Since the parallel postulate implies that the summit and base of a Saccheri quadrilateral must meet on both sides of the quadrilateral under the hypothesis of the obtuse angle, even a severe critic should be inclined to give Saccheri a passing grade when he rejects this hypothesis.

Having disposed of the hypothesis of the obtuse angle, Saccheri then joined battle (his phrase) with the hypothesis of the acute angle. Here again, he proved some basic facts about what we now call hyperbolic geometry. Given any quadrilateral having right angles at the base and acute angles at the summit, it follows from continuity considerations that the length of a perpendicular dropped from the summit to the base must reach a minimum at some point, and at that point it must also be perpendicular to the summit. Saccheri analyzed this situation in detail, describing in the process some of the phenomena that must occur in what is now called hyperbolic geometry. In terms of Fig. 40.1a,⁴ he considered all the lines like AF through the point A such that angle BAF is acute. He wished to show that they all intersected the line BE.

Figure 40.1 (a) Lines like AC and AD through A that intersect BE and those like AF and AG that share a common perpendicular with BE are separated by a line (AL) that is asymptotic to BE. (b) The angle defect of AB′ C′ is more than twice the defect of ABC.

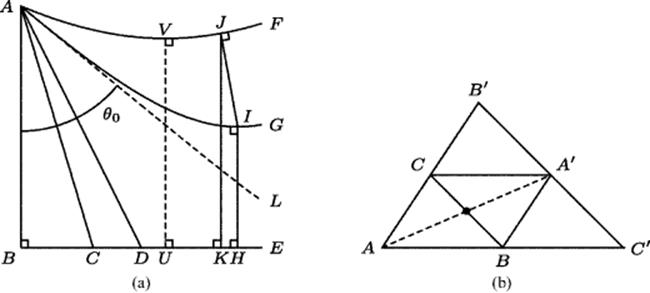
Saccheri proved that there must be at least one angle θ₀ for which the line AL making that angle neither intersects BE nor has a common perpendicular with it. This line, as Saccheri showed in Proposition 23, must approach BEasymptotically as we would say. At that point he made the small slip that had been warned against even in ancient times, assuming that “approaching” implies “meeting.” His intuition for hyperbolic geometry was very good, as he imagined a line UV perpendicular to BE moving away from AB to positions such as HI and the lines AV, AI, and so on from A perpendicular to the moving line rotating clockwise about A to make angles that decreased to θ₀. He then—too hastily, as we now know—drew the conclusion that θ₀ would have the properties of both of the sets of angles that it separated, that is, the line making this angle would intersect BE and would also have a common perpendicular with it. In fact, it has neither property. But Saccheri was determined to have both. As he described the situation, the hypothesis of the acute angle implied the existence of two straight lines that have a common perpendicular at the same point. In other words, there could be two distinct lines perpendicular to the same line at a point, which is indeed a contradiction. Unfortunately, the point involved was not a point of the plane, but is infinitely distant, as Saccheri himself realized. But he apparently believed that points and lines at infinity must obey the same axioms as those in the finite plane.

Once again, as in the case of Ptolemy, Thabit ibn-Qurra, and ibn al-Haytham, Saccheri had glimpsed a new, non-Euclidean kind of geometry, but resorted to procrustean methods to make it fit his Euclidean intuition.

40.2 Lambert and Legendre

The writings of the Swiss mathematician Johann Heinrich Lambert (1728–1777) seem modern in many ways. For example, he proved that π is irrational (specifically, that tan x and x cannot both be rational numbers), studied the problem of constructions with straightedge and a fixed compass, and introduced the hyperbolic functions and their identities as they are known today, including the notation sinh (x) and cosh (x). He wrote, but did not publish, a treatise on parallel lines, in which he pointed out that the hypothesis of the obtuse angle holds for great circles on a sphere and that the area of a spherical triangle is the excess of its angle sum over π times the square of the radius. He concluded that in a sphere of imaginary radius ir, whose area would be negative, the area of a triangle might be proportional to the excess of π over the angle sum. What a sphere of imaginary radius looks like took some time to discern, a full century, to be exact.

The hyperbolic functions that he studied turned out to be the key to trigonometry in this imaginary world. Just as on the sphere there is a natural unit of length (the radius of the sphere, for example), the same would be true, as Lambert realized, on his imaginary sphere. Such a unit could be selected in a number of ways. The angle of parallelism θ₀ mentioned above, for example, decreases steadily as the length AB increases. Every length is associated with an acute angle, and a natural unit of length might be the one whose angle of parallelism is half of a right angle. Or, it might be the length of the side of an equilateral triangle having a specified angle. In any case, Lambert at least recognized that he had not proved the parallel postulate. As he said, it was always possible to develop a proof of the postulate to the point that only some small, seemingly obvious point remained unproved, but that last point nearly always concealed an assumption equivalent to what was being proved.

Some of Lambert's reasoning was recast in more precise form by Legendre, who wrote a textbook of geometry used in many places during the nineteenth century, including (in English translation) the United States. Legendre, like Lambert and Saccheri, refuted the possibility that the angle sum of a triangle could be more than two right angles and attempted to show that it could not be less. Since the defect of a triangle—the difference between two right angles and its angle sum—is additive, in the sense that if a triangle is cut into two smaller triangles, the defect of the larger triangle is the sum of the defects of the two smaller ones, he saw correctly that if one could repeatedly double a triangle, eventually the angle sum would have to become negative, which was surely impossible. Unfortunately, the possibility of repeated doubling that he had in mind was just one of those small points mentioned by Lambert that turn out to be equivalent to the parallel postulate. In fact, it is rather easy to see that such is the case, since (Fig. 40.1b) asserting the possibility of drawing a line B′ C′ through a point A′ inside the angle CAB that intersects the extensions of both AB and AC is another way of saying that the line AB cannot be parallel to every line through A′ that intersects the extension of AC. (If it were, the limiting position of a line through A′ intersecting the extension of AC, as the point of intersection tends to infinity in the direction of C from A, would be a line parallel to both AB and AC, and there would thus be two lines through A parallel to this limiting line.)

40.3 Gauss

The parallel postulate was beginning to be understood by the end of the eighteenth century. Gauss, who read Lambert's work on parallels (which had been published posthumously), began to explore this subject as a teenager, although he kept his thoughts to himself except for letters to colleagues and never published anything on the subject. His work in this area was published in Vol. 8 of the later edition of his collected works. It was summarized by Klein (1926, pp. 58–59). In 1799, Gauss wrote to Farkas Bólyai (1775–1856), his classmate from Göttingen, that he could prove the parallel postulate provided that triangles of arbitrarily large area were admitted. Such a confident statement can only mean that he had developed the metric theory of hyperbolic geometry to a considerable extent. Five years later he wrote again to explain the error in a proof of the parallel postulate proposed by Bólyai. Gauss, like Lambert, realized that a non-Euclidean space would have a natural unit of length, and mentioned this fact in a letter of 1816 to his student Christian Ludwig Gerling (1788–1864), proposing as unit the side of an equilateral triangle whose angles were 59° 59′ 59.99999. . . ″.⁵ To Gauss' surprise, in 1818 he received from Gerling a paper written by Ferdinand Karl Schweikart (1780–1859), a lawyer then in Marburg, who had developed what he called astral geometry. It was actually hyperbolic geometry, and Schweikart had gone far into it, since he knew that there was an upper bound to the area of a triangle in this geometry, that its metric properties depended on an undetermined constant C (the distance, measured in units equal to the radius of curvature, at which the angle of parallelism is half of a right angle), and that it contained a natural unit of length, which he described picturesquely by saying that if that length were the radius of the earth, then the line joining two stars would be tangent to the earth. Gauss wrote back to correct some minor points of bad drafting on Schweikart's part (for example, Schweikart neglected to say that the stars were assumed infinitely distant), but generally praising the work. In fact, he communicated his formula for the limiting area of a triangle⁶:

By coincidence, Schweikart's nephew Franz Adolph Taurinus (1794–1874), also a lawyer, who surely must have known of his uncle's work in non-Euclidean geometry, sent Gauss his attempt at a proof of the parallel postulate in 1824. Gauss explained the true situation to Taurinus under strict orders to keep the matter secret. The following year, Taurinus published a treatise Geometriæ prima elementa (First Elements of Geometry) in which he accepted the possibility of other geometries. Gauss wrote to the astronomer–mathematician Friedrich Wilhelm Bessel (1784–1846) in 1829 that he had been thinking about the foundations of geometry off and on for nearly 40 years (in other words, from the age of 12 on), saying that his investigations were “very extensive,” but probably wouldn't be published, since he feared the controversy that would result. Some time during the mid-1820s, the time when he was writing and publishing his fundamental work on differential geometry, Gauss wrote a note—which, typically, he never published—in which he mentioned that revolving a tractrix about its asymptote produced a surface that is the opposite of a sphere. This surface turns out to be a perfect local model of the non-Euclidean geometry in which the angle sum of a triangle is less than two right angles. It is now called a pseudosphere. This same surface was discussed a decade later by Ferdinand Minding, who pointed out that some pairs of points on this surface can be joined by more than one minimal path, just like antipodal points on a sphere.

40.4 The First Treatises

By 1820, the consistency of non-Euclidean geometry was beginning to become plain. As more and more mathematicians worked over the problem and came to the same conclusion, from which others gained insight little by little, all that remained was a slight push to tip the balance from attempts to prove the parallel postulate to the acceptance of alternative hypotheses. The fact that this extra step was taken by several people nearly simultaneously can be expressed poetically, as it was by Felix Klein (1926, p. 57), who referred to “one of the remarkable laws of human history, namely that the times themselves seem to hold the great thoughts and problems and offer them to heads gifted with genius when they are ripe.” But we need not be quite so lyrical about a phenomenon that is entirely to be expected: When many intelligent people who have received similar educations work on a problem, it is not surprising when more than one of them makes the same discovery.

The credit for first putting forward hyperbolic geometry for serious consideration must belong to Schweikart, since Gauss was too reticent to do so. However, credit for the first full development of it, including its trigonometry, is due to the Russian mathematician Nikolai Ivanovich Lobachevskii (1792–1856) and the Hungarian János Bólyai (1802–1860), son of Farkas Bólyai. Their approaches to the subject are very similar. Both developed the geometry of the hyperbolic plane and then extended it to three-dimensional space. In three-dimensional space they considered the entire set of directed lines parallel to a given directed line in a given direction. Then they showed that a surface (now called a horosphere) that cuts all of these lines at right angles has all the properties of a Euclidean plane. By studying sections of this surface they were able to deduce the trigonometry of their new geometry. The triangle formulas fully justify Lambert's assertion that this kind of geometry is that of a sphere of imaginary radius. Here, for example, is the Pythagorean theorem for a right triangle of sides a, b, c in spherical and hyperbolic geometry, derived by both Lobachevskii and Bólyai, but not in the notation of hyperbolic functions. Since cos (ix) = cosh (x) the hyperbolic formula can be obtained from the spherical formula by replacing the radius r with ir, just as Lambert stated.

40.5 Lobachevskii's Geometry

Lobachevskii connected the parts of a hyperbolic triangle through his formula for the angle of parallelism, which is the angle θ₀ referred to above, as a function of the length AB. He gave this formula as

where α denotes the length AB and F(α) the angle θ₀. Here e could be any positive number, since the radius of curvature of the hyperbolic plane could not be determined. However, Lobachevskii found it convenient to take this constant to be e = 2.71828. . .. In effect, he took the radius of curvature of the plane as the unit of length. Lobachevskii gave the Pythagorean theorem, for example, as

Of the two nearly simultaneous creators of hyperbolic geometry and trigonometry, Lobachevskii was the first to publish, unfortunately in a journal of limited circulation. He was a professor at the provincial University of Kazan’ in Russia and published his work in 1826 in the proceedings of the Kazan’ Physico-Mathematical Society. He reiterated this idea over the next ten years or so, developing its implications. Like Gauss, he drew the conclusion that only observation could determine if actual space was Euclidean or not. As it happened, astronomers were just beginning to attempt measurements on the interstellar scale. By measuring the angles formed by the lines of sight from the earth to a given fixed star at intervals of six months, one could get the base angles of a gigantic triangle and thereby (since the angle sum could not be larger than two right angles, as everyone agreed) place an upper bound on the size of the parallax of the star (the angle subtended by the earth's orbit from that star). Many encyclopedias claim that the first measurement of stellar parallax was carried out in Königsberg by Gauss' correspondent Bessel in 1838 and that he determined the parallax of 61 Cygni to be 0.3 seconds. Russian historians credit another Friedrich Wilhelm, namely Friedrich Wilhelm Struve (1793–1864), who emigrated to Russia and is known there as Vasilii Yakovlevich Struve. He founded the Pulkovo Observatory in 1839. Struve determined the parallax of the star Vega in 1837. Attempts to determine stellar parallax must have been made earlier, since Lobachevskii cited such measurements in an 1829 work and claimed that the measured parallax was less than 0.000372″, which is much smaller than any observational error.⁷ As he said (see his collected works, Vol. 1, p. 207, quoted by S. N. Kiro, 1967, Vol. 2, p. 159):

At the very least, astronomical observations prove that all the lines amenable to our measurements, even the distances between celestial bodies, are so small in comparison with the length taken as a unit in our theory that the equations of (Euclidean) plane trigonometry, which have been used up to now must be true without any sensible error.

Thus, the acceptance of the consistency of hyperbolic geometry was accompanied by the rejection of any practical application of it in astronomy or physics. That situation was to change in the early twentieth century, with the advent of relativity.

Lobachevskii was unaware of the work of Gauss, since Gauss kept it to himself and urged others to do likewise. Had Gauss been more talkative, Lobachevskii would easily have found out about his work, since his teacher Johann Martin Christian Bartels (1769–1836) had been many years earlier a teacher of the 8-year-old Gauss and had remained a friend of Gauss. As it was, however, although Lobachevskii continued to perfect his “imaginary geometry,” as he called it, and wrote other mathematical papers, he made his career in administration, as rector of the University of Kazan'. He at least won some recognition for his achievement during his lifetime, and his writings were translated into French and German after his death.

Even though his imaginary geometry was not used directly to describe the world, Lobachevskii found some uses for it in providing geometric interpretations of formulas in analysis. In particular, his paper “Application of imaginary geometry to certain integrals,” which he published in 1836, was translated into German in 1904, with its misprints corrected (Liebmann, 1904). Just as we can compute the seemingly complicated integral

immediately by recognizing that it represents the area of a quadrant of a circle of radius r, he could use the differential form for the element of area in rectangular coordinates in the hyperbolic plane given by dS = (1/sin y′) dx dy, where y′ is the angle of parallelism for the distance y (in our terms sin y′ = sech y) to express certain integrals as the non-Euclidean areas of simple figures. In polar coordinates the corresponding element of area is dS = cot r′ dr dθ = sinh r dr dθ. Lobachevskii also gave the elements of volume in rectangular and spherical coordinates and computed 49 integrals representing hyperbolic areas and volumes, including the volumes of pyramids. Using the trigonometry of hyperbolic space, Lobachevskii evaluated a number of integrals, showing, for example, that

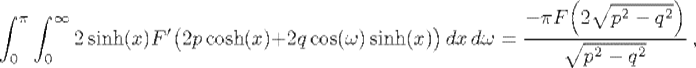
where F(x) is any continuously differentiable function on [0, ∞) such that lim _x→∞F(x) = 0 and p² > q² (Liebmann, 1904, p. 21).

40.6 János Bólyai

János Bólyai's career turned out less pleasantly than Lobachevskii's. Even though he had the formula for the angle of parallelism in 1823, a time when Lobachevskii was still hoping to vindicate the parallel postulate, he did not publish it until 1831, five years after Lobachevskii's first publication. Even then, he had only the limited space of an appendix to his father's textbook to explain himself. His father sent the appendix to Gauss for comments, and for once Gauss became quite loquacious, explaining that he had had the same ideas many years earlier, and that none of these discoveries were new to him. He praised the genius of the young Bólyai for discovering it, nevertheless. Bólyai the younger was not overjoyed at this response. He suspected Gauss of trying to steal his ideas. According to Paul Stäckel (1862–1919), who wrote the story of the Bólyais, father and son (quoted in Coolidge, 1940, p. 73), when Lobachevskii's work began to be known, Bólyai thought that Gauss was stealing his work and publishing it under the pseudonym Lobachevskii, since “it is hardly likely that two or even three people knowing nothing of one another would produce almost the same result by different routes.”

40.7 The Reception of Non-Euclidean Geometry

Some time was required for the new world revealed by Lobachevskii and Bólyai to attract the interest of the mathematical community. Because it seemed possible—even easy—to prove that parallel lines exist or, equivalently, that the sum of the angles of a triangle could not be more than two right angles, one can easily understand why a sense of symmetry would lead to a certain stubbornness in attempts to refute the opposite hypothesis as well. Although Gauss had shown the way to a more general understanding with the concept of curvature of a surface (which could be either negative or positive) in the 1825 paper on differential geometry that was published in 1827, it took Riemann's inaugural lecture in 1854 (published in 1867), which made the crucial distinction between the unbounded and the infinite, to give the proper perspective. As Gray (2005, p. 514) says

[N]ot only was Riemann hostile to the axiomatic treatment of geometry, he was also willing to believe that space was not infinite in extent either.

In 1868, the year after the publication of Riemann's lecture, Beltrami realized that Lobachevskii's theorems provide a model of the Lobachevskii–Bólyai plane in a Euclidean disk. This model is described by Gray (1989, p. 112), as follows. Imagine a directed line perpendicular to the Lobachevskii–Bólyai plane in Lobachevskii–Bólyai three-dimensional space. The entire set of directed lines that are parallel (asymptotic) to this line on the same side of the plane generates a unique horosphere tangent to the plane at its point of intersection with the line. Some of the lines parallel to the given perpendicular in the given direction intersect the original plane, and others do not. Those that do intersect it pass through the portion of the horosphere denoted Ω in Fig. 40.2. Shortest paths on the horosphere are obtained as its intersections with planes passing through the point at infinity that serves as its “center.” These paths are called horocycles. But there is only one horocycle through a given point in Ω that does not intersect a given horocycle, so that the geometry of Ω is Euclidean. As a result, we have a faithful mapping of the Lobachevskii–Bólyai plane onto the interior of a disk Ω in a Euclidean plane, under which lines in the plane correspond to chords on the disk. This model provides an excellent picture of points at infinity: They correspond to the boundary of the disk Ω. Lines in the plane are parallel if and only if the chords corresponding to them have a common endpoint. Lines that have a common perpendicular in the Lobachevskii–Bólyai plane correspond to chords whose extensions meet outside the circle. It is somewhat complicated to compute the length of a line segment in the Lobachevskii–Bólyai plane from the length of its corresponding chordal segment in Ω or vice versa, and the angle between two intersecting chords is not simply related to the angle between the lines they correspond to.⁸ Nevertheless these computations can be carried out from the trigonometric rules given by Lobachevskii. The result is a perfect model of the Lobachevskii–Bólyai plane within the Euclidean plane, obtained by formally reinterpreting the words line, plane, and angle. If there were any contradiction in the new geometry, there would be a corresponding contradiction in Euclidean geometry itself.

A variant of this model was later provided by Poincaré, who showed that the diameters and the circular arcs in a disk that meet the boundary in a right angle can be interpreted as lines, and in that case angles can be measured in the ordinary way. Distances are measured using the cross-ratio.

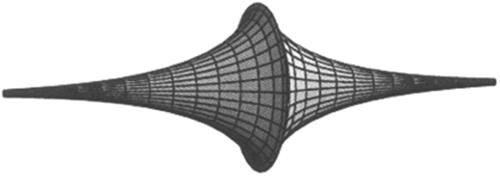
Beltrami also provided a model of a portion of the Lobachevskii–Bólyai plane that could be embedded in three-dimensional Euclidean space: the pseudosphere obtained by revolving a tractrix about its asymptote, as shown in Fig. 40.3.

The pseudosphere is not a model of the entire Lobachevskii–Bólyai plane, since its curvature has a very prominent discontinuity. The problem of finding a surface in three-dimensional Euclidean space that was a perfect model for the Lobachevskii–Bólyai plane, in the sense that its geodesics corresponded to straight lines and lengths and angles were measured in the ordinary way, remained open until Hilbert, in an article “Über Flächen von konstanter Gaußscher Krümmung” (“On surfaces of constant Gaussian curvature”), published in the Transactions of the American Mathematical Society in 1901, showed that no such surface exists.

In 1871, Felix Klein gave a discussion of the three kinds of plane geometry in his article “Über die sogennante nicht-Euklidische Geometrie” (“On the so-called non-Euclidean geometry”), published in the Mathematische Annalen. In that article, he gave the classification of them that now stands, saying that the points at infinity on a line were distinct in hyperbolic geometry, imaginary in spherical geometry, and coincident in parabolic (Euclidean) geometry.

Figure 40.2 Projection of the Lobachevskii–Bolyai plane onto the interior of a Euclidean disk.

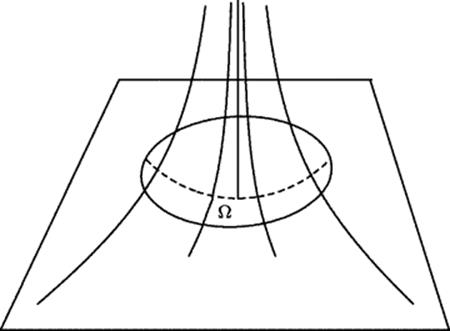
Figure 40.3 The pseudosphere. Observe that it has no definable curvature at its cusp. Elsewhere its curvature is constant and negative.

40.8 Foundations of Geometry

The problem of the parallel postulate was only one feature of a general effort on the part of mathematicians to improve on the rigor of their predecessors. This problem was particularly acute in the calculus, and the parts of calculus that raised the most doubts were those that were geometric in nature. Euclid, it began to be realized, had taken for granted not only the infinitude of the plane, but also its continuity, and in many cases, had not specified what ordering of points was needed on a line for a particular theorem to be true. If one attempts to prove these theorems without drawing any figures, it becomes obvious what is being assumed. It seemed obvious, for example, that a line joining a point inside a circle to a point outside the circle must intersect the circle in a point, but that fact could not be deduced from Euclid's axioms. A complete reworking of Euclid was the result, expounded in detail in Hilbert's Grundlagen der Geometrie (Foundations of Geometry), published in 1903. This book went through many editions and has been translated into English (Bernays, 1971). In Hilbert's exposition, the axioms of geometry are divided into axioms of incidence, order, congruence, parallelism, and continuity, and examples are given to show what cannot be proved when some of the axioms are omitted.

One thing is clear: No new comprehensive geometries are to be expected by pursuing the axiomatic approach of Hilbert. In a way, the geometry of Lobachevskii and Bólyai was a throwback even in its own time. The development of projective and differential geometry would have provided—indeed, did provide—non-Euclidean geometry by a natural expansion of the study of surfaces. It was Riemann, not Lobachevskii and Bólyai, who showed the future of geometry. Earlier, we quoted Gray (2005) on Riemann's hostility to the axiomatic Euclidean approach to geometry, often called synthetic geometry to distinguish it from analytic geometry, which presumes a metric and the use of numbers to express lengths and areas. Gray also noted (p. 513) that earlier investigators had followed an approach similar to Euclid's, accepting all his axioms except the parallel postulate and then trying to deduce the parallel postulate from the others, an approach that Riemann criticized in his inaugural lecture.

The real “action” in geometry since the early nineteenth century has been in differential, algebraic, and projective geometry. That is not to say that no new theorems can be produced in Euclidean geometry, only that their scope is very limited. There are certainly many such theorems. Coolidge, who undertook the herculean task of writing his History of Geometric Methods in 1940, stated in his preface that the subject was too vast to be covered in a single treatise and that “the only way to make any progress is by a rigorous system of exclusion.” In his third chapter, on “later elementary geometry,” he wrote that “the temptation to run away from the difficulty by not considering elementary geometry after the Greek period at all is almost irresistible.” But to attempt to build an entire theory, as Apollonius did, on the synthetic methods and limited techniques in the Euclidean tool kit, would be futile. Even Lobachevskii and Bólyai at least used analytic geometry and trigonometry to produce their results.

Problems and Questions

Mathematical Problems

40.1 Find the Gaussian curvature of the pseudosphere (see Chapter 39 for the definition of Gaussian curvature) obtained by revolving a tractrix about the x-axis. Its parameterization can be taken as

(The parameter u ranges over all real numbers, over an interval of length 2π.) Explain why the pseudosphere can be thought of as “a sphere of imaginary radius.”

40.2 Consider the two Pythagorean theorems in elliptic and hyperbolic geometry exhibited above, and assume the radius of curvature r is 1 in both cases. How long is the hypotenuse of an isosceles right triangle whose legs are each of length 3/2? Compare those lengths with the Euclidean length. Which of the three is smallest, and which largest?

40.3 Suppose two chords on a circle, say AB and CD are such that the tangents to the circle at A and B meet at a point on the extension of CD. (This means, in the Beltrami model of hyperbolic geometry, that AB is perpendicular to CD.) Prove that the tangents to the circle at C and D meet at a point on the extension of AB. In other words, if AB is perpendicular to CD, then CD is perpendicular to AB.

Historical Questions

40.4 In what ways did Saccheri duplicate unknowingly earlier work by Thabit ibn-Qurra. (See Chapter 27.)

40.5 Why did Gauss not publish his research in hyperbolic geometry?

40.6 What considerations finally led to the recognition by all practicing mathematicians that non-Euclidean geometry was consistent?

Questions for Reflection

40.7 Gauss realized that the geometry of physical space could be determined by observation, measuring the angle sum of very large triangles. (Theory shows that if space is homogeneous and non-Euclidean, then the larger a triangle is, the more its angle sum will differ from two right angles.) While he was involved in the survey of Hannover, he tried to determine the angles of a large triangle formed by three mountaintops. The three that he used, however, were not far enough apart to show any significant deviation from two right angles. If we use a radius or diameter of the earth's orbit as one side of the triangle and a nearby fixed star as the opposite vertex, the result is a truly large triangle. Such measurements became feasible during the early nineteenth century, and the two angles that can be measured from the earth (at opposite ends of the radius or diameter turned out to be very nearly, but not quite, two right angles. What is the proper conclusion? (1) Space is Euclidean, and the angle at the star (its parallax) is the supplement of the sum of these two angles? (2) Space is hyperbolic, and the angle at the star is smaller than that supplement? (3) Space is elliptic, and the angle at the star is larger than that supplement? Can these alternatives be distinguished by any observation from the earth?

40.8 Consistency and applicability are two very different issues in the world of mathematics. Granted that the consistency of non-Euclidean geometry was accepted by all mathematicians by the end of the nineteenth century, what applications have been found for these new geometries?

40.9 A rear-guard battle against enlightenment can be maintained for a surprisingly long time, even by people who have some scientific competence and even after there is a general consensus as to the truth. The long history of circle squarers and angle trisectors is a good example of this phenomenon. Most of those who work on such problems are non-mathematicians who simply don't understand the meaning of infinite precision. They waste their time, but can be made to recognize that a particular effort has failed, even as they turn again with renewed vigor to engage in this hopeless enterprise. Only a few of them are so logic-impaired that they are completely incapable of coherent reasoning. In the case of non-Euclidean geometry, this mathematical aberration sometimes expresses itself in attempts to prove the parallel postulate. One such attempt, from 80 years ago, was made by a quite intelligent and mathematically semi-literate scholar, the Rev. Dr. Jeremiah J. Callahan, president (at the time) of Duquesne University. Dr. Callahan wrote a treatise entitled Euclid or Einstein, in which he “proved” the parallel postulate by redefining parallel lines as “lines that are equidistant at equidistant points,” not realizing that the assumption that such lines exist is equivalent to the parallel postulate. He thought he had a proof that his definition was equivalent to Euclid's definition. One can have some sympathy for him on this point, since Euclid's definition of a line is “that which lies evenly along itself,” hardly a happy effort, since it would apply equally well to a circle.⁹

These “mathematical cranks” very frequently attempt to publish their work in newspapers or get them reported as news. What should mathematicians do when confronted by reporters asking them to comment on such work? Which is the better strategy: patient explanation or open contempt? Should the goal be to bring the crank to recognize his (it's almost always his, not her) errors? Or should it be to make the public laugh at the crank? Or to get the public to understand the proper relation between science and the nonspecialist citizen?

Notes

1. Ethics Demonstrated in Geometric Order. It was published a few months after Spinoza's death.

2. It is unlikely that Saccheri knew of the earlier work by Thabit ibn-Qurra and others. Although Arabic manuscripts stimulated a revival of mathematics in Europe, not all of them became known immediately. Some of those who did were neglected by historians of the subject. Coolidge (1940) gave the history of the parallel postulate, jumping directly from Proclus and Ptolemy to Saccheri, never mentioning any of the Muslim mathematicians.

3. Actually, the use of that proposition is confined to elaborations by the modern reader. The proof stated by Saccheri uses only the fact that lines are unbounded, that is, can be extended to any length. It is not necessary to require that the extension never overlap the portion already present.

4. Since the flat page is not measurably non-Euclidean, and wouldn't be even if spread out to cover the entire solar system, the kinds of lines that occur in hyperbolic geometry cannot be drawn accurately on paper. Our convention is the usual one: When asymptotic properties are not involved, draw the lines straight. When asymptotic properties need to be shown, draw them as hyperbolas. Actually, if the radius of curvature of the plane were comparable to the width of the page, two lines with a common perpendicular would diverge from each other like the graphs of cosh x and − cosh x, very rapidly indeed.

5. In comparison with the radius of curvature of space, this would be an extremely small unit of length. If space is curved negatively at all, however, its radius of curvature is so enormous that this unit would be very large.

6. The coefficient of π in this expression represents a unit area and is numerically equal to the square of the radius of curvature of the hyperbolic plane. However, there are no squares in hyperbolic geometry. An equiangular rhombus has acute angles at all four corners.

7. The vast distances between stars make terrestrial units of length inadequate. The light-year (about 9.5 · 10¹² km) is the most familiar unit now used, particularly good, since it tells us “what time it was” when the star emitted the light we are now seeing. Stellar parallax provides another unit, the parsec, which is the distance at which the radius of the earth's orbit subtends an angle of 1”. A parsec is about 3.258 light-years.

8. It can be shown that two mutually perpendicular lines correspond to chords having the property that the extension of each passes through the point of intersection of the tangents at the endpoints of the other. But it is far from obvious that this property is symmetric in the two chords, as perpendicularity is for lines.

9. The Greek word for a straight line is eutheîa, from eu- (good, well) and the root the- (put, set, as in our loan word thesis).