The history of mathematics: A brief course (2013)

Part VII. Special Topics

Chapter 44. Set Theory

Set theory is the common language now used in all areas of mathematics. Because it is the language everyone writes in, it is difficult to imagine a time when mathematicians did not use the word set or think of sets of points. Yet that time is not long past; it was less than 150 years ago. Before that time, mathematicians spoke of geometric figures, or they spoke of points and numbers having certain properties, without thinking of those points and numbers as being assembled in a set.

44.1 Technical Background

Although the founder of set theory, Georg Cantor (1845–1918), was motivated by both geometry and analysis, for reasons of space we shall discuss only the analytic connection, which was the more immediate one. It is necessary to introduce some technical details in order to explain how a problem in analysis leads to the general notion of a set and an ordinal number. We begin with the topic that Riemann developed for his 1854 lecture but did not use because Gauss preferred his geometric lecture. That topic was uniqueness of trigonometric series, and it was published in 1867, the year after Riemann's death. Riemann aimed at proving that if a trigonometric series converged to zero at every point, all of its coefficients were zero. That is,

Riemann assumed that the coefficients a_n and b_n tend to zero, saying that it was clear to him that without that assumption, the series could converge only at isolated points.¹ In order to prove his uniqueness theorem, Riemann integrated twice to form the continuous function

His object was to show that F(x) must be a linear function, so that would be a quadratic polynomial that was also periodic, and hence itself a constant, from which it would follow, first that a₀ = 0 = A, and then that all the other a_n and all the b_n are zero. To that end, he showed that its generalized second derivative

was zero wherever the original series converged to zero.² Riemann proved that in any case

The important implication of this last result is that the function F(x) cannot have a corner. If it has a right-hand derivative at a point, it also has a left-hand derivative at the point, and the two one-sided derivatives are equal. This fact was a key step in Cantor's work.

44.2 Cantor's Work on Trigonometric Series

In 1872, Cantor published his first paper on uniqueness of trigonometric series, finishing the proof that Riemann had set out to give: that a trigonometric series that converges to zero at every point must have all its coefficients equal to zero. In following the program of proving that F(x) is linear and hence constant, he observed that it was not necessary to assume that the series converged to zero at every point. A finite number of exceptions could be allowed, at which the series either diverged or converged to a nonzero value. For F(x) is certainly continuous, and if it is linear on [a, b] and also on [b, c], the fact that it has no corners implies that it must be linear on [a, c]. Hence any isolated exceptional point b could be discounted.

The question therefore naturally arose: Can one allow an infinite number of exceptional points? Here one comes up against a theorem known as the Bolzano–Weierstrass theorem, which asserts that the exceptional points cannot all be isolated. They must have at least one point of accumulation.³ But exceptional points isolated from other exceptional points could be discounted, just as before. That left only their points of accumulation. If these were isolated—in particular, if there were only finitely many of them—the no-corners principle would once again imply uniqueness of the series.

44.2.1 Ordinal Numbers

Cantor saw the obvious induction. Denoting the set of points of accumulation of a set P (what we now call the derived set) by P′, he knew that P′⊇ P ” ⊇ P ”′ ⊇ . Thus, if at some finite term in this non-increasing sequence of sets a finite set was obtained, the uniqueness theorem would remain valid. But the study of these sets of points of accumulation turned out to be even more interesting than trigonometric series themselves. No longer dealing with geometrically regular sets, Cantor was delving into point-set topology, as we now call it. No properties of a geometric nature were posited for the exceptional points he was considering, beyond the assumption that the sequence of derived sets contains a finite set as one of its terms (and all subsequent sets in the sequence will be empty). Although the points of any particular set might be easily describable, Cantor needed to discuss the general case. He needed the abstract concept of “set-hood.” Cantor felt compelled to dig to the bottom of this matter and soon abandoned trigonometric series to write a series of papers on “infinite linear point-manifolds.”⁴

Cantor noticed the possibility of defining the derived sets of transfinite order. If the nth-level derived set is P⁽ⁿ⁾, the nesting of these sets allows the natural definition of the derived set of infinite order P^(∞) as the intersection of all sets of finite order. But then one could consider derived sets even at the transfinite level: the derived set of P^(∞) could be defined as P^(∞+1) = (P^(∞))′. Cantor had discovered the infinite ordinal numbers. He did not at first recognize them as numbers, but rather regarded them as “symbols of infinity” (see Ferreirós, 1995).

44.2.2 Cardinal Numbers

Cantor was not only an analyst. He had written his dissertation under Kronecker and Ernst Eduard Kummer (1810–1893) on number-theoretic questions. Only two years after he wrote his first paper in trigonometric series, he noticed that his set-theoretic principles led to another interesting conclusion. Transcendental numbers exist. The set of algebraic numbers is a countable set (as we would now say, in the familiar language that we owe to Cantor), but the set of real numbers is not. Cantor had proved this point to his satisfaction in a series of exchanges of letters with Dedekind.

There are two versions of this proof, one due to Cantor and one due to Dedekind, but both involve getting nested sequences of closed intervals that exclude, one at a time, the elements of any given sequence {a_n} of numbers. The intersection of the intervals must then contain a number not in the sequence. In his private speculations some 40 years later, Luzin noted that Cantor was actually assuming more than the mere existence of the countable set {a_n}. In order to construct a point not in it, one had to know something about each of its elements, enough to find a subinterval of the previous closed interval that would exclude the next element. On that basis, he concluded that Cantor had proved that there was no effective enumeration of the reals, not that the reals were uncountable. Luzin thus raised the question of what it could mean for an enumeration to “exist” if it was not effective. He too delved into philosophy to find out the meaning of “existence.”

By showing in a seemingly constructive way how, given any countable enumeration of real numbers, one can exhibit a real number not in the list, Cantor had shown (he thought) that there must exist transcendental numbers. Given the complicated constructions of such numbers by Liouville and the difficulty of the proofs by Hermite and Lindemann that e and π are transcendental, this concise proof of their abstract existence seemed to have merit. The property Cantor relied on in this proof led to the concept of a cardinal number, two sets being of the same cardinality if they could be placed in one-to-one correspondence. To establish such correspondences, Cantor allowed certain methods of defining sets and functions that went beyond what mathematicians had been used to seeing. The result was a controversy that lasted some two decades.

Grattan-Guinness (2000, p. 125) has pointed out that Cantor emphasized five different aspects of point sets: their topology, dimension, measure, cardinality, and ordering. In the end, point-set topology was to become its own subject, and dimension theory became part of both algebraic and point-set topology. Measure theory became an important part of modern integration theory and had equally important applications to the theory of probability and random variables. Cardinality and ordering remained as an essential core of set theory, and the study of sets in relation to their complexity rather than their size became known as descriptive set theory.

Although descriptive set theory produces its own questions, it had at first a close relation to measure theory, since descriptive set theory was needed to specify which sets could be measured. Borel was conservative, allowing that the kinds of sets one could clearly define would have to be obtained by a finite sequence of operations, each of which was either a countable union or a countable intersection or a complementation, starting from ordinary open and closed sets. Ultimately those of a less constructive disposition than Borel honored him with the creation of the Borel sets, which is the smallest class that contains all closed subsets and also contains the complement of any of its sets and the union of any countable collection of its sets. This class, now called a σ-algebra by analysts and a σ-field by probabilists, can be “constructed” only by a transfinite induction.

Set theory, while aiming to provide a foundation of clear and simple principles for all of mathematics, soon threw up its own unanswered mathematical questions. The most prominent of these was the continuum question. Cantor had shown that the set of all real numbers could be placed in one-to-one correspondence with the set of all subsets of the integers. He denoted the cardinality of the integers as ℵ₀ and the cardinality of the real numbers as (where stands for “continuum”). The question naturally arose whether there was any subset of the real numbers that had a cardinality between these two. Cantor struggled for a long time to settle this issue. One major theorem of set theory, known as the Cantor–Bendixson theorem,⁵ after Ivar Bendixson (1861–1935), asserts that every closed set is the union of a countable set and a perfect set (a set that is equal to its derived set). Since it is easily proved that a nonempty perfect subset of the real numbers has cardinality , it follows that every uncountable closed set contains a subset of cardinality . Thus a set of real numbers having cardinality between ℵ₀ and cannot be a closed set.

Many mathematicians, especially the Moscow mathematicians after the arrival of Luzin as professor in 1915, worked on this problem. Luzin's students Pavel Sergeevich Aleksandrov (1896–1982) and Mikhail Yakovlevich Suslin (1894–1919) proved that any uncountable Borel set must contain a nonempty perfect subset and thus must have cardinality . Indeed, they proved this fact for a slightly larger class of sets called analytic sets. Luzin then proved that a set was a Borel set if and only if the set and its complement were both analytic sets.

The problem of the continuum remained open until 1938, when Kurt Gödel (1906–1978) partially closed it by showing that set theory is consistent with the continuum hypothesis and the axiom of choice,⁶ provided that it is consistent without them. Closure came to this question in 1963, when Paul Cohen (1934–2007)—like Cantor, he began his career by studying uniqueness of trigonometric series representations—showed that the continuum hypothesis and the axiom of choice are independent of the other axioms of set theory.

44.3 The Reception of Set Theory

Some mathematicians believed that set theory was an unwarranted intrusion of philosophy into mathematics. One of those was Cantor's teacher Leopold Kronecker. Although Cantor was willing to regard the existence of transcendental numbers as having been proved just because the real numbers were “too numerous” to be exhausted by the algebraic numbers, Kronecker preferred a more constructivist approach. His most famous utterance,⁷ and one of the most famous in the history of mathematics, is: “The good Lord made the integers; everything else is a human creation.” (“Die ganzen Zahlen hat der liebe Gott gemacht; alles andere ist Menschenwerk.”) That is, the only infinity he admitted was the series of positive integers 1, 2,. . .. Beyond that point, everything was human-made and therefore had to be finite. If you spoke of a number or function, you had an obligation to say how it was defined. His 1845 dissertation, which he was unable to polish to his satisfaction until 1881, when he published it as “Foundations of an arithmetical theory of algebraic quantities” in honor of his teacher Kummer, shows how conservative he was in his definitions. Instead of an arbitrary field defined axiomatically as we would now do, he wrote:

A domain of rationality is in general an arbitrarily bounded domain of magnitudes, but only to the extent that the concept permits. To be specific, since a domain of rationality can be enlarged only by the adjoining of arbitrarily chosen elements , each arbitrary extension of its boundary requires the simultaneous inclusion of all quantities rationally expressible in terms of the new element.

In this way, while one could enlarge a field to make an equation solvable, the individual elements of the larger field could still be described constructively. Kronecker's concept of a general field can be described as “finitistic.” It is the minimal object that contains the elements necessary to allow arithmetic operations. Borel took this point of view in regard to measurable sets, and Hilbert was later to take a similar point of view in describing formal languages, saying that a meaningful formula must be obtained from a specified list of elements by a finite number of applications of certain rules of combination. This approach was safer and more explicit than, for example, John Bernoulli's original definition of a function as an expression formed “in some manner” from variables and constants. The “manner” was limited in a very definite way.

44.3.1 Cantor and Kronecker

Cantor believed that Kronecker had conspired against him to delay the publication of his first paper on infinite cardinal numbers. Whether that is the case or not, it is clear that Kronecker would not have approved of some of Cantor's principles of inference. As Grattan-Guinness points out, much of what is believed about the animosity between Cantor and Kronecker is based on Cantor's own reports, which may be unreliable. Cantor was subject to periodic bouts of depression, probably caused by metabolic imbalances having nothing to do with his external circumstances. In fact, he had little to complain of in terms of the acceptance of his theories. It is true that there was some resistance to it, notably from Kronecker (until his death in 1891) and then from Poincaré. But there was also a great deal of support, from Weierstrass, Klein, Hilbert, and many others. In fact, as early as 1892, the journal Bibliotheca mathematicapublished a “Notice historique” on set theory by Giulio Vivanti (1859–1949), mentioning that there had already been several expositions of the theory, and that it was still being developed by mathematicians, applied to the theory of functions of a real variable, and studied from a philosophical point of view.

44.4 Existence and the Axiom of Choice

In the early days, Cantor's set theory seemed to allow a remarkable amount of freedom in the “construction” or, rather, the conjuring into existence, of new sets. Cantor seems to have been influenced in his introduction of the term set by an essay that Dedekind began in 1872, but did not publish until 1887 (see Grattan-Guinness, 2000, p. 104), in which he referred to a “system” as “various things a, b, c. . .comprehended from any cause under one point of view.” Dedekind defined a “thing” to be “any object of our thought.” Just as Descartes was able to conceive many things clearly and distinctly, mathematicians seemed to be able to form many “things” into “systems.” For example, given any set A, one could conceive of another set whose members were the subsets of A. This set is nowadays denoted 2^A and called the power set of A. If A has a finite number n of elements, then 2^A has 2ⁿ elements, counting the improper subsets ∅ and A.

It was not long, however, before the indiscriminate use of this freedom to form sets led to paradoxes. The most famous of these is Russell's paradox, which will be discussed in the next chapter. In modern set theory, this paradox is avoided by distinguishing between a set, which is a class that may or may not have members but at least is itself a member of some other class, and a proper class, which has members, but is not itself the member of any class. Admission to the elite company of sets is carefully controlled by the axioms. The empty class is declared to be a set by fiat. Other sets arise from operations on classes known to be sets.

One source of the paradoxes is that “existence” has a specialized mathematical meaning in set theory, which has the consequence that much of the action in a proof takes place “offstage.” That is, certain objects needed in a proof are simply declared to exist by saying, “Let there be. . .,” but no procedure for constructing them is given. Proofs relying on the abstract existence of such objects, when it is not possible to choose a particular object and examine it, became more and more common in the twentieth century. Indeed, much of measure theory, topology, and functional analysis would be impossible without such proofs. The principle behind these proofs later came to be known as Zermelo's axiom, after Ernst Zermelo (1871–1953), who first formulated it in 1904 to prove that every set could be well ordered.⁸ It was also known as the principle of free choice (in German, Auswahlprinzip) or, more commonly in English, the axiom of choice. In its broadest form this axiom states that there exists a function f defined on the class of all nonempty sets such that f(A) A for every nonempty set A. Intuitively, if A is nonempty, there exist elements of A, and f(A) chooses an element from every nonempty set A.

This axiom is used in many proofs. Probably the earliest (see Moore, 1982, p. 9) is Cantor's proof that a countable union of countable sets is countable. The proof goes as follows. Assume that A₁, A₂,. . .are countable sets, and let A= A₁∪ A₂ ∪ . Then A is countable. For, let the sets A_j be enumerated, as follows:

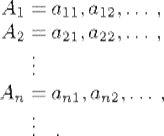
Then the elements of A can be enumerated as follows: a₁₁, a₁₂, a₂₁, a₁₃, a₂₂, a₃₁,. . ., where the elements whose ranks are larger than the triangular number T_n = n(n + 1)/2 but not larger than T_n+1 = (n + 1)(n + 2)/2 are those for which the sum of the subscripts is n + 2. There are n + 1 such elements and n + 1 such ranks. It is a very subtle point to notice that this proof assumes more than the mere existence of an enumeration of each of the sets, which is given in the hypothesis. It assumes the simultaneous existence of infinitely many enumerations, one for each set. The reasoning appears to be so natural that one would hardly question it. If a real choice exists at each stage of the proof, why can we not assume that infinitely many such choices have been made? As Moore notes, without the axiom of choice, it is consistent to assume that the real numbers can be expressed as a countable union of countable sets.⁹

Zermelo made this axiom explicit and showed its connection with ordinal numbers. The problem then was either to justify the axiom of choice, or to find a more intuitively acceptable substitute for it, or to find ways of doing without such “noneffective” concepts. A debate about this axiom took place in 1905 in the pages of the Comptes rendus of the Paris Academy of Sciences, which published a number of letters exchanged among Borel, Lebesgue, Baire, and Jacques Hadamard (1865–1963).¹⁰ Borel had raised objections to Zermelo's proof that every set could be well-ordered on the grounds that it assumed an infinite number of enumerations. Hadamard thought it an important distinction that in some cases the enumerations were all independent, as in Cantor's proof above, but in others each depended for its definition on other enumerations having been made in correspondence with a smaller ordinal number. He agreed that the latter should not be used transfinitely. Borel had objected to using the axiom of choice nondenumeratively, but Hadamard thought that this usage brought no further damage, once a denumerable infinity of choices was allowed. He also mentioned the distinction due to Jules Tannery (1848–1910) between describing an object and defining it. To Hadamard, describing an object was a stronger requirement than defining it. To supply an example for him, we might mention a well-ordering of the real numbers, which is defined by the phrase itself, but effectively indescribable. Hadamard noted Borel's own work on analytic continuation and pointed out how it would change if the only power series admitted were those that could be effectively described. The difference, he said, belongs to psychology, not mathematics.

Hadamard received a response from Baire, who took an even more conservative position than Borel. He said that once an infinite set was spoken of, “the comparison, conscious or unconscious, with a bag of marbles passed from hand to hand must disappear completely.”¹¹ The heart of Baire's objection was Zermelo's supposition that to each (nonempty) subset of a set M there corresponds one of its elements.” As Baire said, “all that it proves, as far as I am concerned, is that we do not perceive a contradiction” in imagining any set well-ordered.

Responding to Borel's request for his opinion, Lebesgue gave it. He said that Zermelo had very ingeniously shown how to solve problem A (to well-order any set) provided one could solve problem B (to choose an element from every nonempty subset of a given set). He remarked, probably with some irony, that, “Unfortunately, problem B is not easy to resolve, it seems, except for the sets that we know how to well-order.” Lebesgue mentioned a concept that was to play a large role in debates over set theory, that of “effectiveness,” roughly what we would call constructibility. He interpreted Zermelo's claim as the assertion that a well-ordering exists (that word again!) and asked a question, which he said was “hardly new”: Can one prove the existence of a mathematical object without defining it? One would think not, although Zermelo had apparently proved the existence of a well-ordering (and Cantor had proved the existence of a transcendental number) without describing it. Lebesgue and Borel preferred the verb to name (nommer) when referring to an object that was defined effectively, through a finite number of uses of well-defined operations on a given set of primitive objects.

After reading Lebesgue's opinion, Hadamard was sure that the essential distinction was between what is determined and what is described. He compared the situation with the earlier debate over the allowable definitions of a function. But, he said, uniqueness was not an issue. If one could say “For each x, there exists a number satisfying. . .. Let y be this number,” surely one could also say “For each x, there exists an infinity of numbers satisfying. . .. Let y be one of these numbers.” In that statement, he had put his finger squarely on one of the paradoxes of set theory (the Burali-Forti paradox, discussed in the next section). “It is the very existence of the set W that leads to a contradiction. . .the general definition of the word set is incorrectly applied.” What is the definition of the word set?

The validity and value of the axiom of choice remained a puzzle for some time. It leads to short proofs of many theorems whose statements are constructive. For example, it proves the existence of a nonzero translation-invariant Borel measure on any locally compact abelian group. Since such a measure is provably unique (up to a constant multiple), there ought to be effective proofs of its existence that do not use the axiom of choice (and indeed there are). One benefit of the 1905 debate was a clarification of equivalent forms of the axiom of choice and an increased awareness of the many places where it was being used. A list of important theorems whose proof used the axiom was compiled for Luzin's seminar in Moscow in 1918. The list showed, as Luzin wrote in his journal, that “almost nothing is proved without it.” Luzin was horrified, and spent some restless nights pondering the situation.

The axiom of choice is ubiquitous in modern analysis; little would remain of functional analysis or point-set topology if it were omitted entirely, although weaker assumptions might suffice. The Baire category theorem mentioned in the previous chapter cannot be proved without it. It is fortunate, therefore, that its consistency with, and independence of, the other axioms of set theory has been proved. The consequences of this axiom are suspiciously strong. In 1924 Alfred Tarski (1901–1983) and Stefan Banach (1892–1945) deduced from it that any two sets A and B in ordinary three-dimensional Euclidean space, each of which contains some ball, can be decomposed into pairwise congruent subsets. This means, for example, that a cube the size of a grain of salt (set A) and a ball the size of the sun (set B) can be written as disjoint unions of sets A₁,. . ., A_n and B₁,. . ., B_n respectively such that A_i is congruent toB_i for each i. This result (the Banach–Tarski paradox) is very difficult to accept. It can be rationalized only by realizing that the notion of existence in mathematics has no metaphysical content. To say that the subsets A_i, B_i “exist” means only that a certain formal statement beginning ∃. . . is deducible from the axioms of set theory.

Problems and Questions

Mathematical Problems

44.1. Bertrand Russell pointed out that some applications of the axiom of choice are easier to avoid than others. For instance, given an infinite collection of pairs of shoes, describe a way of choosing one shoe from each pair. Could you do the same for an infinite set of pairs of socks?

44.2. Let k = k(m) denote the largest integer less than the number

(The greatest integer less than a positive real number x can be described as [x] − [1 − x + [x]], where [x] is the standard greatest-integer function.) Show that the mapping

is an enumeration of all positive rational numbers and in fact, each positive rational number occurs an infinite number of times in this enumeration. (Show that the number occurs as f(n), where . Thus, for example, occurs at n = 8 and its reciprocal at n = 9.)

44.3. According to the axioms of set theory, every set can be well-ordered. By the continuum hypothesis, there is a one-to-one correspondence x ↔ ξ between the real numbers x such that 0 ≤ x ≤ 1 and the countable ordinal numbers ξ. Suppose such a correspondence is given and we define a function f(x, y) on pairs of real numbers between 0 and 1 by specifying that f(x, y) = 1 if ξ < υ, where x ↔ ξ and y ↔ υ, and f(x, y) = 0 otherwise. Show that

Why does this result not contradict the principal from calculus whereby a double integral can be evaluated as an iterated integral in either order. In Lebesgue integration, this principle that a double integral can be evaluated as an iterated integral still holds and is known as Fubini's theorem, after Guido Fubini (1879–1943).

Historical Questions

44.4. What was Cantor's original motive for studying sets of points on the real line?

44.5. On what philosophical grounds did Kronecker object to Cantor's methods?

44.6. What consensus did the mathematical community reach regarding set theory, especially the axiom of choice?

Questions for Reflection

44.7. In what sense do mathematical entities exist? When we prove the existence of a root of an equation or a minimal curve having a certain property without exhibiting it explicitly in terms of more familiar mathematical entities, what is the effective, practical meaning of that proof?

44.8. What does the Banach–Tarski paradox suggest about the meaning of mathematical concepts and their application to the physical world?

44.9. The philosopher Immanuel Kant (1724–1804) described mathematical knowledge (of arithmetic and geometry) as something innate, what he called synthetic, a priori knowledge. It was synthetic because propositions like the equality 5 + 7 = 12 did not follow from pure logic, that is, the definition of the concepts of 5, 7, 12, and addition. It was a priori because it was not learned from experience. We “just know” it; it's part of the way our brains are wired, as we would now say. This view, which possibly Kronecker would have agreed with, conflicts with the aims of set theory, in which arithmetic is to be derived logically from more primitive concepts. Where would you place the rock-bottom foundation layer of mathematics: in the simple arithmetic of the positive integers (with Kant and Kronecker), or in the intuitive idea of a set or class (with Cantor, Hilbert, and others)? Or is there a third possibility that seems better to you?

Notes

1. Leopold Kronecker (1823–1891) pointed out later that this assumption could be omitted. Cantor showed, as Riemann implied, that it was deducible from the mere convergence of the series.

2. Hermann Amandus Schwarz (1843–1921) later showed that if F(x) is continuous on a closed interval [a, b] and F ” _g(x) ≡ 0 on the open interval (a, b), then F(x) is linear on the closed interval [a, b].

3. A point of accumulation of a set is a point, every neighborhood of which contains infinitely many points of the set. It is also called a cluster point and (confusingly and more commonly) a limit point.

4. The word manifold (Mannigfaltigkeit) does not denote the geometric object now called a manifold. It means a multitude, which is also the earlier meaning of the English term. The modern German word for a set is Menge, also used in the phrase eine Menge von. . . to mean lots of. . .. Russian mathematicians followed this German usage and used the word mnozhestvo (multitude) to denote a set. The French use the word ensemble, which has the same connotations as the English word.

5. Ferreirós (1995) points out that it was the desire to prove this theorem adequately, in 1882, that really led Cantor to treat transfinite ordinal numbers as numbers. He was helped toward this discovery by Dedekind's pointing out to him the need to use finite ordinal numbers to define finite cardinal numbers.

6. Gödel actually included four additional assumptions in his consistency proof, one of the other two being that there exists a set that is analytic but is not a Borel set.

7. He made this statement at a meeting in Berlin in 1886 (see Grattan-Guiness, 2000, p. 122).

8. A set is well-ordered if any two elements can be compared and every nonempty subset has a smallest element. The positive integers are well ordered by the usual ordering. The positive real numbers are not, since there is no smallest positive number.

9. Not every countable union of countable sets is uncountable, however; the rational numbers remain countable, because an explicit counting function can be constructed.

10. These letters were translated into English and published by Moore (1982, pp. 311–320).

11. Luzin said essentially the same in his journal: “What makes the axiom of choice seem reasonable is the picture of reaching into a set and helping yourself to an element of it.”