The history of mathematics: A brief course (2013)

Part II. The Middle East, 2000–1500 BCE

Chapter 4. Computations in Ancient Mesopotamia

We might expect that, with their place-value system, the ancient Mesopotamians would have done arithmetic somewhat as we do. There are, however, a few differences. While we have no need to discuss addition and subtraction, we do need to compare multiplication and division in the two systems.

4.1 Arithmetic

Cuneiform tablets at the British Museum from the site of Senkereh (also known as Larsa) contain tables of products, reciprocals, squares, cubes, square roots, and cube roots of integers. It appears that the people who worked with mathematics in Mesopotamia learned by heart, just as we do, the products of all the small integers. Of course, for them a theoretical multiplication table would have to go as far as 59 × 59, and the consequent strain on memory would be large. That fact may account for the existence of so many written tables. Just as most of us learn, without being required to do so, that , the Mesopotamians wrote their fractions as sexagesimal fractions and probably came to recognize certain reciprocals, for example . With a system based on 30 or 60, all numbers less than 10 except 7 have terminating reciprocals. In order to get a terminating reciprocal for 7, one would have to go to a system based on 210, which would be far too complicated.

Even with base 60, multiplication can be quite cumbersome, and historians have conjectured that calculating devices such as an abacus might have been used, although none have been found. Hyrup (2002) has analyzed the situation by considering the errors in two problems on Old Babylonian cuneiform tablets and deduced that any such device would have had to be some kind of counting board, in which terms that were added could not be identified and subtracted again (like pebbles added to a pile).

If we try to reconstruct a base-60 multiplication using what we know of decimal multiplication, where we “carry” the tens digit to the next column to the left when the product of two digits is larger than 10, we find that it is possible to do so. However, any reasonably complicated multiplication will task the calculator's patience, since the carrying involves a sixties digit rather than a tens digit. Here is a sample multiplication that, when translated into decimal notation, verifies the computation

As you see, even without a calculator, the sexagesimal computation is only a little harder than the decimal calculation, especially since neither denominator has a terminating decimal expansion.

4.4.1 Square Roots

Not only are sexagesimal fractions handled easily in all the tablets, the concept of a square root occurs explicitly, and actual square roots are approximated by sexagesimal fractions, showing that the mathematicians of the time realized that they hadn't been able to make these square roots come out even. Whether they realized that the square root would never come out even is not clear. For example, text AO 6484 (the AO stands for Antiquités Orientales) from the Louvre in Paris contains the following problem on lines 19 and 20:

The diagonal of a square is 10 Ells. How long is the side? [To find the answer] multiply 10 by 0;42,30. [The result is] 7;5.

Now 0 ; 42, 30 is . This is the same approximation to that is found on the tablet YBC 7289, discussed in the preceding chapter. The answer 7 ; 5 is . It seems that the writer of this tablet knew that the ratio of the side of a square to its diagonal is approximately . As mentioned in the preceding chapter, the approximation to that arises from what is now called the Newton–Raphson method, starting from as the first approximation, turns up the number as the next approximation, and hence represents an approximation to .

The writers of these tablets realized that when numbers are combined by arithmetic operations, it may be of interest to know how to recover the original data from the result. This realization is the first step toward attacking the problem of inverting binary operations. Although we now handle such problems by solving quadratic equations, the Mesopotamian approach did not involve any explicit mention of equations. Instead, many of the tablets show a routine procedure, associating with a pair of numbers, say 13 and 27, two other numbers: their average (13 + 27)/2 = 20 and their semidifference¹ (27 − 13)/2 = 7. The average and semidifference can be calculated from the two numbers, and the original data can be calculated from the average and semidifference. The larger number (27) is the sum of the average and semidifference: 20 + 7 = 27, and the smaller number (13) is their difference: 20 − 7 = 13. The realization of this mutual connection makes it possible essentially to “change coordinates” from the number pair (a, b) to the pair ((a + b)/2, (a − b)/2).

At some point lost to history, some Mesopotamian mathematician came to realize that the product of two numbers is the difference of the squares of the average and semidifference: 27 · 13 = (20)² − 7² = 351 (or 5, 51 in Mesopotamian notation). This principle made it possible to recover two numbers when knowing their sum and product or knowing their difference and product. For example, given that the sum is 10 and the product is 21, we know that the average is 5 (half of the sum), hence that the square of the semidifference is 5² − 21 = 4. Therefore, the semidifference is 2, and the two numbers are 5 + 2 = 7 and 5 − 2 = 3. Similarly, knowing that the difference is 9 and the product is 52, we conclude that the semidifference is 4.5 and the square of the average is 52 + (4.5)² = 72.25. Hence the average is . Therefore, the two numbers are 8.5 + 4.5 = 13 and 8.5 − 4.5 = 4. The two techniques just illustrated occur constantly in the cuneiform texts and seem to be procedures familiar to everyone, requiring no explanation. At this point, the development of computational procedures has led to algebra, in the sense that the problems require turning an implicit definition of a number into an explicit numerical value.

The important principle here, that the difference of the squares of the average and semi-difference is the product, was to have important consequences over the next four thousand years of mathematical progress, after it was combined with the Pythagorean theorem. The principle that was in the minds of the Mesopotamian mathematicians was a two-part procedure: (1) If you are given two numbers a and b, the numbers c = (a + b)/2 (their average) and d= (a − b)/2 (their semidifference) reveal important information about them; (2) the difference of the squares of c and d is the product of a and b. In the cuneiform tablets, this principle finds algebraic application, making it possible by taking the square root to find either the average or the semidifference, provided that you know the other and that you also know their product. When combined with the Pythagorean theorem, which the Mesopotamians also knew, this “polarization principle” can lead to even more interesting new results, and did so for nearly four thousand years.

4.2 Algebra

If we interpret Mesopotamian algebra in our own terms, we can credit the mathematicians of that culture with knowing how to solve some systems of two linear equations in two unknowns, any quadratic equation having at least one real positive root, some systems of two equations where one of the equations is linear and the other quadratic, and a potentially complete set of cubic equations. Of course, it must be remembered that these people were solving problems, not equations. They did not have any classification of equations in which some forms were solvable and others not. What they knew was that they could find certain numbers from certain data. For that reason, the reader is cautioned to read the following subsection headings with reservations. The ancient mathematicians were solving problems that we now solve using algebra and classify according to these headings. They themselves must have had some other classification, since the concept of an equation did not yet exist.

4.2.1 Linear and Quadratic Problems

As just mentioned, the Mesopotamian approach to algebraic problems was to associate with every pair of numbers another pair: their average and their semidifference. These associations provide what we now call linear changes of variable. Linear problems arise frequently as a subroutine in the solution of more complex problems involving squares and products of unknowns. In Mesopotamia, what we now think of as quadratic equations occur most often as problems in two unknown quantities, usually the length and width of a rectangle. The Mesopotamian mathematicians were able to reduce a large number of problems to the form in which the sum and product or the difference and product of two unknown numbers are given. We shall consider an example that has been written about by many authors. It occurs on a tablet from the Louvre in Paris, known as AO 8862.

A loose translation of the text of this tablet, made from Neugebauer's German translation, reads as follows:

I have multiplied the length and width so as to make the area. Then I added to the area the amount by which the length exceeds the width, obtaining 3,3. Then I added the length and width together, obtaining 27. What are the length, width, and area?

You proceed as follows:

Add the sum (27) of the length and width to 3,3. You thereby obtain 3,30. Next add 2 to 27, getting 29. You then divide 29 in half, getting 14;30. The square of 14;30 is 3,30;15. You subtract 3,30 from 3,30;15, leaving the difference of 0;15. The square root of 0;15 is 0;30. Adding 0;30 to the original 14;30 gives 15, which is the length. Subtracting 0;30 from 14;30 gives 14 as width. You then subtract 2, which was added to the 27, from 14, giving 12 as the final width.

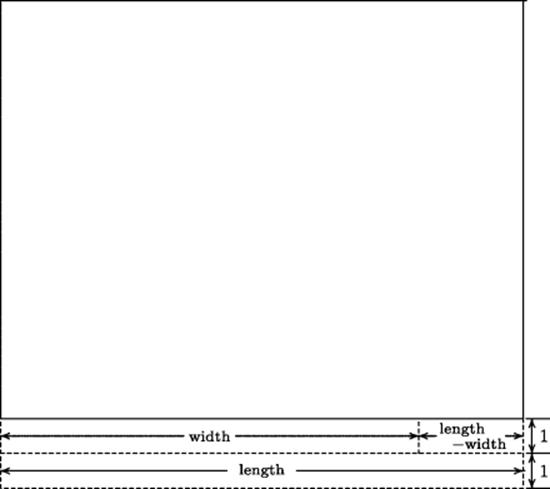
The author continues, verifying that these numbers do indeed solve the problem. This text requires some commentary, since it is baffling at first. Knowing the general approach of the Mesopotamian mathematicians to problems of this sort, one can understand the reason for dividing 29 in half (so as to get the average of two numbers) and the reason for subtracting 3,30 from the square of 14;30 (the difference between the square of the average and the product will be the square of the semidifference of the two numbers whose sum is 29 and whose product is 3,30, that is, 210). What is not clear is the following: Why add 27 to the number 3,3 in the first place, and why add 2 to 27? Possibly the answer is contained in Fig. 4.1, which shows that adding the difference between length and width to the area amounts to gluing a smaller rectangle of unit width onto the rectangle whose dimensions are to be found. Then adding the sum of length and width amounts to gluing a gnomon onto the resulting figure in order to complete a rectangle two units wider than the original. Finding the dimensions of that rectangle from its perimeter and area is the standard technique of solving a quadratic equation, and that is what the author does. It is not clear that this gluing of additions onto the rectangle represents the thought process of the original author. The present author finds this very plausible, but it is worth noting that van der Waerden (1963) insisted that the original author was actually carrying out the mathematically absurd operation of adding length to area. On those grounds, he concluded that “we may safely set this down as a pair of equations in two unknowns.”²

Figure 4.1 Reduction of a problem to standard form.

The tablet AO 6670, as explicated by van der Waerden (1963, pp. 73–74), involves two unknowns and two conditions, given in abstract terms without specific numbers. Unfortunately, the explanation is very difficult to understand. The statement of the problem is taken directly from Neugebauer's translation: Length and width as much as area; let them be equal. Thereafter, the translation given by van der Waerden, due to François Thureau-Dangin (1872–1944), goes as follows:

The product you take twice. From this you subtract 1. You form the reciprocal. With the product that you have taken you multiply, and the width it gives you.

Van der Waerden asserts that the formula y = (1/(x − 1)) · x is “stated in the text” of Thureau-Dangin's translation. If so, it must have been stated in a place not quoted by van der Waerden, since x is not a “product” here, nor is it taken twice. Van der Waerden also notes that according to Evert Marie Bruins (1909–1990), the phrase “length and width” does not mean the sum of length and width. Van der Waerden says that “the meaning of the words has to be determined in relation to the mathematical content.” The last two sentences in the description tell how to determine the width once the length has been found. That is, you take the reciprocal of the length and multiply it by the product of length and width, which must be given in the problem as the area. The mystery is then pushed into the first two instructions. What product is being “taken twice”? Does taking a product twice mean multiplying by 2, or does it mean cubing? Why is the number 1 being subtracted? Perhaps we should go back to the original statement and ask whether “as much as area” implies an equation, or whether it simply means that length and width form an area. What does the word them refer to in the statement, “Let them be equal”? Is it the length and the width, or some combination of them and the area? Without knowing the original language and seeing the original text, we cannot do anything except suggest possible meanings, based on what is mathematically correct, to those who do know the language.

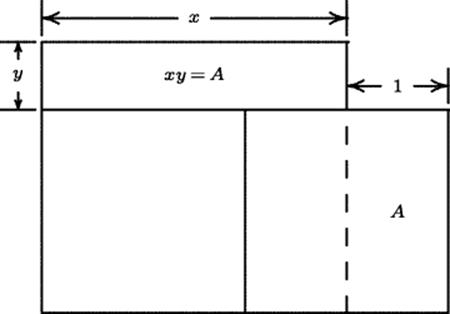
We can get a geometric problem that fits this description by considering Fig. 4.2, where two equal squares have been placed side by side and a rectangle of unit length, shown by the dashed line, has been removed from the end. If the problem is to construct a rectangle on the remaining base equal to the part that was cut off, we have conditions that satisfy the instructions in the problem. That is, the length x of the base of the new rectangle is obtained numerically by subtracting 1 from twice the given area. Still, it is dangerous for any nonspecialist to speculate about the meaning without being able to read the original document, and it is probably best to leave this problem at this point.

Figure 4.2 A scenario that may “fit” a text from cuneiform tablet AO 6670.

4.2.2 Higher-Degree Problems

Cuneiform tablets have been found—one such being VAT 8402, for example³ [see Neugebauer (1935, p. 76)]—that give the sum of the square and cube of an integer for many values of the integer. These tablets may have been used for finding the numbers to which this operation was applied in order to obtain a given number. In modern terms these tablets make it possible to solve the equation x³ + x² = a, a difficult problem to attack directly, being in principle just as difficult as solving the general cubic equation. However, that was probably not the purpose of the tablet, which remains a mystery.

Neugebauer (1935, p. 99; 1952, p. 43) reports that the Mesopotamian mathematicians moved beyond algebra proper and investigated the laws of exponents, compiling tables of successive powers of numbers and determining the power to which one number must be raised in order to yield another. Such problems occur in a commercial context, involving compound interest. For example, the tablet AO 6484 gives the sum of the powers of 2 from 0 to 9 as the last term plus one less than the last term, as well as the sum of the squares of the first segment of integers as the sum of the same integers multiplied by the sum of the number and of the last integer in the segment. This recipe is equivalent to the modern formula for the sum of the squares of the first n integers. That is,

Problems and Questions

Mathematical Problems

4.1. Find the product 37 ; 11, 7 × 6, 13 ; 41 through standard multiplication.

4.2. Find two numbers whose sum is 15 and whose product is 40.25 by following the standard Mesopotamian technique of forming the average and semidifference.

4.3. Find two numbers whose difference is 4 and whose product is using the standard Mesopotamian technique.

Historical Questions

4.4. In what sense did the Mesopotamian authors “do algebra”? Did they have the concept of an equation or a classification of types of equations?

4.5. Give an example of a mathematical technique developed in Mesopotamia and extended to solve problems more general than the model on which it is based.

4.6. How did the Mesopotamian mathematicians deal with irrational square roots?

Questions for Reflection

4.7. For what purpose is it important to be able to find two numbers given their sum and product? Is there any practical application of this technique in everyday life?

4.8. For what purpose might a person need a table giving the sum of the cube and square of various numbers? Obviously, this table had some purpose, but was it perhaps simply an exercise in arithmetic for a pupil learning how to calculate? The expression can be interpreted geometrically, but does this geometric interpretation suggest any application?

4.9. The power of modern mathematical methods is so fascinating that there is a strong temptation to apply them to ancient texts. With our algebraic notation, we can reduce every cubic equation ax³ + bx² + cx + d = 0 to an equation of the form y³ + y² = A. Give at least two reasons why it is not plausible that the table of such values found on the tablet VAT 8402 had this purpose. [Hint: The transformation that brings about this reduction is the fractional-linear substitution . Here . (If you feel like verifying this fact, a computer algebra program such as Mathematica will help.)]

Notes

1. This word is coined because English contains no one-word description of this concept, which must otherwise be described as half of the difference of the two numbers. It is clear from the way in which the semidifference occurs constantly that the writers of these tablets automatically looked at this number along with the average when given two numbers as data. There seems to be no word in the Akkadian, Sumerian, and ideogram glossary given by Neugebauer to indicate that the writers of the clay tablets had a special word for these concepts. It seems clear, however, that the scribes were trained to calculate these numbers when dealing with this type of problem. In the translations given by Neugebauer, the average and semidifference are obtained one step at a time, by first adding or subtracting the two numbers and then taking half of the result.

2. Van der Waerden also argued that the words for length and width (uš and šag), being indeclinable, were being used as symbols for an abstract unknown quantity. The choice is stark: We must conclude that the scribe either was using a kind of linguistic shorthand in which a length becomes a rectangle of unit width or was a modern algebraist for whom dimensional consistency is of no importance.

3. VAT stands for Vorderasiatisches (Near East) Museum, in Berlin, part of the Pergamon Museum.