The history of mathematics: A brief course (2013)

Part II. The Middle East, 2000–1500 BCE

Chapter 5. Geometry in Mesopotamia

Mesopotamian geometry was mostly concerned with the measurement of length, area, and volume. Still, many of the problems that are posed in geometric garb have no apparent practical application but are very good exercises in computation. For example, the Old Babylonian tablet BM 13901 contains the following problem: Given two squares such that the side of one is two-thirds that of the other plus 5 GAR and whose total area is 25,25 square GAR, what are the sides of the squares? Where in real life would one encounter such a problem? The tablet itself gives no practical context, and we conclude that this apparently geometric problem is really a computational problem. Earlier historians may have carried this idea too far. Neugebauer (1952, p. 41) stated, “It is easy to show that geometrical concepts play a very secondary part in Babylonian algebra, however extensively a geometrical terminology may be used.” Both Neugebauer and van der Waerden (1963, p. 72) point out that the cuneiform tablets contain operations that are geometrically absurd, such as adding a length to an area or multiplying two areas. These two giant figures in the history of mathematics a half century ago may have been too eager to press modern notions down on documents from the past. The very use of the word algebra tends to be misleading, since it suggests manipulation of symbols rather than numbers and the writing of equations, both of which are absent from the cuneiform tablets. Hyrup, one of the leading experts in this area, denies that any such dimensional inconsistency occurs, stating (2010, p. 5) that “No Babylonian text ever adds a number and either a length or an area.” His research (see Robson, 2009, p. 7), confirms that the numbers found in the geometric tablets are what we call concrete numbers, having a physical dimension like length or area.

5.1 The Pythagorean Theorem

There is conclusive evidence that the Mesopotamians knew the Pythagorean theorem at least 1000 years before Pythagoras (who, as we shall see, may have had nothing at all to do with it). They were thus already on the road to finding more abstract properties of geometric figures than mere size. This theorem was known at an early date in India and China, so that one cannot say certainly where the earliest discovery was and whether the appearance of this theorem in different localities was the result of independent discovery or transmission. But as far as present knowledge goes, the earliest examples of the use of the “Pythagorean” principle that the square of the hypotenuse of a right triangle equals the sum of the squares of the other two legs occur in the cuneiform tablets. The Old Babylonian text known as BM 85196 contains a problem that has appeared in algebra books for centuries, the “leaning-ladder” problem, in which a ladder 30 units long is leaning against a wall, its top being 6 units below where it would be if pressed flush against the wall. The student is supposed to find how far away from the wall the bottom of the ladder is. In this problem we are dealing with a right triangle of hypotenuse 30 with one leg equal to 30 − 6 = 24. Obviously, this is the famous 3–4–5 right triangle with all sides multiplied by 6. Obviously also, the interest in this theorem was more numerical than geometric. How often, after all, are we called upon to solve problems of this type in everyday life?

How might the Pythagorean theorem have been discovered? The following hypothesis was presented by Allman (1889, pp. 35–37), who cited a work (1870) by Carl Anton Bretschneider (1808–1878). Allman thought this dissection was due to the Egyptians, since, he said, it was done in their style.

Suppose that you find it necessary to construct a square twice as large as a given square. How would you go about doing so? (This is a problem the Platonic Socrates poses in the dialogue Meno.) You might double the side of the square, but you would soon realize that doing so actually quadruples the size of the square. If you drew out the quadrupled square and contemplated it for a while, you might be led to join the midpoints of its sides in order, that is, to draw the diagonals of the four copies of the original square. Since these diagonals cut the four squares in half, they will enclose a square twice as big as the original one (Fig. 5.1a). It is quite likely that someone, either for practical purposes or just for fun, discovered this way of doubling a square. If so, someone playing with the figure might have considered the result of joining in order the points at a given distance from the corners of a square instead of joining the midpoints of the sides. Doing so creates a square in the center of the larger square surrounded by four copies of a right triangle whose hypotenuse equals the side of the center square (Fig. 5.1b); it also creates the two squares on the legs of that right triangle and two rectangles that together are equal in area to four copies of the triangle. (In Fig. 5.1b, one of these rectangles is divided into two equal parts by its diagonal, which is the hypotenuse of the right triangle.) Hence the larger square consists of four copies of the right triangle plus the center square. It also consists of four copies of the right triangle plus the squares on the two legs of the right triangle. The inevitable conclusion is that the square on the hypotenuse of any right triangle equals the sum of the squares on the legs. This is the Pythagorean theorem, and it is used in many places in the cuneiform texts.

Figure 5.1 (a) Doubling a square; (b) the Pythagorean theorem.

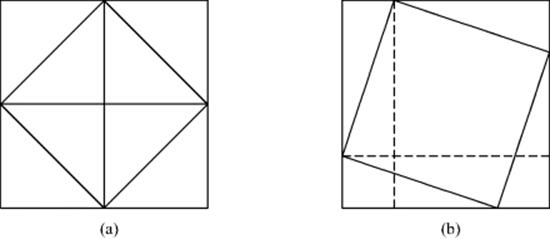
Given that they knew the Pythagorean principle and also the polarization identity that makes it possible to express the product of two numbers as a difference of squares, it seems remarkable that the Mesopotamian mathematicians did not combine the two. If the hypotenuse of a right triangle is the average of two lengths and one of the legs is the semidifference, then the square on the other leg is the difference of the squares of the average and semidifference and, hence, is equal to the rectangle on the original two lengths. In this way, one can turn any rectangle into a square. The ingredients of a tasty mathematical dish were all there, but it does not appear that the Mesopotamians combined them and made them into a meal. It was left to the early Greeks to do that.

5.2 Plane Figures

Some cuneiform tablets give the area of a circle in a way that we would interpret as implying π = 3. That statement, however, may mislead, since the procedure used for finding the area was not to multiply the square on the radius by a number, as we do, but to divide the square on the circumference by a number. That divisor needs to be 4π in our terms, and it appears to be 12 on at least one tablet. Hence the misleading shorthand that π = 3. On the other hand (Neugebauer, 1952, p. 46), the ratio of the circumference to the diameter, which we are going to call one-dimensional π,¹ was given with more precision. On a tablet excavated at Susa in 1936, it was stated that the perimeter of a regular hexagon, which is three times its diameter, is 0 ; 57, 36 times the circumference of the circumscribed circle. That makes the circumference of a circle of unit diameter equal to

That the Mesopotamian mathematicians saw a relation between the area and the circumference of a circle is shown by two Old Babylonian tablets from the Yale Babylonian Collection (YBC 7302 and YBC 11120, see Robson, 2001, p. 180). The first contains a circle with the numbers 3 and 9 on the outside and 45 on the inside. These numbers fit perfectly the formula A = C²/(4π), given that the scribe was using π = 3. Assuming that the 3 represents the circumference, 9 its square, and 45 the quotient, we find 9/(4 · 3) = 3/4 = 0 ; 45. Confirmation of this hypothesis comes from the other tablet, which contains 1 ; 30 outside and 11 ; 15 inside, since (1 ; 30²)/(4 · 3) = (2 ; 15)/12 = 135/12 = 11.25 = 11 ; 15.

5.2.1 Mesopotamian Astronomy

The strongest area of Mesopotamian science that has been preserved is astronomy, and it is here that geometry becomes most useful. The measurement of angles—arcs of circles—is essential to observation of the sun, moon, stars, and planets, since to the human eye they all appear to be attached to a large sphere rotating overhead. The division of a circle into 360 degrees is one convention that came from Mesopotamia, was embraced by the Greeks, and became an essential part of applied geometry down to the present day. The reason for the number 360 is the base-60 computational system used in Mesopotamia. The astronomers divided all circles into 360 or 720 equal parts and divided the radius into 60 equal parts. In that way, a unit of length along the radius was approximately equal to a unit of length on the circle.

5.3 Volumes

The cuneiform tablets contain computations of the volumes of some simple solid figures. For example, the volume of a frustum of a square pyramid is computed in an Old Babylonian tablet (BM 85194). The Mesopotamian scribe seems to have generalized incorrectly from the case of a trapezoid and reasoned that the volume is the height times the average area of the upper and lower faces. This rule overestimates the volume. There is, however, some disagreement as to the correct translation of the tablet in question. Neugebauer (1935, Vol. 1, p. 187) claimed that the computation was based on an algebraic formula that is geometrically correct. The square bases are given as having sides 10 and 7, respectively, and the height is given as 18. The incorrect rule just mentioned would give a volume of 1341, which is 22,21 in sexagesimal notation; but the actual text reads 22,30. The discrepancy could be a simple misprint, with three ten-symbols carelessly written for two ten-symbols and a one-symbol. The computation used is not entirely clear. The scribe first took the average base side (10 + 7)/2 and squared it to get 1, 12 ; 15 in sexagesimal notation (72.25). At this point there is apparently some obscurity in the tablet itself. Neugebauer interpreted the next number as 0; 45, which he assumed was calculated as one-third of the square of (10 − 7)/2. The sum of these two numbers is 1, 13, which, multiplied by 18, yields 21, 54 (that is, 1314), which is the correct result. But it is difficult to see how this number could have been recorded incorrectly as 22, 30. If the number that Neugebauer interprets as 0 ; 45 is actually 2; 15 (which is a stretch—three ten-symbols would have to become two one-symbols), it would be exactly the square of (10 − 7)/2, and it would yield the same incorrect formula as the assumption that the average of the areas of the two bases was being taken. In any case, the same procedure is used to compute the volume of the frustum of a cone (Neugebauer, 1935, p. 176), and in that case it definitely is the incorrect rule stated here, taking the average of the two bases and multiplying by the height.

5.4 Plimpton 322

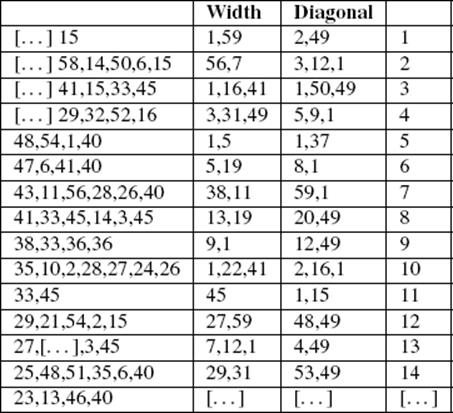
The diagonals and sides of rectangles are the subject of a cuneiform tablet from the period 1900–1600 BCE, number 322 of the Plimpton collection at Columbia University. The numbers on this tablet have intrigued many mathematically oriented people, leading to a wide variety of speculation as to the original purpose of the tablet.

Plimpton 322. © Rare Book and Manuscript Library, Columbia University.

As you can see from the photograph, there are a few chips missing, so that some of the cuneiform numbers in the tablet will need to be restored by plausible conjecture. Notice also that the column at the right-hand edge contains the cuneiform numbers in the sequence 1, 2, 3, 4,. . .,. . ., 7, 8, 9, 10, 11, 12, 13,. . .,. . .. Obviously, this column merely numbers the rows. The column second from the right consists of identical symbols that we shall ignore entirely. Pretending that this column is not present, if we transcribe only what we can see into our version of sexagesimal notation, denoting the chipped-off places with brackets ([. . .]), we get the four-column table shown below.

Before analyzing the mathematics of this table, we make one preliminary observation: Row 13 is anomalous, in that the third entry is smaller than the second entry. For the time being, we shall ignore this row and see if we can figure out how to correct it. Row 15 (the bottom row) is damaged, and we shall temporarily exclude it from consideration. Since the long numbers in the first column must be the result of computation—it is unlikely that measurements could be carried out with such precision—we make the reasonable conjecture that the shorter numbers in the second and third columns are data. As mentioned in the preceding chapter, the Mesopotamian mathematicians routinely associated with any pair of numbers (a, b) two other numbers: their average (a + b)/2 and their semidifference (b − a)/2. Let us compute these numbers for all the rows except rows 13 and 15 to see how they would have appeared to a mathematician of the time. We get the following 13 pairs of numbers, which we write in decimal notation: (144, 25), (7444, 4077), (5625, 1024), (15625, 2916), (81, 16), (400, 81), (2916, 625), (1024, 225), (655, 114), (6561, 1600), (60, 15), (2304, 625), (2500, 729).

You will probably recognize a large number of perfect squares in the table. Indeed, all of these numbers, except for those corresponding to rows 2, 9, and 11, are perfect squares: 10 pairs of perfect squares out of thirteen! That is too unusual to be a mere coincidence. A closer examination reveals that they are squares of numbers whose only prime factors are 2, 3, and 5. Now these are precisely the prime factors of the number 60, which the Mesopotamian mathematicians used as a base. That means that the reciprocals of these numbers will have terminating sexagesimal expansions. We should therefore keep in mind that the reciprocals of these numbers may play a role in the construction of the table.

Notice also that these ten pairs are all relatively prime pairs. Let us now denote the square root of the average by p and denote the square root of the semidifference by q. Column 2 will then be p² − q², and column 3 will be p² + q². Having identified the pairs (p, q) as important clues, we now ask which pairs of integers occur here and how they are arranged. The values of q, being smaller, are easily handled. The smallest q that occurs is 5 and the largest is 54, which also is the largest number less than 60 whose only prime factors are 2, 3, and 5. Thus, we could try constructing such a table for all values of q less than 60 having only those prime factors. But what about the values of p? Again, ignoring the rows for which we do not have a pair (p, q), we observe that the rows occur in decreasing order of p/q, starting from 12/5 = 2.4 and decreasing to 50/27 = 1.85185185. . . . Let us then impose the following conditions on the numbers p and q:

1. The integers p and q are relatively prime.

2. The only prime factors of p and q are 2, 3, and 5.

3. q < 60.

4. 1.8 ≤ p/q ≤ 2.4

Now, following an idea of Price (1964), we ask which possible (p, q) satisfy these four conditions. We find that every possible pair occurs with only five exceptions: (2, 1), (9, 5), (15, 8), (25, 12), and (64, 27). There are precisely five rows in the table—rows 2, 9, 11, 13, and 15—for which we did not find a pair of perfect squares. Convincing proof that we are on the right track appears when we arrange these pairs in decreasing order of the ratio p/q. We find that (2, 1) belongs in row 11, (9, 5) in row 15, (15, 8) in row 13, (25, 12) in row 9, and (64, 27) in row 2, precisely the rows for which we did not previously have a pair p, q. The evidence is overwhelming that these rows were intended to be constructed using these pairs (p, q). When we replace the entries that we can read by the corresponding numbers p² − q² in column 2 and p² + q² in column 3, we find the following:

In row 2, the entry 3,12,1 has to be replaced by 1,20,25, that is, 11521 becomes 4825. The other entry in this row, 56,7, is correct.

In row 9, the entry 9,1 needs to be replaced by 8,1, so here the writer simply inserted an extra unit character.

In row 11, the entries 45 and 75 must be replaced by 3 and 5; that is, both are divided by 15. It has been remarked that if these numbers were interpreted as 45 · 60 and 75 · 60, then in fact, one would get p = 60, q = 30, so that this row was not actually “out of step” with the others. But of course when that interpretation is made, p and q are no longer relatively prime, in contrast to all the other rows.

In row 13 the entry 7,12,1 must be replaced by 2,41; that is, 25921 becomes 161. In other words, the table entry is the square of what it should be.

The illegible entries in row 15 now become 56 and 106. The first of these is consistent with what can be read on the tablet. The second tablet entry appears to be 53, half of what it should be.

The final task in determining the mathematical meaning of the tablet is to explain the numbers in the first column and interpolate the missing pieces of that column. Notice that the second and third columns in the table are labeled “width” and “diagonal.” Those labels tell us that we are dealing with dimensions of a rectangle here and that we should be looking for its length. By the Pythagorean theorem, that length is . Even with this auxiliary number, however, it requires some ingenuity to find a formula involving p and q that fits the entries in the first column that can be read. If the numbers in the first column are interpreted as the sexagesimal representations of numbers between 0 and 1, those in rows 5 through 14—the rows that can be read—all fit the formula²

Assuming this interpretation, since it works for the 10 entries we can read,³ we can fill in the missing digits in the first four and last rows. This involves adding one or two digits to the beginning of the first four rows, and it appears that there is just the right amount of room in the chipped-off place to allow this to happen.⁴ The digits that occur in the bottom row are 23,13,46,40, and they are consistent with the parts that can be read from the tablet itself.

5.4.1 The Purpose of Plimpton 322: Some Conjectures

The structure of the tablet is no longer a mystery, except for the tiny mystery of the misprint in row 2, column 3. Its purpose, however, is not clear. What information was the table intended to convey? Was it intended to be used as people once used tables of products, square roots, and logarithms—that is, to look up a number or pair of numbers? If so, which columns contained the input and which the output? One geometric problem that can be solved by use of this tablet is that of multiplying a square by a given number; that is, given a square of side a, it is possible to find the side b of a square whose ratio to the first square is given in the first column. To do so, take a rope whose length equals the side a and divide it into the number of equal parts given in the second column, then take a second rope with the same unit of length and total length equal to the number of units in the third column and use these two lengths to form a leg and the hypotenuse of a right triangle. The other leg will then be the side of a square having the given ratio to the given square. The problem of shrinking or enlarging squares was considered in other cultures, but such an interpretation of Plimpton 322 has only the merit that there is no way of proving the tablet wasn't used in this way. There is no proof that the tablet was ever put to this use.

Friberg (1981) suggested that the purpose of the tablet was trigonometrical—that is, that it was a table of squares of tangents. Columns 2 and 3 give one leg and the hypotenuse of 15 triangles with angles intermediate between those of the standard 45–45–90 and 30–60–90 triangles. What is very intriguing is that, if this was its purpose, the table covers the case of all possible triangles whose shapes are between these two and whose legs have lengths that are multiples of a standard unit by numbers having only 2, 3, and 5 as factors. Of all right triangles, the 45–45–90 and the 30–60–90 are the two that play the most important role in all kinds of geometric applications; plastic models of them were once used as templates in mechanical drawing, and such models are still sold. It is easy to imagine that a larger selection of triangle shapes might have been useful in the past, before modern drafting instruments and computer-aided design. Using this table, one could build 15 model triangles with angles varying in increments of approximately 1°. One can imagine such models being built and the engineer of 4000 years ago reaching for a “number 7 triangle” when a slope of 574/675 = . 8504 was needed. However, this scenario still lacks plausibility. Even if we assume that the engineer kept the tablet around as a reference when it was necessary to know the slope, the tablet stores the square of the slope in column 1. It is difficult to imagine any engineering application for that number.

We now explore the computational and pedagogical possibilities inherent in this tablet. The left-hand column contains numbers that are perfect squares and remain perfect squares when 1 is added to them. If the purpose of the table was to generate numbers with this property, the use of the table would be as follows: Square the entry in column 3, square the entry in column 2, and then divide each by the difference of these squares. The results of these two divisions would be two squares differing by 1. The numbers p and q that generate the two columns can be arbitrary, but in order to get a sexagesimally terminating entry in the first column, the difference (p² + q²)² − (p² − q²)² = 4p²q² should have only 2, 3, and 5 as prime factors, and hence p and q also should have only these factors. Against this interpretation there lies the objection that p and q are concealed from the casual reader of the tablet.

In a paper that was never published (see Buck, 1980, p. 344), D. L. Voils⁵ pointed out that tablets amounting to “teacher's manuals” have been found in which the following problem is set: Find a number that yields a given number when its reciprocal is subtracted. In modern terms, this problem requires solving the equation

where d is the given number. Obviously, if you were a teacher setting such a problem for a student, you would want the solution x to be such that both x and 1/x have terminating sexagesimal digits. So, if the solution is to be x = p/q, we already see why we need both p and q to be products of 2, 3, and 5. This problem amounts to the quadratic equation x² − dx − 1 = 0, and its unique positive solution is . Column 1 of the tablet, which contains (d/2)², then appears as part of the solution process. It is necessary to take its square root and also the square root of (which is the same number with a 1 prefixed to it) in order to find the solution x = p/q. This explanation seems to fit very well with the tablet. One could assume that the first column gives values of d that a teacher could use to set such a problem with the assurance that the pupil would get terminating sexagesimal expansions for both x and 1/x. This hypothesis also fits very well with the fact already noted that many of the cuneiform tablets are pedagogical in nature. On the other hand, it does not fully explain why the tablet gives the numbers p² − q² and p² + q², rather than simply p and q, in subsequent columns. Doing our best for this theory, we note that columns 2 and 3 contain, respectively, the numerators of x − 1/x and x + 1/x and that their common denominator is the square root of the difference of the squares of these two numerators. Against that explanation is the fact that the Mesopotamians did not work with common fractions. The concepts of numerator and denominator to them would have been the concepts of dividend and divisor, and the final sexagesimal quotient would not display these numbers. Still, a terminating sexagesimal expansion is a common fraction, and these special numbers (the only numbers ever considered in Mesopotamia) amount to the use of common fractions, confined to those whose denominators are products of powers of 2, 3, and 5. The recipe for getting from columns 2 and 3 to column 1 would be first to square each of these columns, then find the reciprocal of the difference of the squares as a sexagesimal expansion, and, finally, multiply the last result by the square in column 2.

Problems and Questions

Mathematical Problems

5.1. Explain the author's solution of the “leaning-ladder” problem from the cuneiform tablet BM 85196. Here the numbers in square brackets were worn off the tablet and have been reconstructed.

A beam of length 0;30 GAR [about 3 meters] is leaning against a wall. Its upper end is 0;6 GAR lower than it would be if it were perfectly upright. How far is its lower end from the wall?

Do the following: Square 0;30, obtaining 0;15. Subtracting 0;6 from 0;30 leaves 0;24. Square 0;24, obtaining 0;9,36. Subtract 0;9,36 from [0;15], leaving 0;5,24. What is the square root of 0;5,24? The lower end of the beam is [0;18] from the wall.

When the lower end is 0;18 from the wall, how far has the top slid down? Square 0;18, obtaining 0;5;24. . . .

5.2. Show that the average of the areas of the two bases of a frustum of a square pyramid is the sum of the squares of the average and semidifference of the sides of the bases.

5.3. Solve the problem from BM 13901, finding two squares, one of which has a side five units longer than the other and whose total area is 25, 25 square units.

Historical Questions

5.4. From which time period and dynasty do the Old Babylonian tablets come?

5.5. What standard geometric figures are studied in the Old Babylonian tablets discussed in this chapter?

5.6. Why is it misleading to talk about the “Babylonian value of π”?

Questions for Reflection

5.7. In what everyday applications might some of the geometric problems discussed above (such as finding the volume of a frustum of a pyramid) be useful?

5.8. Could the relation noted above between the areas of the two bases of a frustum of a square pyramid and the squares of the average and semidifference of their sides have led the Mesopotamian mathematicians astray in their computation of the volume of the frustum?

5.9. Given that it is difficult to think of applications of the many geometric problems studied in the tablets, what could have been the motive for writing them?

Notes

1. We use this term to specify the ratio of the circumference to the diameter of a circle. The geometric fact that this ratio is the same for all circles is taken for granted. What we shall call two-dimensionalπ is the ratio of the area enclosed by a circle to the interior of the square on its radius. Again, it is taken for granted that this ratio is the same for all circles. The reader can formulate the definition of three-dimensional π. That these ratios are all the same real number is not obvious, but seems to have been known even by ancient peoples.

2. In some discussions of Plimpton 322 the claim is made that a sexagesimal 1 should be placed before each of the numbers in the first column. Although the tablet is clearly broken off on the left, it does not appear from pictures of the tablet—the author has never seen it “live”—that there were any such digits there before. Neugebauer (1952, p. 37) claims that parts of the initial 1 remain from line 4 on “as is clearly seen from the photograph” and that the initial 1 in line 14 is completely preserved. When that assumption is made, however, the only change in the interpretation is a trivial one: The negative sign in the formula must be changed to a positive sign, and what Friberg interpreted as a column of squares of tangents becomes a column of squares of secants, since tan ²θ + 1 = sec ²θ.

3. Comparing the original in the photograph with the computed values in the first column of the table, it appears that the original tablet has the single digit 59 in the middle of Column 1 of row 8 instead of the computed digits 45, 14 which we entered in the table. This seeming discrepancy—if it is a discrepancy—is easily explained by assuming that the scribe simply merged the two sexagesimal digits, which have a total of five 10-symbols and nine 1-symbols between them.

4. The digits to be inserted are as follows. Row 1: 59, 0 (but the zero would have been a blank space in the original). Row 2: 56, 56. Row 3: 55, 7. Row 4: 53, 10.

5. In early 2011, Prof. Douglas Rogers of the University of Hawaii made a diligent search and located Voils, now retired in Florida. Voils reported that he had indeed written such a paper, but declined to revise it for publication, since his interest had shifted to computer science.