The history of mathematics: A brief course (2013)
Part II. The Middle East, 2000–1500 BCE
Chapter 6. Egyptian Numerals and Arithmetic
The earliest systematic treatises on mathematics come from the Egyptian civilization, which was already 2000 years old before the mathematical treatises that survive today were written. After several thousand years during which the area now called Egypt was the home of isolated agricultural communities, a process of consolidation began, and by 3100 BCE there were two major kingdoms, Upper Egypt in the south and Lower Egypt in the north. Egypt became politically unified about this time when a ruler of Upper Egypt, variously said to be named Menes, Narmer, or “Scorpion,” conquered Lower Egypt. In the four centuries following this conquest, a number of technological advances were made in Egypt, making it possible to undertake large-scale engineering projects. Such projects required a certain amount of arithmetic and geometry. Shortly after the beginning of the Old Kingdom (2685 BCE) the famous Step Pyramid of Djoser was built, the first structure made entirely of hewn stone. The Old Kingdom, which lasted just over five centuries, was a time of active building of temples and tombs. The collapse of central authority at the end of this period led to a century and a half during which the real power was held by provincial governors. The central authority recovered when the governors of Thebes extended their power northward and over several generations brought about the Middle Kingdom (2040–1785 BCE).
When the central authority weakened again at the end of this period, foreign invaders known as the Hyksos conquered most of Egypt from the north. The Hyksos rule lasted for about a century, until some of their puppet governors became strong enough to usurp their authority; the Hyksos were driven out in 1570 BCE, which marked the beginning of the New Kingdom. It was during the Hyksos period that the earliest mathematical treatises still extant were written. We therefore begin with a discussion of mathematics as practiced in the Middle Kingdom.
6.1 Sources
Mathematics has been practiced in Egypt continuously starting at least 4000 years ago. Aristotle believed that the study of mathematics first arose among the Egyptians. In his Metaphysics (Bekker1 981b), he wrote
Thus it was that the mathematical sciences first arose in Egypt. For it was there that the priestly caste was granted the necessary leisure.
In the late fourth century BCE, it merged with the mathematics of the Greeks, who had learned the basics of geometry from the Egyptians. Indeed, the intellectual center of the Western world, the city of Alexandria founded by Alexander the Great, was in Egypt. Centuries later, Egypt formed part of the Muslim culture centered in Baghdad, which also produced some brilliant mathematics, and mathematical creativity continues in Egypt at the present day. The Egyptian mathematics we are going to discuss, however, had a beginning and an end. It began with hieroglyphic inscriptions containing numbers and dating to the third millennium BCE and ended at the time of Euclid, in the third century BCE. After that time, the city of Alexandria in the Nile delta was the main school of mathematics in the Hellenistic world, and many of the most prominent mathematicians who wrote in Greek studied there. We shall confine our attention, however, to what was for many centuries the standard set of mathematical techniques used by the professionals who administered the Egyptian state during the Middle Kingdom.
6.1.1 Mathematics in Hieroglyphics and Hieratic
The great architectural monuments of ancient Egypt are covered with hieroglyphic characters, some of which contain numbers. In fact, the ceremonial mace of the founder of the first dynasty contains records that mention oxen, goats, and prisoners and contain hieroglyphic symbols for the numbers 10,000, 100,000, and 1,000,000. These hieroglyphic symbols, although suitable for ceremonial recording of numbers, were not well adapted for writing on papyrus or leather. The language of the earliest written documents that have been preserved to the present time is a cursive known as hieratic.
The most detailed information about Egyptian mathematics comes from a single document written in the hieratic script on papyrus around 1650 BCE and preserved in the dry Egyptian climate. This document is known as the Rhind papyrus, after the British lawyer Alexander Rhind (1833–1863), who went to Egypt for his health and became an Egyptologist. Rhind purchased the papyrus in Luxor, Egypt, in 1857. Parts of the original document have been lost, but a section consisting of 14 sheets glued end to end to form a continuous roll ![]() feet wide and 17 feet long remains. Part of it is on public display in the British Museum, where it has been since 1865. Some missing pieces of this document were discovered in 1922 in the Egyptian collection of the New York Historical Society; these are now housed at the Brooklyn Museum of Art. A slightly earlier mathematical papyrus, now in the Moscow Museum of Fine Arts, consists of sheets about one-fourth the size of the Rhind papyrus. This papyrus was purchased by V. S. Golenishchev (1856–1947) in 1893 and donated to the museum in 1912. A third document, a leather roll purchased along with the Rhind papyrus, was not unrolled for 60 years after it reached the British Museum because the curators feared it would disintegrate if unrolled. It was some time before suitable techniques were invented for softening the leather, and the document was finally unrolled in 1927. The contents turned out to be a collection of 26 sums of unit fractions, from which historians were able to gain insight into Egyptian methods of calculation. A fourth set of documents, known as the Reisner papyri after the American archaeologist George Andrew Reisner (1867–1942), who purchased them in 1904, consists of four rolls of records from dockyard workshops, apparently from the reign of Senusret I (1971–1926 BCE). They are now in the Boston Museum of Fine Arts. Another document, the Akhmim Wooden Tablet, is housed in the Egyptian Museum in Cairo. The Akhmim Wooden Tablet contains several ways of expressing reciprocals of integers based on dividing unity (64/64) by these integers. According to Milo Gardner (http://mathworld.wolfram.com/AkhmimWoodenTablet.html), the significance of the number 64 is that it is the number of ro in a hekat of grain. It also relates to the so-called Horus-eye fractions, as we shall discuss below. This origin for the numbers makes sense and gives a solid practical origin for Egyptian arithmetic. These documents show the practical application of Egyptian mathematics in construction and commerce. We shall mostly discuss the Rhind papyrus in this chapter and the next, only occasionally mentioning items from the others.
feet wide and 17 feet long remains. Part of it is on public display in the British Museum, where it has been since 1865. Some missing pieces of this document were discovered in 1922 in the Egyptian collection of the New York Historical Society; these are now housed at the Brooklyn Museum of Art. A slightly earlier mathematical papyrus, now in the Moscow Museum of Fine Arts, consists of sheets about one-fourth the size of the Rhind papyrus. This papyrus was purchased by V. S. Golenishchev (1856–1947) in 1893 and donated to the museum in 1912. A third document, a leather roll purchased along with the Rhind papyrus, was not unrolled for 60 years after it reached the British Museum because the curators feared it would disintegrate if unrolled. It was some time before suitable techniques were invented for softening the leather, and the document was finally unrolled in 1927. The contents turned out to be a collection of 26 sums of unit fractions, from which historians were able to gain insight into Egyptian methods of calculation. A fourth set of documents, known as the Reisner papyri after the American archaeologist George Andrew Reisner (1867–1942), who purchased them in 1904, consists of four rolls of records from dockyard workshops, apparently from the reign of Senusret I (1971–1926 BCE). They are now in the Boston Museum of Fine Arts. Another document, the Akhmim Wooden Tablet, is housed in the Egyptian Museum in Cairo. The Akhmim Wooden Tablet contains several ways of expressing reciprocals of integers based on dividing unity (64/64) by these integers. According to Milo Gardner (http://mathworld.wolfram.com/AkhmimWoodenTablet.html), the significance of the number 64 is that it is the number of ro in a hekat of grain. It also relates to the so-called Horus-eye fractions, as we shall discuss below. This origin for the numbers makes sense and gives a solid practical origin for Egyptian arithmetic. These documents show the practical application of Egyptian mathematics in construction and commerce. We shall mostly discuss the Rhind papyrus in this chapter and the next, only occasionally mentioning items from the others.
6.2 The Rhind Papyrus
What do these documents tell us about the practice of mathematics in ancient Egypt? The author of the Rhind papyrus begins his work by describing it as a “correct method of reckoning, for grasping the meaning of things, and knowing everything that is, obscurities. . .and all secrets.”2 The author seems to value mathematics because of its explanatory power, but that explanatory power was essentially practical, not at all mystical.
We are fortunate to be able to date the Rhind papyrus with such precision. The author, a scribe named Ahmose (or Ahmes), gives us his name and tells us that he is writing in the fourth month of the flood season of the thirty-third year of the reign of Pharaoh A-user-re (Apepi I). From this information, Egyptologists arrived at a date of around 1650 BCE for this papyrus, which is approximately the latest date of the Old Babylonian cuneiform tablets discussed in the preceding chapters. Ahmose tells us, however, that he is merely copying work written down in the reign of Pharaoh Ny-maat-re, also known as Amenemhet III (1842–1797 BCE), the sixth pharaoh of the Twelfth Dynasty. From that information it follows that the mathematical knowledge contained in the papyrus is nearly 4000 years old.
The introductory paragraph of the Rhind papyrus is followed by certain tables that resemble multiplication tables (more on this subject below), along with 87 problems involving various mathematical processes. Attempts have been made to discern a pattern in the arrangement of these problems. The suggestion that seems most plausible intuitively is that the problems are grouped according to their application rather than their method of solution. The first six problems, for example, involve dividing loaves of bread among 10 people. Problems 7–23 are purely technical and show how to add fractional parts and, given a certain number of fractional parts, how to find complementary fractional parts to obtain a whole. Problems 24–38 are concerned with finding a quantity of which certain fractional parts will yield a given number. Area, volume, and general measurement problems are numbered from 40 to 60, and the remaining problems are concerned with various commercial applications to the distribution of goods.
6.3 Egyptian Arithmetic
Let us begin our discussion of Egyptian mathematics by describing the way numbers were written. In hieroglyphics, numbers are represented as vertical strokes (|) for each individual digit, up to 9; then 10 is written as ∩, 20 as ∩∩, and so on. To represent 100, the Egyptians used a symbol resembling a coil of rope. Such a system requires new symbols to be invented for higher and higher groupings, as larger and larger numbers become necessary. As Fig. 6.1shows, the Egyptians had hieroglyphic symbols for 1000 (a lotus blossom), 10,000 (a crooked thumb), 100,000 (a turbot fish), and 1,000,000 (said to be the god of the air). With this system of recording numbers, no symbol for zero was needed, nor was the order of digits of any importance, since, for example, ||| ∩ ∩ and ∩ ∩ || | both mean 23. The disadvantage of the notation is that the symbol for each power of 10 must be written a number of times equal to the digit that we would put in its place. This system is very far from our place-value decimal system, in which there are symbols for the numbers 0 through 9, interpreted as multiples of powers of ten, with the power indicated by physical location in the number. Later on, in the hieratic script that replaced hieroglyphics, they had special symbols for 1 through 9, 10 through 90, 100 through 900, and so on, as shown in Fig. 6.2. This system was later used by the Greeks, with Greek letters replacing the hieratic symbols.
Figure 6.1 Powers of 10 from 100 to 106 in hieroglyphics.

Figure 6.2 Hieratic symbols, arranged as a multiplication table.

6.4 Computation
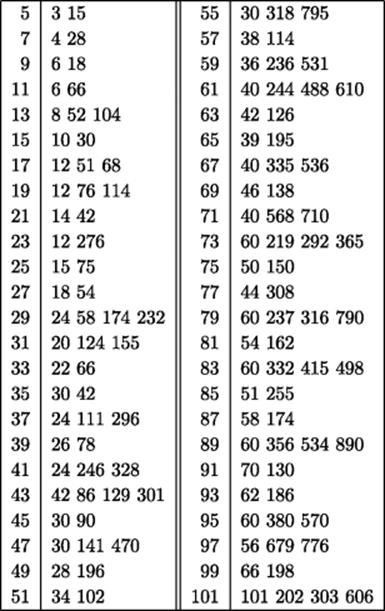
After the descriptive title, the Rhind papyrus exhibits the table of numbers shown in Fig. 6.3, which will be discussed below. In contrast to our modern arithmetic, which consists of the four operations of addition, subtraction, multiplication, and division performed on whole numbers and fractions, the fundamental operations in Egypt were addition, subtraction, and doubling, and these operations were performed on whole numbers and parts. We need to discuss both the operations and the objects on which they were carried out.
Figure 6.3 Doubles of unit fractions in the Rhind papyrus.
Let us consider first the absence of multiplication and division as we know them. First of all, there is something special about the number 2. It is a number that we can grasp easily without even having to count. It has always played a special role in ordinary conversation. For example, we don't normally say “one–twoth” for the result of dividing something in two parts. This linguistic peculiarity suggests that doubling is psychologically different from applying the general concept of multiplying in the special case when the multiplier is 2.
Next consider the absence of what we call fractions. The closest Egyptian equivalent to a fraction is something we shall call a part. For example, what we refer to nowadays as the fraction ![]() would be referred to as “the seventh part.” This way of expressing fractions has a venerable history, even in English, and you will frequently encounter it in writing from earlier centuries. The phrase “seventh part” conveys the image of a thing divided into seven equal parts arranged in a row and the seventh (and last) one being chosen. For that reason, according to van der Waerden (1963), there can be only one seventh part, namely the last one; there would be no way of expressing what we call the fraction
would be referred to as “the seventh part.” This way of expressing fractions has a venerable history, even in English, and you will frequently encounter it in writing from earlier centuries. The phrase “seventh part” conveys the image of a thing divided into seven equal parts arranged in a row and the seventh (and last) one being chosen. For that reason, according to van der Waerden (1963), there can be only one seventh part, namely the last one; there would be no way of expressing what we call the fraction ![]() , since there couldn't be three seventh parts. An exception was the fraction that we call
, since there couldn't be three seventh parts. An exception was the fraction that we call ![]() , which occurs constantly in the Rhind papyrus. There was a special symbol meaning “the two parts” out of three. It is very easy to interpret parts in our own language. They are unit fractions, that is, fractions whose numerator is 1. But for historical purposes, it is better to retain the obsolete language of parts. Our familiarity with fractions in general makes it difficult to see what the fuss is about when the author asks what must be added to the two parts and the fifteenth part in order to make a whole (Problem 21 of the papyrus). If this problem is stated in modern notation, it merely asks for the value of
, which occurs constantly in the Rhind papyrus. There was a special symbol meaning “the two parts” out of three. It is very easy to interpret parts in our own language. They are unit fractions, that is, fractions whose numerator is 1. But for historical purposes, it is better to retain the obsolete language of parts. Our familiarity with fractions in general makes it difficult to see what the fuss is about when the author asks what must be added to the two parts and the fifteenth part in order to make a whole (Problem 21 of the papyrus). If this problem is stated in modern notation, it merely asks for the value of ![]() . We get the answer immediately, expressing it as
. We get the answer immediately, expressing it as ![]() . Both this process and the answer would have been foreign to the Egyptian, whose solution is described below.
. Both this process and the answer would have been foreign to the Egyptian, whose solution is described below.
To understand the Egyptians, we shall try to imitate their way of writing down a problem. On the other hand, we would be at a great disadvantage if our desire for authenticity led us to try to solve the entire problem using their notation. The best compromise seems to be to use our symbols for the whole numbers and express a part by the corresponding whole number with a bar over it. Thus, the fifth part will be written ![]() , the thirteenth part will be represented by
, the thirteenth part will be represented by ![]() , and so on. For “the two parts”
, and so on. For “the two parts” ![]() we shall use a double bar, that is,
we shall use a double bar, that is, ![]() .
.
6.4.1 Multiplication and Division
Since the only operation other than addition and subtraction of integers (which are performed automatically without comment) is doubling, the problem that we would describe as “multiplying 11 by 19” would have been written out as follows:

Inspection of this process shows its justification. The rows are kept strictly in proportion by doubling each time. The final result can be stated by comparing the first and last rows: 19 is to 1 as 209 is to 11. The rows in the right-hand column that must be added in order to obtain 11 are marked with an asterisk, and the corresponding entries in the left-hand column are then added to obtain 209. In this way any two positive integers can easily be multiplied. The only problem that arises is to decide how many rows to write down and which rows to mark with an asterisk. But that problem is easily solved. You stop creating rows when the next entry in the right-hand column would be bigger than the number you are multiplying by (in this case 11). You then mark your last row with an asterisk, subtract the entry in its right-hand column (8) from 11 (getting a remainder of 3), then move up and mark the next row whose right-hand column contains an entry not larger than this remainder (in this case the second row), subtract the entry in its right-hand column (2), from the previous remainder to get a smaller remainder (in this case 1), and so forth.
We shall refer to this general process of doubling and adding as calculating. What we call division is carried out in the same way, by reversing the roles of the two columns. For example, what we would call the problem of dividing 873 by 97 amounts to calculating with 97 so as to obtain 873. We can write it out as follows:
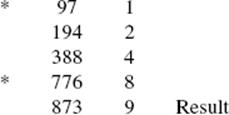
The process, including the rules for creating the rows and deciding which ones to mark with an asterisk, is exactly the same as in the case of multiplication, except that now it is the left-hand column that is used rather than the right-hand column. We create rows until the next entry in the left-hand column would be larger than 873. We then mark the last row, subtract the entry in its left-hand column from 873 to obtain the remainder of 97, then look for the next row above whose left-hand entry contains a number not larger than 97, mark that row, and so on.
6.4.2 “Parts”
It has probably occurred to you that the second use of the two-column system may lead to complications. While in the first problem we can always express any positive integer as a sum of powers of 2, the second problem is a different matter. We were just lucky that we happened to find multiples of 97 that add up to 873. If we hadn't found them, we would have had to deal with those parts that have already been discussed. For example, if the problem were “calculate with 12 so as to obtain 28,” it might have been handled as follows:

What is happening in this computation is the following. We stop creating rows after 24 because the next entry in the left-hand column (48) would be bigger than 28. Subtracting 24 from 28, we find that we still need 4, yet no 4 is to be found. We therefore go back to the first row and multiply by ![]() , getting the row containing 8 and
, getting the row containing 8 and ![]() . Dividing by 2 again gets a 4 in the left-hand column. We then have the numbers we need to get 28, and the answer is expressed as 2
. Dividing by 2 again gets a 4 in the left-hand column. We then have the numbers we need to get 28, and the answer is expressed as 2 ![]() . Quite often the first multiplication by a part involves the two-thirds part
. Quite often the first multiplication by a part involves the two-thirds part ![]() . The scribes probably began with this part instead of one-half for the same reason that a carpenter uses a plane before sandpaper: The work goes faster if you take bigger “bites.”
. The scribes probably began with this part instead of one-half for the same reason that a carpenter uses a plane before sandpaper: The work goes faster if you take bigger “bites.”
The parts that are negative powers of 2 play a special role. When applied to a hekat of grain, they are referred to as the Horus-eye parts. According to Egyptian legend, the god Horus lost an eye in a fight with his uncle, and the eye was restored by the god Thoth. Each of these fractions was associated with a particular part of Horus' eye. Since 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 = 63/64, the scribes apparently saw that unity could be restored (approximately), as Horus' eye was restored, by using these parts. The fact that (in our terms) 63 occurs as a numerator shows that division by 3, 7, and 9 is facilitated by the use of the Horus-eye series. In particular, since 1/7 = (1/7) · ((63/64) + 1/64) = 9/64 + 1/448 = 8/64 + 1/64 + 1/448, the seventh part could have been written as ![]()
![]()
![]() . In this way, the awkward seventh part gets replaced by the better-behaved Horus-eye fractions, plus a corrective term (in this case
. In this way, the awkward seventh part gets replaced by the better-behaved Horus-eye fractions, plus a corrective term (in this case ![]() , which might well be negligible in practice). Five such replacements are implied, though not given in detail, in the Akhmim Wooden Tablet. As another example, since 64 = 4 · 13 + 8 + 4, which, when both expressions are divided by 13 × 64, becomes
, which might well be negligible in practice). Five such replacements are implied, though not given in detail, in the Akhmim Wooden Tablet. As another example, since 64 = 4 · 13 + 8 + 4, which, when both expressions are divided by 13 × 64, becomes ![]() , we find that
, we find that ![]() =
= ![]()
![]()
![]() . This expansion makes it easy to see how to write the double of
. This expansion makes it easy to see how to write the double of ![]() in terms of parts.
in terms of parts.
There are two more complications that arise in doing arithmetic the Egyptian way. The first complication is obvious. Since the procedure is based on doubling, but the double of a part may not be expressible as a part, how does one “calculate” with parts? It is easy to double, say, the twenty-sixth part: The double of the twenty-sixth part is the thirteenth part. If we try to double again, however, we are faced with the problem of doubling a part involving an odd number. The table at the beginning of the papyrus gives the answer: The double of the thirteenth part is the eighth part plus the fifty-second part plus the one hundred fourth part. In our terms this tabular entry expresses the fact that
![]()
Gillings (1972, p. 49) lists five precepts apparently followed by the compiler of this table in order to make it maximally efficient for use. The most important of these are the following three. One would like each double (1) to have as few terms as possible, (2) with each term as small as possible (that is, the “denominators” as small as possible), and (3) with even “denominators” rather than odd ones. These principles have to be balanced against one another, and the table in Fig. 6.3 represents the resulting compromise. However, Gillings' principles are purely negative ones, telling what not to do. The positive side of creating such a table is to find simple patterns in the numbers. One pattern that occurs frequently is illustrated by the double of ![]() , and amounts to the identity 2/p = 1/((p + 1)/2) + 1/(p(p + 1)/2). Another, illustrated by the double of
, and amounts to the identity 2/p = 1/((p + 1)/2) + 1/(p(p + 1)/2). Another, illustrated by the double of ![]() , probably arises from the Horus-eye representation of the original part.
, probably arises from the Horus-eye representation of the original part.
With this table, which gives the doubles of all parts involving an odd number up to 101, calculations involving parts become feasible. There remains, however, one final complication before one can set out to solve problems. The calculation process described above requires subtraction at each stage in order to find what is lacking in a given column. When the column already contains parts, this leads to the second complication: the problem of subtracting parts. (Adding parts is no problem. The author merely writes them one after another. The sum is condensed if, for example, the author knows that the sum of ![]() and
and ![]() is
is ![]() .) This technique, which is harder than the simple procedures discussed above, is explained in the papyrus itself in Problems 21–23. As mentioned above, Problem 21 asks for the parts that must be added to the sum of
.) This technique, which is harder than the simple procedures discussed above, is explained in the papyrus itself in Problems 21–23. As mentioned above, Problem 21 asks for the parts that must be added to the sum of ![]() and
and ![]() to obtain 1. The procedure used to solve this problem is as follows. Begin with the two parts in the first row:
to obtain 1. The procedure used to solve this problem is as follows. Begin with the two parts in the first row:
![]()
Now the problem is to see what must be added to the two terms on the left-hand side in order to obtain the right-hand side. Preserving proportions, the author multiplies the row by 15, getting
![]()
It is now clear that when the problem is “magnified” by a factor of 15, we need to add 4 units. Therefore, the only remaining problem is, as we would put it, to divide 4 by 15, or in language that may reflect better the thought process of the author, to “calculate with 15 so as to obtain 4.” This operation is carried out in the usual way:
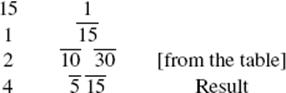
Thus, the parts that must be added to the sum of ![]() and
and ![]() in order to reach 1 are
in order to reach 1 are ![]() and
and ![]() . This “subroutine,” which is essential to make the system of computation work, was written in red ink in the manuscripts, as if the writers distinguished between computations made within the problem to find the answer and computations made in order to operate the system. Having learned how to complement (subtract) parts, what are called hau (or aha) computations by the author, one can confidently attack any arithmetic problem whatsoever. Although there is no single way of doing these problems, specialists in this area have detected (a) systematic procedures by which the table of doubles was generated and (b) patterns in the solution of problems that indicate, if not an algorithmic procedure, at least a certain habitual approach to such problems.
. This “subroutine,” which is essential to make the system of computation work, was written in red ink in the manuscripts, as if the writers distinguished between computations made within the problem to find the answer and computations made in order to operate the system. Having learned how to complement (subtract) parts, what are called hau (or aha) computations by the author, one can confidently attack any arithmetic problem whatsoever. Although there is no single way of doing these problems, specialists in this area have detected (a) systematic procedures by which the table of doubles was generated and (b) patterns in the solution of problems that indicate, if not an algorithmic procedure, at least a certain habitual approach to such problems.
Let us now consider how these principles are used to solve a problem from the papyrus. The one we pick is Problem 35, which, translated literally and misleadingly, reads as follows: Go down 1 times 3. My third part is added to me. It is filled. What is the quantity saying this? To clarify: This problem asks for a number that yields 1 when it is tripled and the result is then increased by the third part of the original number. In other words, “calculate with 3 ![]() so as to obtain 1.” The solution is as follows:
so as to obtain 1.” The solution is as follows:
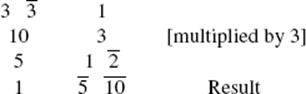
Problems and Questions
Mathematical Problems
6.1 Double the hieroglyphic number ![]() .
.
6.2 Multiply 27 times 42 the Egyptian way.
6.3 (Stated in the Egyptian style.) Calculate with 13 so as to obtain 364.
Historical Questions
6.4 What are the main documentary sources for our knowledge of ancient Egyptian mathematics?
6.5 What benefits are to be gained from learning mathematics, according to the author of the Rhind papyrus?
6.6 Is the information in the Rhind papyrus older or more recent than what is found on the Old Babylonian tablets?
Questions for Reflection
6.7 Why do you suppose that the author of the Rhind papyrus did not choose to say that the double of the thirteenth part is the seventh part plus the ninety-first part, that is,
![]()
Why is the relation
![]()
made the basis for the tabular entry instead?
6.8 How do you account for the fact that the ancient Greeks used a system of counting and calculating that mirrored the notation found in Egypt, whereas in their astronomical measurements they borrowed the sexagesimal system of Mesopotamia? Why were they apparently blind to the computational advantages of the place-value system used in Mesopotamia?
6.9 Could the ability to solve a problem such as Problem 35 of the Rhind papyrus, discussed above, have been of any practical use? Try to think of a situation in which such a problem might arise.
Notes
1. Analogous to the Stephanus indexing of the works of Plato, which will be mentioned in Section 8.2 of Chapter 8, the works of Aristotle were issued by the Prussian Academy of Sciences in the nineteenth century, edited by August Immanuel Bekker (1785–1871).
2. This is the translation given by Robins and Shute (1987, p. 11). Chace et al. (1927, p. 49) give the translation as “the entrance into the knowledge of all existing things and all secrets.”