The history of mathematics: A brief course (2013)
Part III. Greek Mathematics From 500 BCE to 500 CE
During the millennium from 500 BCE to 500 CE, mathematics, especially geometry, was imported into Greece, became mixed with the speculations of the Greek philosophers and developed into a body of knowledge that was unique in its time. The center of gravity gradually shifted from the commercial Ionian colonies in the early period (along with their colonies in Italy and Sicily) to Athens in the fifth century, reaching its peak in the third century at Alexandria, Egypt. Along with this new, formal geometry, some of the earlier, more practically oriented geometry survived and revived after the time of the three greatest geometers of antiquity (Euclid, Archimedes, and Apollonius). This practical geometry was applied to produce one great astronomical treatise, the Almagest of Claudius Ptolemy, which became a standard reference for the next thousand years. After Ptolemy, the potential of the Euclidean methods was nearly exhausted, and there is little that is original in the last few centuries we are going to discuss. The one exception comes from number theory, rather than geometry, and it is the invention of symbolic algebraic notation by Diophantus in order to solve problems involving the arithmetic properties of figurate numbers. The next 11 chapters give a sketch of some of the highlights of this long period of development.
Contents of Part III
1. Chapter 8 (An Overview of Ancient Greek Mathematics) gives a survey of the whole period and summarizes the sources on which our knowledge of it is based.
2. Chapter 9 (Greek Number Theory) looks at ancient Greek number theory through the works of Euclid, Nicomachus, and Diophantus.
3. Chapter 10 (Fifth-Century Greek Geometry) presents a hypothetical scenario for the development of geometry up to the mid-fifth century BCE.
4. Chapter 11 (Athenian Mathematics I: The Classical Problems) brings the development of geometry in Athens to the end of the fourth century BCE.
5. Chapter 12 (Athenian Mathematics II: Plato and Aristotle) discusses the connection of this geometry with the philosophies of Plato and Aristotle.
6. Chapter 13 (Euclid of Alexandria) analyzes the Elements and looks briefly at some other works by Euclid.
7. Chapter 14 (Archimedes of Syracuse) is devoted to the works of Archimedes.
8. Chapter 15 (Apollonius of Perga) discusses the extensive treatise on conic sections by Apollonius of Perga.
9. Chapter 16 (Hellenistic and Roman Geometry) discusses the isoperimetric problems studied by Zenodorus and the return of metric concepts to geometry in the work of Heron of Alexandria.
10. Chapter 17 (Ptolemy's Geography and Astronomy) is devoted to the geographical and astronomical treatises of Claudius Ptolemy.
11. Chapter 18 (Pappus and the Later Commentators) summarizes the work of the later commentators Pappus, Theon of Alexandria, and Theon's daughter Hypatia.
Chapter 8. An Overview of Ancient Greek Mathematics
Greek was the common language of scholarship in the region around the Mediterranean for at least nine hundred years, from the time of the Athenian Empire in the mid-fifth century BCE until the Western half of the Roman Empire was destroyed by invaders from the north in the late fifth century CE, after which contacts between the Western Latin-based portion and the Eastern Greek-speaking portion began to decline. The Roman Empire was multinational, and not all those who contributed to this scholarship were native speakers of Greek. Although the great classic works of the third century BCE probably were written by native Greek speakers—Archimedes certainly was one—some of the later commentators may have had other roots. What we call ancient Greek mathematics is therefore mathematics originally written in Greek, not necessarily by Greeks, and some of it survives only in Arabic translation.
The origin, flourishing, and decline of ancient Greek mathematics took place over a period approximately 1000 years in extent, beginning with the philosopher Thales (ca. 624–546) and ending with the death of Hypatia in 415 CE. It arose during the Hellenic era from 600 to 300 BCE, when the Greek city–states were independent, achieved its greatest heights during the Hellenistic period after the conquests of Alexander the Great, and underwent stagnation and decline after the rise of the Roman Empire, while still producing some remarkable works during its final 500 years.
The Greeks of the Hellenic period traced the origins of their mathematical knowledge to Egypt and the Middle East. This knowledge probably came in “applied” form in connection with commerce and astronomy/astrology. Mesopotamian numerical methods appear in the later Hellenistic work on astronomy by Hipparchus (second century BCE) and the work of Ptolemy under the Roman Empire. Earlier astronomical models by Eudoxus (fourth century BCE) and Apollonius (third century BCE) were more geometrical. Jones (1991, p. 445) notes that “the astronomy that the Hellenistic Greeks received from the hands of the Babylonians was by then more a skill than a science: The quality of the predictions was proverbial, but in all likelihood the practitioners knew little or nothing of the origins of their schemes in theory and observations.” Among the techniques transmitted to the Greeks and ultimately to the modern world was the convention of dividing a circle into 360 equal parts (degrees). Greek astronomers divided the radius into 60 equal parts so that the units of length on the radius and on the circle were very nearly equal.
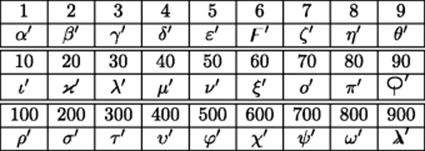
The amount that the Greeks learned from Egypt is the subject of controversy. Some scholars who have read the surviving mathematical texts from papyri have concluded that Egyptian methods of computing were too cumbersome for application to the complicated measurements of astronomers. Yet both Plato and Aristotle speak approvingly of Egyptian computational methods and the ways in which they were taught. As for geometry, it is generally acknowledged that the Egyptian insight was extraordinary; the Egyptians knew how to find the volume of a frustum of a pyramid, and it appears that they even found the area of a hemisphere, the only case known before Archimedes in which the area of a curved surface is found.1 The case for advanced Egyptian mathematics is argued by Bernal (1992), who asserts that Ptolemy himself was an Egyptian. The question is difficult to settle, since little is known of Ptolemy personally; for us, he is simply the author of certain works on physics, astronomy, and geography. One particular aspect of Greek mathematics, however, does bear a strong resemblance to that of Egypt, namely their system of writing numbers. It is shown here in Fig. 8.1, which is to be compared with Fig. 6.2 of Chapter 6.
Figure 8.1 The ancient Greek numbering system.
Because of their extensive commerce, with its need for counting, measurement, navigation, and an accurate calendar, the Ionian Greek colonies such as Miletus on the coast of Asia Minor and Samos in the Aegean Sea provided a very favorable environment for the development of mathematics, and it was there, with the philosophers Thales of Miletus and Pythagoras of Samos (ca. 570–475 BCE), that Greek mathematics began.
8.1 Sources
Since the material on which the Greeks wrote was not durable, all the original manuscripts have been lost except for a few ostraca (shells) found in Egypt. We are dependent on copyists for preserving the information in early Greek works, since few manuscripts that still exist were written more than 1000 years ago. We are further indebted to the many commentators who wrote summary histories of philosophy, including mathematics, for the little that we know about the works that have not been preserved and their authors. The most prominent among these commentators are listed below. They will be mentioned many times in the chapters that follow.
1. Marcus Vitruvius (first century BCE) was a Roman architect who wrote a treatise on architecture in 10 books. He is regarded as a rather unreliable source for information about mathematics, however.
2. Plutarch (45–120 CE) was a pagan author, apparently one of the best educated people of his time, who wrote on many subjects. He is best remembered as the author of the Parallel Lives of the Greeks and Romans, in which he compares famous Greeks with eminent Romans who engaged in the same occupation, such as the orators Demosthenes and Cicero.2 Plutarch is important to the history of mathematics for what he reports on natural philosophers such as Thales.
3. Theon of Smyrna (ca. 100 CE) was the author of an introduction to mathematics written as background for reading Plato, a copy of which still exists. It contains many quotations from earlier authors.
4. Diogenes Laertius (third century CE) wrote a comprehensive history of philosophy, Lives of Eminent Philosophers, which contains summaries of many earlier works and gives details of the lives and work of many of the pre-Socratic philosophers. He appears to be the source of the misnomer “Pythagorean theorem” that has come down to us (see Zhmud, 1989, p. 257).
5. Iamblichus (285–330 CE) was the author of many treatises, including 10 books on the Pythagoreans, five of which have been preserved.
6. Pappus (ca. 300 CE) wrote many books on geometry, including a comprehensive treatise of eight mathematical books. He is immortalized in calculus books for his theorem on the volume of a solid of revolution. Besides being a first-rate geometer in his own right, he wrote commentaries on the Almagest of Ptolemy and the tenth book of Euclid's Elements.
7. Theon of Alexandria (late fourth century CE), a commentator and philosopher who is probably responsible for the now-standard Greek edition of Euclid's Elements.
8. Hypatia of Alexandria (ca. 370–415), a neo-Platonist philosopher, daughter of Theon of Alexandria. She may be the editor of the Greek text of Diophantus' Arithmetica.
9. Proclus (412–485 CE) is the author of a commentary on the first book of Euclid, in which he seems to have quoted a long passage from a history of mathematics, now lost, by Eudemus, a pupil of Aristotle.
10. Simplicius (500–549 CE) was a commentator on philosophy. His works contain many quotations from the pre-Socratic philosophers.
11. Eutocius (ca. 700 CE) was a mathematician who lived in the port city of Askelon in Palestine and wrote an extensive commentary on the works of Archimedes.
8.1.1 Loss and Recovery
Most of these commentators wrote in Greek. Knowledge of Greek sank to a very low level in western Europe as a result of the upheavals of the fifth century. Although learning was preserved by the Catholic Church and all of the New Testament was written in Greek, a Latin translation (the Vulgate) was made by Jerome in the fifth century. From that time on, Greek documents were preserved mostly in the Eastern (Byzantine) Empire. After the Muslim conquest of North Africa and Spain in the eighth century, some Greek documents were translated into Arabic and circulated in Spain and the Middle East. From the eleventh century on, as secular learning began to revive in the West, scholars from northern Europe made journeys to these centers and to Constantinople, copied out manuscripts, translated them from Arabic and Greek into Latin, and tried to piece together some long-forgotten parts of ancient learning.
8.2 General Features of Greek Mathematics
Greek mathematics—that is, mathematics written in ancient Greek—is exceedingly rich in authors and works. Its most unusual feature, compared with what went before, is its formal development. From the time of Euclid on, mathematics was developed systematically from definitions and axioms, general theorems were stated, and proofs were given. This formal development is the outcome of the entanglement of mathematics with Greek philosophy. It became a model to be imitated in many later scientific treatises, such as Newton's Philosophiæ naturalis principia mathematica. Principia, Of course, Greek mathematics did not arise in the finished form found in the treatises. Tradition credits Thales, the earliest Greek philosopher, with knowing four geometric propositions. Thales was said to have traveled to Egypt and determined the height of the Great Pyramid of Khufu using similar triangles. One of the four geometric propositions that Thales is said to have known is that an angle inscribed in a semicircle is a right angle.3
Herodotus mentions Thales in several places. Discussing the war between the Medes and the Lydian king Croesus, which had taken place in the previous century, he says that an eclipse of the sun frightened the combatants into making peace. Thales, according to Herodotus, had predicted that an eclipse would occur no later than the year in which it actually occurred. Herodotus goes on to say that Thales had helped Croesus to divert the river Halys so that his army could cross it.
These anecdotes show that Thales had both scientific and practical interests. His prediction of a solar eclipse, which, according to the astronomers, occurred in 585 BCE, seems quite remarkable, even if, as Herodotus says, he gave only a period of several years in which the eclipse was to occur. Although solar eclipses occur regularly, they are visible only over small portions of the earth, so that their regularity is difficult to discover and verify. Lunar eclipses exhibit the same period as solar eclipses and are easier to observe. Eclipses recur in cycles of about 19 solar years, a period that seems to have been known to many ancient peoples. Among the cuneiform tablets from Mesopotamia, there are many that discuss astronomy, and Ptolemy uses Mesopotamian observations in his system of astronomy. Thales could have acquired this knowledge, along with certain simple facts about geometry, such as the fact that the base angles of an isosceles triangle are equal. Bychkov (2001) argues that the recognition that the base angles of an isosceles triangle are equal probably did come from Egypt. In construction—for example, putting a roof on a house—it is not crucial that the cross section be exactly an isosceles triangle, since it is the horizontal edge of the roof that must fit precisely, not the two slanting edges. But when a symmetric square pyramid is built, errors in the base angles of the faces would make it impossible for the faces to fit together tightly along the four oblique edges. Therefore, he believes, Thales must have derived this theorem from his travels in Egypt.
The history of Greek geometry up to the time of Euclid (300 BCE) was written by Eudemus, a pupil of Aristotle. This history was lost, but it is believed to be the basis of the first paragraph of a survey given by Proclus in the fifth century CE in the course of his commentary on the first book of Euclid. In this passage, Proclus mentions 25 men who were considered to have made significant contributions to mathematics. Of these 25, five are well known as philosophers (Thales, Pythagoras, Anaxagoras, Plato, and Aristotle); three are famous primarily as mathematicians and astronomers (Euclid, Eratosthenes, and Archimedes). The other 17 have enjoyed much less posthumous fame. Some of them are so obscure that no mention of them can be found anywhere except in Proclus' summary. Some others (Theodorus, Archytas, Menaechmus, Theaetetus, and Eudoxus) are mentioned by other commentators or by Plato. The 13 just named are the main figures we shall use to sketch the history of Greek geometry. It is clear from what Proclus writes that something important happened to mathematics during the century of Plato and Aristotle, and the result was a unique book, Euclid's Elements.
Missing from the survey of Proclus is any reference to Mesopotamian influence on Greek geometry. This influence is shown clearly in Greek astronomy, in the use of the sexagesimal system of measuring angles and in Ptolemy's explicit use of Mesopotamian astronomical observations. It may also appear in Book 2 of Euclid's Elements, which contains geometric constructions equivalent to certain algebraic relations that are frequently encountered in the cuneiform tablets. This relation, however, is controversial. Leaving aside the question of Mesopotamian influence, we do see a recognition of the Greek debt to Egypt. (Recall Herodotus' conjecture on the origin of Greek geometry from Chapter 7. Euclid actually lived in Egypt, and the other two of the “big three” Greek geometers, Archimedes and Apollonius, both studied there, in the Hellenistic city of Alexandria at the mouth of the Nile.)
8.2.1 Pythagoras
By the time of Pythagoras, geometric lore had expanded beyond the propositions ascribed to Thales, and later commentators constructed an elaborate scenario of a Pythagorean school that devoted itself to the contemplation of geometry and number theory. Although there certainly was a school of Pythagoreans, and Pythagoras was a real person, recent scholarship has cast doubt on its connection with mathematics. In particular, a close analysis of the best-attested citations of Pythagorean doctrine by Burkert (1962) yields a picture of a school preoccupied with mysticism and personal discipline, but not necessarily mathematics. Nevertheless, there remain numerous attributions of mathematical results to the Pythagoreans in the works of the later commentators. Is it possible that Burkert's observation is actually a matter of selection bias on the part of the people who made the quotations? Perhaps these quotations from Pythagoras were chosen by people for whom mathematics was not a priority. It is not certain that all the other attributions of mathematical results to the Pythagoreans are spurious. Even if we grant the possibility that the geometers who assembled the systematic knowledge ascribed to the Pythagoreans actually worked in Athens, perhaps in Plato's Academy during the early fourth century BCE, after the demise of the original group of Pythagoreans and that these attributions are legends not corresponding to fact, the mere existence of so many attributions makes the name Pythagorean mathematics useful as a general description of this pre-Euclidean mathematics.
The philosopher Pythagoras was born on the island of Samos, another of the Greek colonies in Ionia, about half a century after Thales. No books of Pythagoras survive, but many later writers mention him, including Aristotle. Diogenes Laertius devotes a full chapter to the life of Pythagoras. He acquired even more legends than Thales. According to Diogenes Laertius, who cites the grammarian Apollodorus of Athens (ca. 180–ca. 120), Pythagoras sacrificed 100 oxen when he discovered the theorem that now bears his name. If the stories about Pythagoras can be believed, he, like Thales, traveled widely, to Egypt and Mesopotamia. He gathered about him a large school of followers, who observed a mystical discipline and devoted themselves to contemplation. They lived in at least two places in Italy, first at Croton, then, after being driven out,4 at Metapontion, where he died in the early fifth century BCE.
According to Book I, Chapter 9 of Attic Nights, by the Roman writer Aulus Gellius (ca. 130–180), the Pythagoreans first looked over potential recruits for physical signs of being educable. Those they accepted were first classified as akoustikoí (auditors) and were compelled to listen without speaking. After making sufficient progress, they were promoted to math
matikoí (learners).5 Finally, after passing through that state they became physikoí (natural philosophers). In his book On the Pythagorean Life, Iamblichus uses these terms to denote the successors of Pythagoras, who split into two groups, the akoustikoí and the mathmatikoí. According to Iamblichus, the mathmatikoírecognized the akoustikoí as genuine Pythagoreans, but the sentiment was not reciprocated. The akoustikoí kept the pure Pythagorean doctrine and regarded the mathmatikoí as followers of a disgraced former Pythagorean named Hippasus. This part of the legend probably arose from a passage in Chapter 18, Section 88 of On the Pythagorean Life, in which Iamblichus says that Hippasus perished at sea, a punishment for his impiety because he published “the sphere of the 12 pentagons” (probably the radius of the sphere circumscribed about a dodecahedron), taking credit as if he had discovered it, when actually everything was a discovery of That Man (Pythagoras, who was too august a personage to be called by name). Apparently, new knowledge was to be kept in-house as a secret of the initiated and attributed in a mystical sense to Pythagoras.
Diogenes Laertius quotes the philosopher Alexander Polyhistor (ca. 105–35 BCE) as saying that the Pythagoreans generated the world from monads (units). By adding a single monad to itself, they generated the natural numbers. By allowing the monad to move, they generated a line, then by further motion the line generated plane figures (polygons), and the plane figures then moved to generate solids (polyhedra). From the regular polyhedra they generated the four elements of earth, air, fire, and water.
From all these sources, one can see how a consistent picture arose of Pythagoreans devoted to understanding the universe mathematically. Despite this plethora of independent sources from ancient times, this picture is not quite consistent with other documents from the schools of Plato and Aristotle, which indicate that the original Pythagorean group disappeared not long after the death of Pythagoras himself. For that reason, we shall use the word Pythagorean sparingly. But we shall use it, since so many ancient authors accepted this view of the history of the subject and wrote as if it were true.
From Proclus and other later authors we have a picture of a sophisticated Pythagorean geometry, entwined with mysticism. For example, Proclus reports that the Pythagoreans regarded the right angle as ethically and aesthetically superior to acute and obtuse angles, since it was “upright, uninclined to evil, and inflexible.” Right angles, he says, were referred to the “immaculate essences,” while the obtuse and acute angles were assigned to divinities responsible for changes in things. The Pythagoreans had a bias in favor of the eternal over the changeable, and they placed the right angle among the eternal things, since unlike acute and obtuse angles, it cannot change without losing its character. In taking this view, Proclus is being a strict Platonist, because Plato's ideal forms were defined precisely by their absoluteness; they were incapable of undergoing any change without losing their identity.
8.2.2 Mathematical Aspects of Plato's Philosophy
Plato was interested in mathematics for both philosophical and political reasons. He wanted to solve the crucial problem of governing a state and keeping it stable. To that end, he knew that those with political power needed to understand natural science, and he hoped to provide a “theory of everything,” based on fundamental concepts perceived by the mind, that could be understood by every educated person. Plato is famous for his theory of ideas, which had both metaphysical and epistemological aspects. The metaphysical aspect was a response to two of his predecessors, Heraclitus of Ephesus (ca. 535–475 BCE), who asserted that everything is in constant flux, and Parmenides (born around 515 BCE), who asserted that knowledge is possible only in regard to things that do not change. One can see the obvious implication: Everything changes (Heraclitus). Knowledge is possible only about things that do not change (Parmenides). Therefore. . . . To avoid the implication that no knowledge is possible, Plato restricted the meaning of Heraclitus' “everything” to objects of sense and invented eternal, unchanging forms (ideas) that could be objects of knowledge.
The epistemological aspect of Plato's philosophy involves universal propositions, statements such as “Lions are carnivorous” (our example, not Plato's), meaning “All lions are carnivorous.” This sentence is grammatically (syntactically) inconsistent with its meaning (semantics). The grammatical subject is the set of all lions, while the assertion is not about this set but about each of its individual members. It asserts that each of them is a carnivore, and therein lies the epistemological problem. What is the real semantic subject of this sentence, as opposed to the syntactical subject, which is the phrase All lions? It is not any particular lion. Plato tried to solve this problem by inventing the form or idea of a lion. He would have said that the sentence really asserts a relation perceived in the mind between the form of a lion and the form of a carnivore. Mathematics, because it dealt with objects and relations perceived by the mind, appeared to Plato to be the bridge between the world of sense and the world of forms. Nevertheless, mathematical objects were not the same thing as the forms. Each form, Plato claimed, was unique. Otherwise, the interpretation of universal propositions by use of forms would be ambiguous. But mathematical objects such as lines are not unique. There must be at least three lines, for example, in order for a triangle to exist. Hence, as a sort of hybrid of sense experience and pure mental creation, mathematical objects offered a way for the human soul to ascend to the height of understanding, by perceiving the forms themselves. Incorporating mathematics into education so as to realize this program was Plato's goal, and his pupils studied mathematics in order to achieve it. Although the philosophical goal was not reached, the effort expended on mathematics was not wasted; certain geometric problems were solved by people associated with Plato, providing the foundation of Euclid's famous work, known as the Elements.
A little over half a century after Plato's death, Euclid wrote his famous treatise, the Elements, which is quite free of all the metaphysical distractions that had preoccupied Plato. Later, neo-Platonic philosophers such as Proclus attempted to reintroduce philosophical ideas into their commentary on Euclid's work. Neugebauer (1975, p. 572) described the philosophical aspects of Proclus' introduction as “gibberish,” and expressed relief that scientific methodology survived despite the prevalent dogmatic philosophy.
According to Diels (1951, 44A5), Plato met the Pythagorean Philolaus in Sicily in 390. In any case, Plato must certainly have known the work of Philolaus, since in the Phaedo, Socrates says that both Cebes and Simmias are familiar with the work of Philolaus and implies that he himself knows of it at second hand. It seems likely, then, that Plato's interest in mathematics began some time after the death of Socrates and continued for the rest of his life, that mathematics played an important role in the curriculum of his Academy and the research conducted there, and that Plato himself played a role in directing that research. We do not, however, have any theorems that can with confidence be attributed to Plato himself. Lasserre (1964, p. 17) believed that the most important mathematical work at the Academy was done between 375 and 350 BCE.
In Book VII of Plato's Republic, Socrates explained that arithmetic was needed both to serve the eye of the soul and as a practical instrument in planning civic projects and military campaigns:
The kind of knowledge we are seeking seems to be as follows. It is necessary for a military officer to learn (matheîn) these things for the purpose of proper troop deployment, and the philosopher must have risen above change, in order to grasp the essence of things, or else never become skilled in calculation (logistikós).
Later in the same book, Plato, through Socrates, complains of the lack of a government subsidy for geometry. In his day, solid geometry was underdeveloped in comparison with plane geometry, and Socrates gave what he thought were the reasons for its backwardness:
First, no government holds [the unsolved problems in solid geometry] in honor; and they are researched in a desultory way, being difficult. Second, those who are doing the research need a mentor, without which they will never discover anything. But in the first place, to become a mentor is difficult; and in the second place, after one became a mentor, as things are just now, the arrogant people doing this research would never listen to him. But if the entire state were to act in concert in conducting this research with respect, the researchers would pay heed, and by their combined intensive work the answers would become clear.
Plato himself, although he had practical objects in mind, connected with the best possible government, was also an intellectual for whom the “eye of the soul” was sufficient justification for intellectual activity. He seems to have had a rather dim view of purely practical-minded people. In his long dialogue The Laws, one of the speakers, an Athenian, rants about the shameful Greek ignorance of incommensurables, surely a topic of limited application in the lives of most people. (Plato would probably say even worse things about the modern world, where almost no one knows what incommensurables are!)
8.3 Works and Authors
Extensive treatises on mathematics written in Greek began appearing early in the Hellenistic era (third century BCE) and continued in a steady stream for hundreds of years. We list here only a few of the most outstanding authors.
8.3.1 Euclid
This author lived and worked in Alexandria, having been invited by Ptolemy Soter (Ptolemy I) shortly after the city was founded. At the 2006 winter meeting of the Canadian Mathematical Society, historian Alexander Jones argued that Euclid probably flourished around the middle of the third century and was a contemporary of Archimedes. Essentially nothing is known of his life beyond the fact that he worked in Alexandria, but his famous treatise on the basics of geometry (the Elements) has become a classic known all over the world. Several of his minor works—the Optics, the Data, and the Phænomena—also have been preserved. Euclid did not provide any preface to tell us why he wrote his treatise. We do, however, know enough of the Platonic philosophy to understand why he developed geometry and number theory to the extent that he did, and it is safe to conclude that this kind of work was considered valuable because it appealed to the intellect of those who could understand it.
8.3.2 Archimedes
Much more is known of Archimedes (ca. 287–212 BCE). About 10 of his works have been preserved, including the prefaces that he wrote in the form of “cover letters” to the people who received the works. Here is one such letter, which accompanied a report of what may well be regarded as his most profound achievement—proving that the surface of a sphere is four times as large as its equatorial disk.
On a former occasion I sent you the investigations which I had up to that time completed, including the proofs, showing that any segment bounded by a straight line and a section of a right-angled cone [parabola] is four-thirds of the triangle which has the same base with the segment and equal height. Since then certain theorems not hitherto demonstrated have occurred to me, and I have worked out the proofs of them. They are these: first, that the surface of any sphere is four times its greatest circle. . .For, though these properties also were naturally inherent in the figures all along, yet they were in fact unknown to all the many able geometers who lived before Eudoxus, and had not been observed by anyone. Now, however, it will be open to those who possess the requisite ability to examine these discoveries of mine. [Heath, 1897, Dover edition, pp. 1–2]
As this letter shows, mathematics was a “going concern” by Archimedes' time, and a community of mathematicians existed. Archimedes is known to have studied in Alexandria. He perished when his native city of Syracuse was taken by the Romans during the Second Punic War. Some of Archimedes' letters, like the one quoted above, give us a glimpse of mathematical life during his time. Despite being widely separated, the mathematicians of the time sent one another challenges and communicated their achievements.
8.3.3 Apollonius
Apollonius, about one generation younger than Archimedes, was a native of what is now Turkey. He studied in Alexandria after the time of Euclid and is also said to have taught there. He eventually settled in Pergamum (now Bergama in Turkey). He is the author of eight books on conic sections, four of which survive in Greek and three others in an Arabic translation. We know that there were originally eight books because commentators, especially Pappus, described the work and reported the number of propositions in each book.
In his prefaces, Apollonius implies that geometry was simply part of what an educated person would know, and he also implies that such people were as fascinated with it in his time as they are today about the latest scientific achievements. Among other things, he said the following.
During the time I spent with you at Pergamum I observed your eagerness to become acquainted with my work in conics. [Book I]
I undertook the investigation of this subject at the request of Naucrates the geometer, at the time when he came to Alexandria and stayed with me, and, when I had worked it out in eight books, I gave them to him at once, too hurriedly, because he was on the point of sailing; they had therefore not been thoroughly revised, indeed I had put down everything just as it occurred to me, postponing revision until the end. [Book II]
8.3.4 Zenodorus
Zenodorus (second century BCE) represents a new departure in the Euclidean tradition. Instead of proving direct proportions, as earlier mathematicians had done, he worked with inequalities and showed, as well as could be done given the tools available to him, that a regular polygon encloses a larger area than any other polygon of the same perimeter and the same number of sides, that the more sides a regular polygon of a given perimeter has, the greater the area it encloses, and that a circle encloses a larger area than any polygon whose perimeter equals the circumference of the circle. He also established similar theorems for polyhedra and spheres. These isoperimetric problems are not found in Euclid or Apollonius, and Archimedes only hints at them when he points out the need to assume that a convex curve enclosing another convex curve must be longer than the one it encloses. These results of Zenodorus are known because Theon of Alexandria quoted them in his commentary on Ptolemy's Sýntaxis. Pappus borrowed freely from Zenodorus in his own work on such problems.
8.3.5 Heron
This mathematician and engineer (first century CE) is also known as Hero (just as Plato is actually known in Greek as Platon). The name Heron was very common in his world, and it is difficult to be sure that a person by that name is any particular Heron one might have in mind. The one we shall be discussing is famous for having invented a steam engine of sorts, but we shall be interested only in the way that he represents the return of metric concepts to geometry, using numbers to describe the lengths of the sides of a triangle, for example, and giving a method of computing the area of a triangle knowing the lengths of its sides.
8.3.6 Ptolemy
Claudius Ptolemy was primarily an astronomer and physicist, although these subjects were hardly distinct from mathematics in his time. He lived in Alexandria during the second century, as is known from the astronomical observations that he made between 127 and 141 CE. He created an intricate and workable earth-centered mathematical system of explaining the motion of the planets and systematized it in a treatise known as the Sýntaxis (treatise, literally arrangement), which consisted of 13 books. Ptolemy's Sýntaxis became a classic reference and was used for well over a thousand years as the definitive work on mathematical astronomy. It became known as the “greatest” work (megíst in Greek) on astronomy and, when translated into Arabic, became al-megista or the Almagest, as we know it today.
8.3.7 Diophantus
Little is known about this author of a remarkable treatise on what we now call algebra and number theory. He probably lived in the third century CE, although some experts believe he lived earlier than that. His treatise is of no practical value in science or commerce, but its problems inspired number theorists during the seventeenth century and led to the long-standing conjecture known as Fermat's last theorem. The 1968 discovery of what may be four books from this treatise that were long considered lost was the subject of a debate among the experts, some of whom believed the books might be commentaries, perhaps written by the late fourth-century commentator Hypatia. If so, they would be the only work by Hypatia still in existence.
8.3.8 Pappus
Pappus, who is known to have observed a solar eclipse in Alexandria in 320 CE, was the most original and creative of the later commentators on Greek geometry and arithmetic. His Synag
g (Collection) consists of eight books of insightful theorems on arithmetic and geometry, as well as commentary on the works of other authors. In some cases where works of Euclid, Apollonius, and others have been lost, this commentary tells something about these works. Pappus usually writes as if the reader will have a natural interest in his subject matter, but occasionally he gives in addition a practical justification for his study, as in Book 8:
The science of mechanics, my dear Hermodorus, has many important uses in practical life, and is held by philosophers to be worthy of the highest esteem, and is zealously studied by mathematicians, because it takes almost first place in dealing with the nature of the material elements of the universe. [Thomas, 1941, p. 615]
8.3.9 Theon and Hypatia
The later commentators Theon of Alexandria (late fourth century) and his daughter Hypatia (ca. 370–415) also produced respectable work, including a standard edition of Euclid's Elements. Several of Theon's commentaries still exist, but nothing authored by Hypatia has been preserved, unless the books of Diophantus mentioned above were written by her. Very little of value can be found in Greek mathematics after the fourth century. As Gow (1884, p. 308) says:
The Collection of Pappus is not cited by any of his successors, and none of them attempted to make the slightest use of the proofs and aperçus in which the book abounds. . .His work is only the last convulsive effort of Greek geometry which was now nearly dead and was never effectually revived.
Questions
Historical Questions
8.1 Describe in general terms the periods of development, flourishing, and decline in ancient Greek mathematics, naming the primary authors and their works.
8.2 Who are the commentators who provide the context of the major works of ancient Greek mathematics?
8.3 In what way does ancient Greek mathematics differ from the mathematics of Mesopotamia and Egypt?
Questions for Reflection
8.4 What advantages can you see in an axiomatic development of mathematics starting from definitions and assumptions? Are there disadvantages?
8.5 Given that we have no documents from the time of Greek mathematics—the earliest manuscripts we have are medieval—how can we be sure that the texts we have are actually what the authors wrote? Were the copyists who wrote the early medieval manuscripts simply concerned with reproducing the text faithfully, or is it possible that they tried to improve it by revisions they thought of themselves? How could we know if they did?
8.6 Plato thought that mathematics was a sort of entranceway into the ideal world of his forms; and he also thought that the physical world, though corrupt, could be understood by relations grasped by the mind rather than the senses. To what extent is this view plausible? Does modern theoretical physics presume something similar?
Notes
1. As mentioned in the preceding chapter, some authors claim that the surface in question was actually half of a cylinder, but the words used seem more consistent with a hemisphere. In either case it was a curved surface.
2. Shakespeare relied on Plutarch's account of the life of Julius Caesar, even describing the miraculous omens that Plutarch reported as having occurred just before Caesar's death.
3. The documents from which all this semi-legendary history is assembled are widely scattered. Plutarch, in his Discourses on the Seven Sages, Stephanus page 147, section A, said that Thales drove a stake into the ground and used the proportion between the shadows of the stake and the pyramid to compute the height. Diogenes Laertius, in his Lives of Eminent Philosophers, Book 1, Section 27, reported a statement by the philosopher Hieronymus of Rhodes (third century BCE) that Thales waited until the length of his own shadow equaled his own height, then measured the length of the shadow of the Great Pyramid. He also reported (Book 1, section 24) the first-century Roman historian Pamphila as saying that Thales was the first to inscribe a right triangle in a circle. He went on to say that others attribute this construction to Pythagoras. (As a matter of general information, Stephanus pagination refers to a definitive sixteenth-century edition of the works of Plato and Plutarch by Henri Estienne (ca. 1530–1598), whose Latin name was Henricus Stephanus.)
4. Like modern cults, the Pythagoreans seem to have attracted young people, to the despair of their parents. Accepting new members from among the local youth probably aroused the wrath of the citizenry.
5. Gellius remarks at this point that the word mathmatikoí was being inappropriately used in popular speech to denote a “Chaldean” (astrologer, from a common association with the Chaldean civilization).