Basic Math and Pre-Algebra
PART 1. The World of Numbers
CHAPTER 4. Factors and Multiples
In any multiplication problem, the numbers being multiplied are factors and the result of the multiplication is the product. We’ve used that language in earlier chapters. You can also say that the product is a multiple of each of the factors. It’s time to take a step beyond the vocabulary now and look at factors and multiples in more detail. It may seem odd to give a whole chapter to multiplication, but ideas that have to do with factors and multiples come up in so many situations that it’s wise to take the time to look at all of them.
In this chapter, we’ll look at numbers that have many factors and those that have few. You’ll practice different ways to find all the possible factors of a number and work at expressing a number as the product of factors, using the smallest possible factors. Exponents will show up again to help you write those factors efficiently. All this talk about factors will lead to two important ideas: the greatest common factor and the least common multiple of two or more numbers.
Prime Numbers
When you multiply 1 by any number, the product is that number. 1 x 4 = 4, 1 x 17 = 17, and 1 x 132 = 132. The number 1 is a factor of any number. When you write a multiplication problem like those, with 1 as a factor, the other factor is always the same as the product. So if 1 is a factor of 4, then 4 is also a factor of 4, and that’s the case for any number. Any number x 1 = that number. The number 1 is a factor of every number, and every number is a factor of itself. Every number can be written as itself times 1.
All that multiplying by 1 may seem boring, and many numbers have other factors that make more interesting problems. The number 6, in addition to being 1 X 6 is also equal to 2 x 3. And some numbers have lots of possible factors. 24 could be 1 x 24, 2 x 12, 3 x 8, or 4 x 6. But there are numbers that only have one set of factors. Numbers whose only possible factors are themselves and 1 are called prime numbers. Numbers that have other possible factors besides themselves and 1 are called composite numbers. You might think that only small numbers like 2 and 3 are prime numbers, but that’s not the case.
DEFINITION
A prime number is a whole number whose only factors are itself and 1. A composite number is a whole number that is not prime because it has factors other than itself and 1.
You can use blocks to help you visualize this concept. If you have a prime number of blocks, there’s only one rectangle you can make. Try to rearrange and you just can’t get a rectangle.
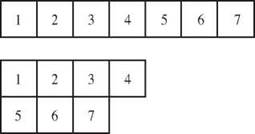
The number 7 is a prime number.
With a composite number of blocks, you can always make at least two rectangles.
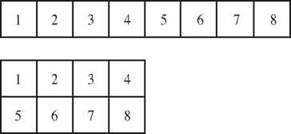
The number 8 is a composite number.
MATH TRAP
Most people think 1 is a prime number. Most people are wrong. It's understandable. The number 1 has no other factors, but it doesn't quite fit the definition of prime. Its factors aren't itself and 1. They're itself and itself, or 1 and 1. It's sort of strange, but it gets its own category. The number 1 is neither prime nor composite. It's called a unit.
Finding Prime Numbers
Take a look at the following chart, which shows the whole numbers 1 through 50. You know 2 is prime, because its only factors are 2 and 1, but all the other even numbers have 2 as a factor, so they’re composite. Multiples of 2 can be blocked out.
The number 3 is prime, but all multiples of 3 are composite, and 5 is prime, but any other number that ends in 5 is composite because it’s divisible by 5. All the multiples of 3 or 5 that haven’t already been eliminated can be blocked out.
The numbers 4 and 6 have already been marked as composite, but 7 is prime. Several multiples of 7 have already been eliminated as composite. You just need to mark 7 X 7, or 49, as composite, and believe it or not, everything left is prime, except for 1, which is in a class by itself. That means 16 of the first 50 counting numbers are prime.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
WORLDLY WISDOM
As the numbers get bigger, prime numbers become fewer and more spread out, but mathematicians are still finding them. The largest known prime number is 257,885,161 - 1, a number with 17,425,170 digits.
How do you know if a large number is prime? You won’t need to worry about extremely large numbers with thousands of digits, but you may need to know about numbers in the hundreds or thousands. Is 136 prime? How about 2,485? What about 901?
Sometimes it’s easy to tell. The number 136 can’t be prime because it’s even, so it has 2 as a factor as well as itself and 1. In the same way, 2,485 ends in 5, so it’s divisible by 5 and therefore not prime. The number 901 is harder. It’s not even, and it’s not a multiple of 5, because it doesn’t end in 5 or 0, but what about other numbers? Does it have any divisors?
There are a few shortcuts, like recognizing even numbers (numbers that end in 0, 2, 4, 6, or 8) and multiples of 5 (numbers that end in 5 or 0). You can check if a number is divisible by 3 by adding the digits. If the sum is divisible by 3, so is the original number. If you get a large number as the sum of the digits and you don’t know if it’s divisible by 3, you can add the digits again. You can add the digits as many times as necessary until you can decide if the sum is a multiple of 3.
For example, to see if 45,829 is a multiple of 3, add 4 + 5 + 8 + 2 + 9 = 28. Is 28 a multiple of 3? It’s not, but if you’re not sure, add 2 + 8 = 10. You know 10 is not a multiple of 3, so 45,829 is not a multiple of 3.
The same idea will work for 9. If you add the digits and get a multiple of 9, the original number is divisible by 9. Here’s a chart of the tests you might want to remember.
Tests for Divisibility
|
Multiple of: |
Test |
Example |
|
2 |
Ends in 2, 4, 6, 8, or 0. |
45,938 is a multiple of 2 because it ends in 8. 673 is not a multiple of 2. |
|
3 |
Sum of the digits is divisible by 3. |
9,348 is a multiple of 3 because 9 + 3 + 4 + 8 = 24, which is a multiple of 3. (Check 2 + 4 = 6, a multiple of 3.) |
|
4 |
The last two digits are a multiple of 4. |
35,712 is a multiple of 4 because the last two digits, 12, is a multiple of 4. |
|
5 |
Ends in 5 or 0. |
74,935 and 680 are multiples of 5. |
|
6 |
If it’s a multiple of 2 and a multiple of 3, it’s a multiple of 6. |
65,814 is a multiple of 2 because it ends in 4. It’s a multiple of 3 because 6 + 5 + 8 + 1 + 4 = 24, a multiple of 3. So 65,814 is a multiple of 6. |
|
8 |
The last 3 digits are a multiple of 8. |
42,864 is a multiple of 8 because 864 is a multiple of 8. |
|
9 |
Sum of the digits is a multiple of 9. |
39,348 is a multiple of 9, because 3 + 9 + 3 + 4 + 8 = 27, a multiple of 9. |
|
10 |
Ends in 0. |
483,940 is a multiple of 10. |
Sometimes, to find out if a number has any factors, or divisors, other than itself and 1, you have no choice but to just divide by each of the primes. The number 901 is not even, so 2 is not a factor. Its digits add to 10, so it’s not divisible by 3. It doesn’t end in 5 or 0, so it’s not a multiple of 5. But you just have to divide by 7 and see what happens. 901 ÷ 7 = 128 with 5 left over, so 7 is not a factor. 11 is the next prime, but 901 ÷ 11 is 81 with 10 left over, so 11 is not a factor.
But how will you know when you’ve checked enough prime numbers? One way to tell is by comparing the quotient to the divisor. If the quotient is equal to or smaller than the divisor, you can stop. You’ve checked enough. And if you get to the point where the quotient is less than or equal to the divisor and you haven’t found a factor, your number is prime.
901 ÷ 11 is 81 with 10 left over, and the quotient of 81 is larger than the divisor of 11, so this one isn’t done yet.
901 ÷ 13 = 69 with 4 left over, and the quotient of 69 is larger than the divisor of 13, so we keep going.
901 ÷ 17 = 53 exactly, which means 901 is a composite number. It can be written as 17 x 53 as well as 901 x 1.
Consider Square Numbers
When you multiply any integer by itself, the result is a square number. The expression comes from the fact that a square has the same length as width, so when you find its area, you multiply a number by itself. The number 16 is a square number because it’s equal to 42 or 4 x 4, and that’s the area of a square with a side 4 units long.
DEFINITION
Square numbers are numbers created by multiplying a number by itself, or raising it to the second power. For example, 36 is a square number. It can be written as 62 or 6 x 6.
If you know the square numbers, it will help you see how far you have to go when checking whether a number is prime. 30 x 30, or 302, is 900, which is very close to 901. The biggest prime you’ll have to try is the one just above that, or 31. If you know your square numbers, it’s easy to know how many primes you need to divide by before declaring a number prime. If you want to know if 147 is prime, think about square numbers near 147. The number 144 is 122, so if you go to the next prime after 12, that’s enough. Once you divide 147 by 13, if you haven’t found a factor, you can say 147 is prime.
Suppose you want to know if 67 is prime. If you know that 82 is 64, you only have to check 2, 3, 5, 7, and maybe 11. The number 67 is not even, so it’s not divisible by 2. Its digits add to 13, so it’s not divisible by 3. It doesn’t end in 5 or 0, so it’s not a multiple of 5. When you divide 67 by 7, you get 9 with 4 left over, so 7 is not a factor. 67 ÷ 11 is 6 (smaller than the divisor) but with 1 left over. 67 is a prime.
CHECK POINT
Decide if each number is prime or composite. If it’s composite, give a pair of factors other than the number and 1.
1. 51
2. 91
3. 173
4. 229
5. 5,229