Basic Math and Pre-Algebra

PART 1. The World of Numbers

CHAPTER 4. Factors and Multiples

Prime Factorization

Factoring is the process of starting with the product and finding the factors that produced it. (Factoring is related to division, but not quite the same.) You could factor 24 by writing it as 2 x 12, or 3 x 8, or 2 x 3 x 4, and other possibilities.

A number can have lots of different factorizations, but it has only one prime factorization. A prime factorization expresses the number as a product of only prime numbers. The prime factorization of 24 is 2 x 2 x 2 x 3.

DEFINITION

The prime factorization of a number is a multiplication that uses only prime numbers and produces the original number as its product.

You can find the prime factorization just by finding primes that are factors of the number by trial and error, but having a way to organize the search does make things faster. One method for finding the prime factorization of a number is called a factor tree.

Factor Trees

A factor tree is a device that allows you to start with any two factors of a number and to work in an organized fashion to the prime factorization.

DEFINITION

A factor tree is a method of finding the prime factorization of a number by starting with a pair of factors and then factoring each of those numbers, continuing until no possible factoring remains.

Let’s look at the prime factorization of 180 as an example. Start with any pair of factors of 180 that you can recall, maybe 18 and 10. Put 180 at the top of the tree and make a branch for 18 and a branch for 10.

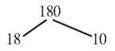
Focus on the 18 branch. Can you find factors for 18? 2 and 9 will work. Add them as branches under 18.

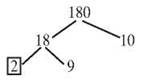
Is 2 a prime? Yes, so mark it with a circle or a box. That branch is done. Is 9 prime? No, but it factors to 3 x 3, and 3 is prime. The tree needs branches under the nine.

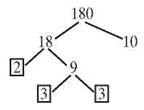
When that branch is down to primes, turn to the 10 branch. 10 = 2 x 5, and both of those numbers are prime.

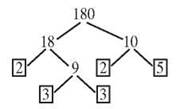
Collect all the primes you marked and you have the prime factorization of 180. 180 = 2 x 2 x 3 x 3 x 5.

CHECK POINT

Use a factor tree to help you find the prime factorization of each number.

6. 78

7. 98

8. 189

9. 255

10. 512

Using Exponents

Some prime factorizations are easy to write. The prime factorization of 42 is 2 x 3 x 7, which is short and clear. However, the prime factorization of 128 is another story. 128 = 2 x 2 x 2 x 2 x 2 x 2 x 2. It uses easy numbers, but it uses so many of them that it can get confusing. Is that six 2s or seven? It’s easy to make a mistake.

That’s why you may want to use exponents to condense the prime factorization and make it easier to understand. The prime factorization of 40 = 2 x 2 x 2 x 5, but it could be written as 40 = 2³ x 5. The exponent of 3 says to use 2 as a factor 3 times. With that notation, you can write the prime factorization of 128 as 128 = 2⁷ and know for certain that it was seven 2s.

CHECK POINT

Use exponents to write the prime factorization of each number in a compact form.

11. 200

12. 168

13. 672

14. 2,205

15. 22,000

Finding the prime factorization of a number can be an interesting undertaking. It can be difficult, but there’s a satisfaction in getting a large number broken down to a product of primes. The truth, however, is that finding a prime factorization is not usually your final goal, but a tool to help you find two other very useful numbers: the greatest common factor and the least common multiple.