Basic Math and Pre-Algebra
PART 1. The World of Numbers
CHAPTER 6. Decimals
Arithmetic with Decimal Fractions
Just about any work you can do with whole numbers or integers, you can do with fractions, whether they’re written as common fractions or as decimals. Because decimal fractions fit into the base ten system, many of the operations with decimals are the same as, or very similar to, the operations with whole numbers.
Adding and Subtracting Decimals
You’ve already seen that decimal fractions can be written in the same place value system we use for whole numbers. When you add or subtract whole numbers, you align the right end of the numbers. You’re actually aligning the unseen decimal points, so that digits with the same place value are under one another.
To add or subtract decimals, first arrange the numbers with the decimal points aligned one under another. This assures that you are adding the digits with the same place value. If the numbers don’t have the same number of digits after the decimal point, you can add zeros to the shorter ones. Remember that adding a trailing zero changes the way you name a number, but not what it’s worth.
Add or subtract as you would if the decimal points were not there, starting from the right, doing any carrying or borrowing just as you would for whole numbers. Add a decimal point to your answer directly under the decimal points in the problem.
For example, here’s how you add 34.82 and 9.7.
Align the decimal points and add a zero to 9.7.

Add as you normally would. The hundredths place adds to 2 hundredths, so you can just put that down, but the tenths place adds to 15 tenths, so you need to carry 1 to the ones place. You’ll carry again from ones to tens. You work right over the decimal points as though they weren’t there. Bring the decimal point straight down when you’re all done.
Subtraction works the same way. Align the decimal points, and add zeros to make the decimals the same length. Those zeros are especially important in subtraction, because you can’t subtract from a digit that isn’t there. Subtract normally, regrouping if you need to, and bring the decimal point straight down. Let’s try a subtraction example.
Subtract 184.93 - 99.781
Align the decimal points and add a trailing zero to 184.93. Subtract, starting at the right.
Regroup or borrow as you need to (and you need to a lot for this one). Bring the decimal point straight down.
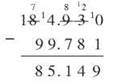
You can check your answer to a subtraction problem by adding. In the example above, check to see if 85.149 + 99.781 gives you 184.930. If it does, your subtraction is correct.
WORLDLY WISDOM
Taking a minute to estimate you answer before you do a calculation is always a good idea, and with decimals, it will help you be certain you got the decimal point in the right place. It doesn't need to be anything fancy. If you can say that you're subtracting about 185 - 100, you'll know you should be getting an answer around 85. If you get an answer more like 8 or 850, you've misplaced the decimal point.
CHECK POINT
Complete each addition or subtraction.
16. 45.9 + 19.75
17. 397.256 - 242.81
18. 17,401.12 + 15,293.101
19. 159.41006 - 143.0025
20. 1.00027 + 0.4587332
Multiplying and Dividing Decimals
Multiplying decimals requires a slightly more complicated process. It’s a good idea to estimate the product first, so if you have to multiply 3.1 x 2, you’d expect an answer around 3 x 2 or 6. If you multiply 3.1 x 0.002, you’d recognize that you’re multiplying a number around 3 by a pretty small number, quite a bit less than 1, so the answer should be less than 3, probably a lot less.
You perform the actual multiplication as though the decimal points were not present. If you were multiplying 3.1 times 2, you would first think of it as 31 times 2. (You would also think of 3.1 times 0.002 as 31 times 2 to begin. The difference comes in placing the decimal point.)
To place the decimal point in the product, first count the number of digits to the right of the decimal point in each of the factors being multiplied. Add these counts up to find the number of decimal places in the product. Start from the far right end of the answer and count to the left to place your decimal point.
For example, multiply 3.1 x 2.
The first factor, 3.1, has one digit after the decimal point. The second factor, 2, has none, so the product will have one digit after the decimal point.
Once you know that, multiply as if the decimal point wasn’t there. 31 x 2 = 62. Then place the decimal point so that your answer has one digit after the decimal point. 3.1 x 2 = 6.2.
You estimated the answer as approximately 6, so 6.2 sounds quite reasonable. Let’s look at one where the multiplier is smaller.
Multiply 3.1 x 0.002.
This problem has the same important digits, so you’ll still start by thinking that 31 x 2 = 62, but the decimal points are positioned differently.
Count the decimal places. There is one digit after the decimal point in 3.1. There are three digits after the decimal point in 0.002, so the answer must have a total of 4 digits after the decimal point. Start from the right side and count to the left. The 2 in 62 is one digit, the 6 is a second, but there must be 4 digits to the right of the decimal point so place zeros for the third and fourth, giving an answer of 3.1 x .002 = .0062.
Once again, it’s traditional to put a zero in the ones place, so 3.1 x 0.002 = 0.0062.
WORLDLY WISDOM
Just as you can add trailing zeros at the right end of a decimal without changing its value, you can add zeros at the left of a number. 87 and 087 describe the same number, but with whole numbers you don't need that zero in front. When you're placing a decimal point you might. If you run out of digits, add zeros to the left end of the number until you have enough places.
To multiply decimals:
• Multiply the factors without regard to the decimal points.
• Count the number of digits that follow the decimal point in each factor.
• Add those counts to find the number of digits after the decimal point in the product.
• Start from the right end of the product and count to the left until there are the required number of digits after the decimal point.
Just as multiplication of decimals is based on multiplication of whole numbers, with a rule for placing the decimal point, the division of decimals is based on whole number long division. But again, there will be some extra rules about decimal points. Let’s sneak up on it a little at a time.
To divide a decimal by a whole number, do your division as though both numbers were whole numbers, but then let the decimal point rise straight up into the quotient. Suppose you want to divide 54.96 ÷ 12. You’re going to divide a number close to 55 by 12. 12 x 4 = 48, and 12 x 5 = 60, so your quotient should be between 4 and 5.
Divide as if you were dividing 5,496 by 12, and for now, just let the decimal point sit between the 4 and the 9. When you’re done dividing, let the decimal point float straight up, and it will land right after the 4 in the quotient, giving you an answer of 4.58.

So if that’s how you divide a decimal by a whole number, how do you divide by a decimal? You don’t. What you do is actually to find an equivalent problem, a problem with the same answer, in which the divisor is a whole number.
That may sound like magic, but if you stop to think about it, you’ve seen equivalent problems. You know that 12 ÷ 4 = 3 and 120 ÷ 40 = 3. Those two different problems have the same answer because both the dividend and the divisor were multiplied by the same number, in that case, by 10. That will be the secret to decimal division.
MATH TRAP
When you divide decimals, the divisor needs to be a whole number. The dividend doesn't. Move the decimal point as many places as it takes to turn the divisor into a whole number. Move the decimal point in the dividend the same number of places, whether it becomes a whole number, or still has decimal digits, or needs trailing zeros added so that you can move enough. The divisor calls the play. Whatever happens to the divisor happens to the dividend.
When you multiply a decimal by 10, the decimal point moves 1 place to the right. The task of dividing 81.312 by 3.52 can also be thought of as 813.12 divided by 35.2, or 8131.2 divided by 352.
When you’re faced with a division problem where the divisor is a decimal, move the decimal point in the divisor to the right until the divisor is a whole number. Move the decimal point in the dividend the same number of places to the right. Divide normally, just as you would for whole numbers, and bring the decimal point straight up into the quotient. Here’s an example.
Divide 17.835 by 2.05.
Estimate first. A number almost 18 divided by about 2 should give you an answer close to 9.
Move the decimal point in the divisor, 2.05, two places right so that 2.05 becomes 205. Move the decimal point in 17.835 two places right as well, making it 1783.5. Then divide.

The decimal point in the dividend, between the 3 and the 5, floats straight up into the quotient for a result of 8.7.
WORLDLY WISDOM
If you've done your division and still have a remainder, you can add zeros to the dividend and keep dividing. If your dividend was a whole number and you still have a remainder when you've divided through to the ones place, add a decimal point and some zeros. Then keep dividing to get a decimal in the quotient.
Step-by-step, the process for long division of decimals looks like this:
• Make an estimate of the quotient.
• Move the decimal point to the end of the divisor.
• Move the decimal point an equal number of places in the dividend.
• Divide normally and let the decimal rise directly up into the quotient.
CHECK POINT
Complete each multiplication or division problem.
21. 4.92 x 1.5
22. 68.413 x 0.15
23. 95.94 ÷ 7.8
24. 461.44 ÷ 1.12
25. 5,066.518 ÷ 8.6
Converting Fractions
To convert a common fraction to a decimal fraction, do what the fraction tells you. No, they don’t actually talk, but every fraction is a division problem. The fraction 3/4 is the number you get when 3 is divided by 4. To change it to a decimal, do the division.
WORLDLY WISDOM
You can use the word TIBO to remind you that when you convert a fraction to a decimal, you put the top number, or numerator, inside the division sign, and the bottom number, or denominator, outside and then divide. Top In, Bottom Out, or TIBO.
To change 5/8 to a decimal, do the division problem ![]()
Add a decimal point after the 5 and add some zeros. Do the division, letting the decimal point from the dividend float straight up to the quotient.

If you’re changing a fraction to a decimal and you find that you’ve gotten several digits in the decimal form and you’re not getting a zero remainder, you’re not expected to keep dividing forever. You might carry the division one place farther than you actually want and then round your answer, understanding that this will give you an approximate, not exact, representation of the fraction.
4/7, for example, converts to 0.571428... and keeps going. You might round it to 0.571. On the other hand, you might notice that as you divide, a pattern emerges. 7/9 converts to 0.77777... and keeps repeating. To show that a pattern keeps repeating, you put a bar over the top, like this: ![]() To convert a decimal to a fraction, many times all you have to do is say the decimal’s name. The decimal 0.37 is “37 hundredths,” so write it as 37/100. If possible, simplify the fraction. The decimal 0.8 is “eight tenths,” or 8/10. That simplifies to 4/5.
To convert a decimal to a fraction, many times all you have to do is say the decimal’s name. The decimal 0.37 is “37 hundredths,” so write it as 37/100. If possible, simplify the fraction. The decimal 0.8 is “eight tenths,” or 8/10. That simplifies to 4/5.
Repeating decimals are a little trickier to convert to fractions. If you need to convert a repeating decimal like 0.12121212... or ![]() to a fraction, make the pattern (in this case, 12) your numerator, and then count the number of digits in the pattern (in this case, 2 digits). Make your denominator that many nines.
to a fraction, make the pattern (in this case, 12) your numerator, and then count the number of digits in the pattern (in this case, 2 digits). Make your denominator that many nines. ![]() is equal to 12 over 2 nines or
is equal to 12 over 2 nines or ![]() Of course, simplify if you can.
Of course, simplify if you can. ![]()
CHECK POINT
26. Change to a decimal: 4/25.
27. Change to a decimal: 7/9.
28. Change to a fraction: 0.185
29. Change to a fraction: ![]()
30. Change to a decimal: 59/8.