Basic Math and Pre-Algebra
PART 1. The World of Numbers
CHAPTER 6. Decimals
Rational and Irrational Numbers
When you met rational numbers, you might have wondered if there were any numbers that aren’t rational, and there are. They’re not whole numbers, but you can’t find a way to write them as common fractions. It’s difficult to write an irrational number, because it can’t be written as a fraction, and when you try to write it as a decimal, it goes on forever. There are rational numbers whose decimal form goes on forever, but those are repeating decimals, like 2/3 = 0.66666..., which you can write as ![]() The irrational numbers don’t have repeating patterns.
The irrational numbers don’t have repeating patterns.
Taken together, the rational numbers and the irrational numbers form the set of real numbers.
DEFINITION
Irrational numbers are numbers that cannot be written as the quotient of two integers. Real numbers is the name given to the set of all rational numbers and all irrational numbers.
Some of the irrational numbers come up when you try to take the square root of a number that isn’t a perfect square number. Taking the square root of a number means finding some number you can multiply by itself to give you this answer. The square root of 9 is 3, because 32 = 9. We write √9 = 3.
If one number can be squared to produce another, the first number is the square root of the second. The square root of 16 is 4 because 42 = 16. The symbol for square root, √, is called a radical. √16 = 4, √6.25 = 2.5, and √2 is an irrational number approximately equal to 1.414.
When you try that with a number that isn’t a square number, like 8, the answer isn’t an integer, and many times, it’s an irrational number. √8 = 2.828427125. When that happens, you either have to round that number and say, for example, that √8 is approximately 2.83 or just leave the number in square root notation: √8.
Many times your first encounter with an irrational number comes when you work with circles and meet the number called pi, or π. The reason it has a name is that it is difficult to write. It’s a number a little larger than 3, but there’s no fraction that’s exactly right, and its decimal form goes on forever without a pattern. People have used approximate values like 22/7 or 3.14, and those come close, but they’re not exactly the number we call pi. Mathematicians have worked at finding many of the decimal digits of pi. We can say that pi is approximately 3.14159265359... but it just keeps going, and as you can see, there’s no repeating pattern.
Those are the characteristics of an irrational number. It can’t be written as a fraction, because it’s not rational. When you try to find a decimal expression for it, it goes on and on and doesn’t show you any pattern.
MATH IN THE PAST
Pi is the name given to the ratio of a circle's circumference, the measurement around the circle, to its diameter, the measurement across the widest part. Pi has a long history. There is evidence that mathematicians were thinking about this number in ancient Babylon, Egypt, Israel, Greece, China, and India, but all of them came up with different values a bit more than 3. Today, mathematicians have calculated pi to trillions of digits. Still no pattern.
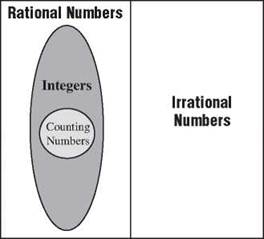
The rational numbers and the irrational numbers together make up the real numbers. The real numbers include all the other sets of numbers we’ve looked at. We started with the counting numbers and then got more complex. The irrational numbers are the first set that doesn’t overlap the ones you’ve met before.
You might picture the set of real numbers something like this:
WORLDLY WISDOM
Are there fake numbers? If the rational numbers and the irrational numbers combine to make up the real numbers, are there numbers that aren't real numbers? Actually, mathematicians will tell you that there are, but they don't call them fake. They call them imaginary numbers, because they aren't real numbers, but you can imagine them. You know that 22 = 4, and it's also true that (-2)2 = 4, but what number can you square to get -4? Most people would say there is none, but if you let yourself imagine it, there can be a √-4.
The Least You Need to Know
• The decimal point separates whole numbers on the left from fractions on the right. As you move to the right, the value of each place is divided by 10.
• To write a small number in scientific notation, write it as a number greater than or equal to 1 and less than 10 times a negative power of 10.
• Performing arithmetic operations with decimals is very similar to performing arithmetic operations with whole numbers.
• To do arithmetic with decimal fractions, work as though they were whole numbers, then follow the rules for placing the decimal point.
• To change a common fraction to a decimal, divide the numerator by the denominator.
• To change a terminating decimal to a fraction, put its digits over the appropriate power of 10. To change a repeating decimal to a fraction, put the digits in the repeating pattern over the same number of 9s.