Basic Math and Pre-Algebra

PART 1. The World of Numbers

CHAPTER 7. Ratios, Proportions, and Percentages

Calculating with Percentages

Because percentages are really ratios with a denominator of 100, they can easily be changed to fractions or decimals. To change a percentage like 44% to a fraction, just remember that percent means “out of 100.” 44% = 44/100, which simplifies to 11/25. To change a percentage to a decimal, drop the percent sign and move the decimal point two places to the left. 36.8% = 0.368 and 3% = .03. If you have a fraction and want to change it to a percentage, you can use a proportion as you did earlier, or, if you can conveniently change it to a denominator of 100, you can let it tell you what percent it is. The fraction 1/4 = 25/100 so it equals 25%, but 6/13 doesn’t easily convert to a denominator of 100, and it would be better to use the proportion method.

To change a decimal to a percentage, move the decimal point two places to the right and add a percent sign. 0.15 = 15% and 8.93 = 893%.

Yes, you can have a percentage greater than 100 percent. 100 percent is the whole thing. Percentages greater than that say you have more than the whole thing. If this week you earn 150 percent of what you earned last week, you earn all of what you earned last week (100%) and another half of that (50%).

CHECK POINT

16. Change 42% to a fraction.

17. Change 85.3% to a decimal.

18. Change 5/2 to a percentage.

19. Change 0.049 to a percentage.

20. Change 5.002 to a percentage.

Calculating Interest

Much of the time, when you encounter percentages, it’s in some kind of financial calculation. It might be a big deal, like the interest you’ll pay on your mortgage, or the interest the bank will pay you on your savings. Or it might just be leaving an appropriate tip for your server when you eat out.

Interest is money paid for the use of money. If you borrow money, you must pay it back plus additional money as a fee for the loan. If you deposit money in a bank account or invest money, you receive interest for allowing the institution to use your money. This cost of the loan is usually calculated as a percent of the amount you borrowed.

The amount borrowed or invested is the principal, and the percent of that principal that will be charged (or paid) in interest every year is the rate, sometimes called the APR, for annual percentage rate. To find the total interest on a loan or investment, you multiply the principal times the rate times the time, measured in years. The formula for simple interest is I = Prt, where I stands for interest, P for principal, r for rate, and t for time.

DEFINITION

Interest is money you pay for the use of money you borrow or money you receive because you've put your money into a bank account or other investment.

The principal is the amount of money borrowed or invested. The rate is the percent of the principal that will be paid in interest each year.

Imagine that you open a new bank account with a deposit of $4,500, and the bank pays 1.5 percent interest per year. You leave that money in the account and don’t add any money to it or take any money out for a total of 6 years. How much interest will you earn? And how much will be in your account after those 6 years?

Use the formula I = Prt, with I as the interest, P as the principal or amount you deposited, and t as 6, the time in years. Take the rate of 1.5% per year and change the percent to a fraction or decimal. You will earn I = 4,500 x 0.015 x 6 = 405. You’ll earn $405 interest, which will be added to your $4,500, so that after 6 years you’ll have $4,905.

WORLDLY WISDOM

The I = Prt formula is the calculation of simple interest. Many banks pay what's called compound interest. They calculate your interest every year (and sometimes more often) and add it to your account. The next year, if you don't disturb the money, you get interest on your original principal and on the interest. It goes on like that over and over, and each time interest is calculated you have a little more money in the bank, and you get a little bit extra interest. Over time, it can amount to quite a bit of extra money. The formula for compound interest is quite a bit more complicated and requires exponents.

If you want to plan for a special event, you might want to know how much you should deposit to earn enough interest to pay for your vacation three years from now. Or you might want to know how long it would take to earn a certain amount of interest. Those questions can be answered with the same simple interest formula, but a slightly different calculation.

Suppose you know that you need $2,000 to pay for a vacation three years from now, and you’d like that $2,000 to be the interest you earned on your savings in a bank that pays you 2 percent interest. Start with the formula I = Prt and fill in what you know. Interest is 2,000, rate is 0.02, and time is 3 years.

I = Prt

2.000  = P x 0.02 x 3

Do what arithmetic you can on the right side.

2.000  = P x 0.06

Then find P, the amount of principal you need to make that happen, by dividing 2,000 by 0.06. Don’t be discouraged when you find that you need about $33,333.33.

What if you could only deposit $5,000? How long would it take to earn $2,000 in interest? The easy answer is “a lot longer” but how long? Set up the formula with what you know. You want $2,000 in interest, you want to deposit a principal of $5,000, and the bank will pay you 2 percent per year.

I = Prt

2.000  = 5,000 x 0.02 x t

2.000  = 100 x t

2.000 ÷ 100 = t

It will take 20 years. Patience will be required.

Calculating Tax

Most countries ask their citizens to pay income tax, a percent of what they earn, to fund the government. Most states have a sales tax, a percentage of each sale that goes to fund local government. There are a great many rules about what is and isn’t subject to these taxes and under what conditions you might not have to pay them, and every country or state sets its own rate. It legislates what percent of your income or the purchase price you must pay in tax.

Whatever differences there may be, the tax is a percent of your income or a percent of your purchase. If you go out shopping and spend $273 in Colorado, the state sales tax will be 2.9 percent of your purchase. 2.9% of $273 is 0.029 x 273 = 7.917, which rounds to $7.92. That would be added on to your bill of $273, bringing your total to $273 + $7.92 = $280.92.

If you made the same purchase in Illinois, the state would ask for 6.25 percent, so your tax would be 0.0625 x 273 = 17.0625, which rounds to $17.06. That would make your bill $273 + $17.06 = $290.06.

When you go out shopping, you don’t always know exactly what the sales tax is. If you buy a jacket with a price tag that says it costs $78.95, and the cashier asks you for $83.81, you can subtract 83.81 - 78.95 = 4.86 and know that you paid $4.86 in sales tax. But what is the tax rate?

Sales tax = rate x amount of the sale, so the rate will equal the sales tax divided by the amount of the sale. Take the $4.86 you paid in tax and divide by the $78.95 cost of the jacket.

4.86 ÷ 78.95 ≈ 0.0616, or 6.16%.

MATH TRAP

The amount you pay in tax on a sale is not always just the state sales tax. Many cities add their own sales tax in addition to the state sales tax. The city sales tax will also be a percent of your purchase, but because both are added on to your bill, you may not be able to tell how much went to the city and how much to the state.

Calculating Tips

In many U.S. restaurants, the staff who serve the customers’ meals are paid a lower than usual wage and depend on tips to make up the rest of their income. Tipping began as a way to reward excellent service but has become an expected addition to the bill in many restaurants. So the question becomes, “How much should I tip?” Usually, the recommendation is that you tip your server a percentage of the bill for the meal. The recommended percent varies by region, by the type of restaurant, and by the quality of service, but is usually in the range of 15 to 20 percent.

If you and a friend have lunch at a restaurant, and the bill for your food and drinks totals $27.46, how much of a tip should you leave for your server?

If you feel that 15 percent is appropriate, you would multiply the bill amount by 0.15. 27.46 x 0.15 takes a bit of work, but it equals $4.12. If you’d rather leave a 20 percent tip, multiply 27.46 x 0.20, and the tip will be $5.49. With that information in hand, you can decide to leave somewhere between $4 and $5.50. Most people won’t worry about the pennies and will figure the tip based on the whole dollar amount.

WORLDLY WISDOM

People who know the sales tax rate in their area often use the tax to help them calculate the tip. If you know your sales tax is 5 percent of the bill, you can look at your check to see what the tax amount is. If you want to tip 15 percent, triple the tax. If you want to tip 20 percent, multiply the tax by 4. A tax rate of approximately 6 percent is fairly common, and many people triple the tax to get 18 percent of the bill. That's nicely in the 15 to 20 percent range.

To find 15 or 20 percent quickly by mental math, remember that 10 percent of a number is one tenth of the number, or the number divided by ten. Dividing by ten is just moving the decimal point one place left. 10 percent of $27.46 is $2.75 (rounded up from $2.746). Double that to find 20 percent, and the tip is $5.50, or if you want 15 percent, take half of $2.75, which is about $1.38, and add that to the $2.75, to get $4.13.

CHECK POINT

21. Find the simple interest on $18,000 invested at a rate of 4% for 5 years.

22. If you paid $130 simple interest on a loan of $1,000 for 2 years, what was the interest rate?

23. How much tax will you pay on a purchase of $175 if the sales tax rate in your area is 4.7%?

24. If the dinner bill for your family is $35.84, and you want to leave a 20% tip for your server, what is the amount of the tip you should leave?

25. A restaurant that sells a fixed price dinner for $22 per person tells you that for groups of 8 or more, they will automatically add an 18% tip to the bill. If you and seven friends plan to go for dinner, how much should each person be prepared to pay for the dinner and the tip?

Percent Increase and Percent Decrease

You’ll sometimes see an advertisement that claims there’s been a 40 percent increase in the number of vitamins in a bottle, or that there’s been a 30 percent decrease in the price of something. These are examples of percent increase or percent decrease. They compare the change, whether increase or decrease, to the original amount. And it’s amazing how many times those ads have the calculations wrong.

There’s no reason for you to get them wrong. The original amount is the whole, and the change is the part. To calculate a percent increase or a percent decrease:

• Identify the original amount. That’s the whole.

• Calculate increase or decrease. That’s the part.

• Use  to calculate the percentage.

Let’s start with an example of a percent increase.

Allison invests $800 in a stock she researched. After a year, her investment is worth $920. What is the percent increase in the value of her investment?

Original: $800

Increase: $920 - $800 = $120

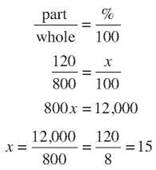
The value of her investment increased by approximately 15%.

Here’s another example. This time it’s a decrease, but your method is the same.

Melissa buys $200 worth of collectibles at a flea market and tucks them away, hoping they will increase in value. Unfortunately, when she tries to sell them, she finds they are only worth $175. What is the percent decrease in the value of her investment?

Original: $200

Decrease: $200 - $175 = $25

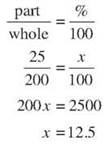
Her investment decreased approximately 12.5%.

Ready to make sure you’ve got it? Here are some for you to try.

CHECK POINT

26. George invests $500 in stock and later sells the stock for $650. By what percent did his investment increase?

27. Find the percent decrease in Sylvia’s mile time if it was 7.5 minutes when she began training and now is 6.75 minutes.

28. Paolo adopted a shelter dog who weighed 8 pounds, but by the next visit to the vet, the dog weighed 8.5 pounds. Find the percent change in the dog’s weight.

29. Find the percent decrease in Shawn’s weight if he was 180 pounds when he went out for the team and now is 150 pounds.

30. Your favorite brand of ice cream usually comes in a container that holds 1.5 quarts. If the company offers a special container that holds 2 quarts, what is your percent increase in ice cream?

The Least You Need to Know

• A ratio compares numbers by multiplying or dividing. A proportion is two equal ratios. A percentage expresses a ratio by comparing to 100.

• In any proportion, the product of the means is equal to the product of the extremes.

• Solve a proportion by filling in the known quantities and a variable for the unknown, cross-multiplying, and dividing.

• To solve percentage problems, use the rule 

• Simple interest is calculated by multiplying the principal times the rate times the time. Taxes and tips are calculated as a percentage of the total amount.