Basic Math and Pre-Algebra

PART 2. Into the Unknown

CHAPTER 8. Variables and Expressions

Dividing with Variables

When you try to divide by a variable or an expression that contains a variable, you have the same problem as you did for multiplication: you don’t know what number the variable stands for. Just as it did in multiplication, that means you can’t always do as much simplifying as you might like to, but in division, it also causes another problem. You can multiply by any number, but you can’t divide by zero. If you don’t know what number the variable stands for, you don’t know what you’re dividing by, and because division by zero is undefined, that’s dangerous.

That’s why whenever you divide by a variable or write a fraction with a variable in the denominator, you always include a note that says, in one way or another, “as long as this isn’t zero.” If you wanted to divide 5x2 ÷ x, you’d include a little warning: x ≠ 0.

Consider the Domain

When we talk about variables in algebra, we often talk about the domain of the variable. The domain is the set of all values that you can reasonably substitute for the variable. It’s all the values for the variable that make sense.

One of the first things you look at when you think about the domain is dividing. If you’re trying to divide by the variable, 0 can’t be in the domain. There are other problems to be aware of as well. You can’t take the square root of a negative number, for example, and if you’re using your variable to solve a word problem, only numbers that make sense in the problem should be in the domain. The length of a fence can’t be -10 feet, and you can’t invite 12.4 people to your party. But the number one concern is making sure you never divide by zero.

Rules for Dividing with Variables

So you have to be careful and include a warning note, but how do you divide by a variable or an expression containing a variable? There are several ways, because as the expressions get more complicated you need different methods, but the basic rules come back to fractions and exponents.

If you have a product of constants and variables divided by a product of constants and variables, you can think of the problem as a fraction that needs to be put in simplest form. Let’s look at some examples.

If you want to divide 8x by 2, you can think of it as  You’re just dividing the coefficient of the numerator by the constant in the denominator. Now it’s not hard to think of a case, like 8x/3, where it might be better to just leave it as it is, or y/5 where there’s nothing you can do. But if the denominator is a constant, and you can cancel that constant with a coefficient in the numerator, that’s what you want to do.

What if there’s a variable in the denominator? To divide 6t2/t, add your warning note, t ≠ 0, and then let the coefficient be and focus on the variables. This is where the rules for exponents come in.  provided t ≠ 0. Unless the variable in the denominator is different from the variable in the numerator, you should be able to do some simplifying with problems like this. The next step is putting the pieces together. To divide  start with the fact that y ≠ 0 and then group coefficients with coefficients and variables with variables.  Reduce the fraction, and use the rules for exponents to simplify the variable part.  You can write your final answer as y2/2 or 1/2y2, whichever you prefer, but remember to include y ≠ 0.

Dividing with Other Operations

When addition or subtraction slips into the problem, things get a little more complicated. To divide you need to break it into three fractions. Each piece of the numerator is going to be divided by the denominator.

Think for a minute about adding fractions, just regular fractions, like  First you have to change each fraction to an equivalent fraction with a common denominator, in this case, 6.  Then you’ll add the 3 + 4 and put the answer over the common denominator of 6. What you’re going to do with this variable division problem is step to when you had separate fractions with the same denominator.  is going back to  Here’s how it works. Don’t forget: x ≠ 0. 

Simplify each of the three fractions by grouping coefficients with coefficients, reducing the fraction, and then grouping variables with variables, using the rules for exponents.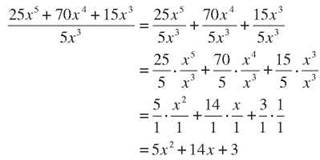 

So  as long as x is not zero.

The toughest problems are the ones in which there is addition or subtraction in the denominator. Unfortunately, they’re not as easy to break into smaller problems. If you go back to regular fractions for a minute, remember that  does not equal 

There are ways to do division problems like  but you’ll need more experience with different algebra tools before you’re ready for them. For now, practice with division problems in which the denominator does not include addition or subtraction. Reduce fractions, use the laws of exponents, and don’t forget to always add the note that says your denominator can’t be zero.

CHECK POINT

Write each quotient in simplest form.

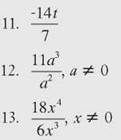
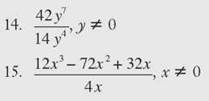
The Least You Need to Know

• Variables are letters or symbols that represent unknown numbers.

• Multiply numbers with numbers and variables with variables.

• When multiplying the same variable many times, use an exponent.

• To divide an expression by a variable, make separate fractions and reduce.

• You cannot divide another number by zero.