Basic Math and Pre-Algebra

PART 2. Into the Unknown

CHAPTER 10. Solving Equations and Inequalities

The moment you begin to use a variable to represent an unknown number, a question arises: what is the unknown number? It’s natural to want to know what number the variable represents, and in many cases, you can find out. You need to have a full mathematical sentence, called an equation or an inequality, using one variable. If you do, you can determine the value of the variable that makes the sentence true. This process is called solving the equation (or inequality).

In this chapter, you’ll look at the essential steps in working back to what a variable must equal. You’ll focus on how to clean up the problem before you start so you can use those fundamental techniques. Of course, there are special cases that need to be handled differently, and you’ll learn how to handle those. Finally, you’ll investigate what’s the same and what’s different if the mathematical sentence has a verb that talks about larger or smaller instead of just equal.

Using Equations to Find the Missing Number

Variables can stand for numbers that are unknown or numbers that change. When you use a variable to take the place of a number that changes values, you usually have an expression, the mathematical equivalent of a phrase.

For example, if you buy hamburgers for $3.50 each, the amount you have to pay will vary depending on how many burgers you buy. If you use the variable h to stand for the number of hamburgers you buy, the amount you have to pay would be represented by the expression $3.50 x h. If you buy 2 burgers, h is 2 and you pay $7. If you buy 10 burgers, h is 10 and you pay $35. There’s no one “right” value of h. It’s a different number each time you do the problem.

On the other hand, if you know that hamburgers are $3.50 each, and you know that you spent $24.50, you can write the equation $3.50 x h = $24.50. Now you have a full mathematical sentence, an equation, and a question: how many hamburgers did you buy? There’s only one value that can take the place of h and make that sentence true. Finding that value is the process of solving an equation.

DEFINITION

An expression is a mathematical phrase. Expressions may include variables, but they do not have an equals sign.

An equation is a mathematical sentence, which often contains a variable.

There are times when you can figure out what the value of the variable has to be just by using your arithmetic facts or by a little guessing and testing. You can call that solving by inspection. That’s fine when it works, but many times it’s too difficult or too time consuming. You need a better strategy.

When you have an equation, something happened to the variable. Someone multiplied, or added, or did something (or several somethings) to the variable, and you know the result. When solving an equation, your job is to undo the arithmetic that has been performed and get the variable alone, or isolated, on one side of the equation. For example, if you start with the equation 3x - 2 = 25, someone multiplied the variable by 3, then subtracted 2, and got 25. Your job is to undo that arithmetic and get to a simple “x = the original number.” In this case, x = 9.

Since you are undoing, you do the opposite of what has been done. The equation is like one of those old-fashioned scales, with a pan hanging on each side. The same amount of weight is on each pan, so the scale is balancing. To keep the equation balanced, you perform the same operation on both sides of the equation. Let’s look at each of the basic steps first and then start combining them.

Solving One-Step Equations

The simplest equations are the ones in which only one bit of arithmetic has been done to the variable. If I tell you that I picked a number and added 4 and my answer was 9, you can figure out what my number was by subtracting 4 from 9. If I pick a number, subtract 7 and get 15, you can find my number by adding. In the same way, you can undo multiplying by dividing, and undo division by multiplying. Let’s look at some examples.

Solve the equation x + 14 = 63

Because 14 was added to the original value of the variable to get 63, you want to subtract 14 to get back to the original value. To keep the balance, subtract 14 from both sides. Subtracting 14 from the left side leaves just x, and subtracting 14 from 63 tells you the value of the variable is 49.

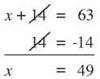
To check your solution, write the original equation and replace the variable with the number you found. If the result is a true statement, your solution is correct. In this case, x + 14 = 63 is the original equation. You put your answer of 49 in place of x and you have 49 + 14 = 63, which is true. The solution x = 49 is correct.

Here’s another example. This one asks you to undo subtraction.

Solve the equation x - 117 = 238

Someone took the number that x stands for and subtracted 117. When they were done, there was 238 left. To get back to the original value of x, you need to add 117 to both sides of the equation. This will isolate x and give you 355 as the value of x.

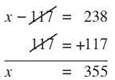
You can check your solution by starting with x - 117 = 238 and putting 355 in place of x. Because 355 - 117 = 238 is a true statement, you know your solution is correct.

Ready to try a multiplication equation? Solve the equation 19x = 28.5

Undo the multiplying by dividing. Divide both sides of the equation by 19.

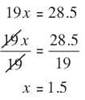
Check your solution by replacing x in the original equation with 1.5. 19x = 28.5 becomes 19(1.5) = 28.5 and that’s true, so your solution is correct.

There are four operations of arithmetic so here’s the fourth example. In this one, you see division, so use multiplication to solve it.

Solve the equation x/7= 31.

The variable was divided by 7 and the answer was 31. To find the value of the variable, multiply both sides by 7.

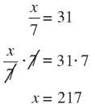
Is 217 the correct value of x? Take the original equation and replace x with 217. x/7 = 31 becomes 217/7 = 31, which is true. The solution of 217 is correct.

With those four steps, you can tackle many different equations. You’ll encounter equations that look much more complicated, but all that’s necessary is to apply these simple steps one after another.

CHECK POINT

Solve each equation.

1. x + 17 = 53

2. t - 11 = 46

3. -9a = 117

4. y/6 = -14

5. x + 14 = -3

Solving Two-Step Equations

In each of the examples we’ve looked at, just one bit of arithmetic had been done to the variable, and so only one step was necessary to isolate the variable. More often, equations have more than one step. The key to solving two-step equations is performing the correct operations in the correct order.

Remember that the variable stands for a number. Imagine that you pick a number and then perform some arithmetic with that number. You would follow the order of operations, and you’d get an answer. The equation would show what you did and the answer you got. For example, if you picked a number, multiplied it by 7 and then added 5, and got an answer of 26, the equation would be 7x + 5 = 26.

Solving an equation is undoing what was done by doing the opposite and stripping away the layers of arithmetic. To accomplish that, you need to undo things in the reverse of the order in which they were done. You undo the last bit of arithmetic first and work backward. Think about putting on your shoes and socks. You put a sock on first, then the shoe. But to take off your shoes and socks, you take the shoe off first, then the sock. It really wouldn’t work in the other order.

To solve a two-step equation, take a moment to think about what was done to the variable. Notice what operations were performed and in what order. Then perform the opposite, or inverse, operations in the opposite order. So if you see that the variable was multiplied by 4 and then 9 was subtracted, you’ll add 9 and then divide by 4. Let’s look at some examples.

Solve 5x - 11 = 5

Look at the equation and map out what happened to the variable. The number represented by x was multiplied by 5 and then 11 was subtracted from the result. The answer was 5. So what happened was multiplication by 5, then subtraction of 11. The opposite of multiplication is division and the opposite of subtraction is addition, but you also want to reverse the order. Your plan for solving the equation will be first to add 11, then to divide by 5.

Add 11 to both sides.

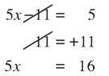
Then divide both sides by 5.

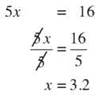
You can check your solution of x = 3.2 by substituting 3.2 into the equation to see if it makes a true statement. 5(3.2) - 11 = 5 becomes 16 - 11 = 5, which is true, so your solution is correct.

Here’s another example, with some different operations.

Solve t/4 + 3 = 7

In this equation, t is divided by 4, and then 3 is added, so the plan will be to subtract 3 and then multiply by 4. Take it one step at a time.

Subtract 3 from both sides of the equation.

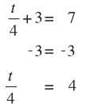
Then multiply both sides of the equation by 4.

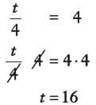
Check the solution. Is 16/4 + 3 = 7 a true 4 statement? It is, so the variable t does represent 16.

Are you ready for another example? This one is a little different, just because the order of the operations is a little different.

Solve 

In this case, the number represented by y was reduced by 7—a subtraction was performed. Then that result was divided by 3. So your plan should be first to multiply by 3, then to add 7.

Multiplying both sides by 3 will eliminate the denominator.

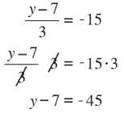
Adding 7 to both sides will isolate y and tell you the value of the variable.

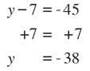
Go back to the original equation to check your solution.

 becomes  when you substitute -38 for y, and that is a true statement. The solution is correct.

WORLDLY WISDOM

A change in the order of things can sometimes make you feel confused about the solving process. An equation that's not in the order you're used to seeing, like the equation 5 - 3x = 2 can cause some trouble. When you look at what's happening in the equation, it's hard to know where to start and what happens in what order. Take a minute to rewrite the equation 5 - 3x = 2 as -3x + 5 = 2. It will be easier to plan your solution.

Let’s look at one last example. This one can be solved two different ways. Let’s look at one method here, and then we’ll tackle the other method in the next section.

Solve -3(x - 1) = -27

In this case, someone took for a number represented by x and subtracted 1 from it, then multiplied the result by -3. In the original problem, the parentheses tell you to do the subtraction first, then the multiplication. To solve the equation, you still want to do opposite operations in the opposite order, so divide by -3 and then add 1.

Undo the multiplication by dividing both sides by -3. When that’s cleared, you won’t need the parentheses anymore.

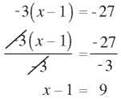
Then add 1 to both sides to find the value of x.

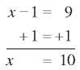
Check the solution. If x is 10 and you subtract 1, you have 9, and 9 times -3 is -27. The solution of x = 10 is correct.

CHECK POINT

Solve each equation.

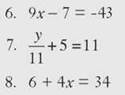
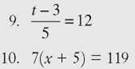
Variables on Both Sides

The basic technique for solving an equation is to do the opposite arithmetic operation to undo what’s been done to the variable. When there are two steps, you undo them in the opposite order. Those rules are almost all you need to solve equations. The one piece that’s left is how to deal with variables on both sides of the equation.

Until now, all the equations you were asked to solve had a single number, a constant, on one side. The other side had the variable and whatever was going on, and you knew you had to undo what was going on to get that variable all alone. But what if both sides of the equation had a variable? What if you had to solve 7x - 4 = 5x + 2? You still need to isolate the variable, but which one?

It’s not enough to get one of the x’s all alone. If you still have an x on the other side, you won’t know what number x represents. The key to solving an equation with variables on both sides is to eliminate one variable term first. You can eliminate either variable term. The choice is yours.

In the equation 7x - 4 = 5x + 2, you might choose to eliminate 5x. You do that by subtracting 5x from both sides. Rules about like terms are important here. You can only subtract an x-term from another x-term. You’ll subtract the 5x from the 7x.

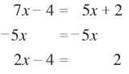
Once you’ve subtracted 5x from both sides, the second variable term is gone, and you have a two-step equation to solve.

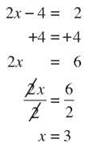
You can eliminate one variable term by adding or subtracting depending on the term you want to remove. In the equation 7 - 9x= 7x - 19, you can eliminate the variable term on the right side by subtracting lx from both sides.

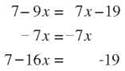
If you prefer, you can eliminate the variable term on the left side by adding 9x to both sides.

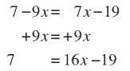
Either way, you’ll get the same solution. If an equation has variable terms on both sides, eliminate one by adding or subtracting an equivalent variable term on both sides. Then solve the equation for the remaining variable.

Simplifying Before You Solve

In an earlier example, I said there was another way to solve the equation -3(x - 1) = -27, and this is the moment to look at that method. When you solve equations, you want to be able to use those inverse, or opposite, operations, and having parentheses or extra terms can get in the way of that.

Before you begin the actual work of solving an equation, you want to make the equation as simple as possible. Focus on one side of the equation at a time, and if parentheses or other grouping symbols are present, remove them. You can do this by simplifying the expression inside the parentheses, by using the distributive property, or occasionally, by deciding that the parentheses are not necessary and just removing them. In the equation -3(x - 1) = -27, you can distribute the -3 and the equation will become -3x + 3 = -27. In the equation (5x + 2) + (3x - 4) = 14, the parentheses are really not necessary, so you can just drop them and the equation becomes 5x + 2 + 3x - 4 = 14.

Once parentheses have been cleared, take the time to combine like terms (and only like terms) before you begin solving. Each side of the equation should have no more than one variable term and one constant term when you begin to solve. So in the equation 5x + 2 + 3x - 4 = 14, you should combine the 5x and 3x and combine the +2 and the -4. The equation becomes 8x - 2 = 14.

If there are variable terms on both sides of the equation, add or subtract to eliminate one of them. Next, add or subtract to eliminate the constant term that is on the same side as the variable term. You want to have one variable term equal to one constant term. Finally, divide both sides by the coefficient of the variable term.

CHECK POINT

Solve each equation.

11. 11x + 18 = 3x - 14 

12. 5(x + 2) = 40         

13. 5(x - 4) = 7(x - 6)

14. 4(5x + 3) + x = 6(x + 2)

15. 8(x - 4) - 16 = 10(x - 7)

Special Cases

Sometimes when you try to isolate the variable, all the variable terms disappear. There are two reasons why this can happen. Sometimes you’re working with an equation that will make a true statement no matter what value you substitute for the variable. The simplest example of this is the equation x = x. No matter what you replace x with, you’ll get a true statement. Equations like this are called identities. If you subtract x from both sides of the equation, you find yourself with 0 = 0, which is true, but not the “x = a number” you were hoping for. In an identity, x can equal any number. If all the variables disappear and what’s left is true, you have an identity.

DEFINITION

An identity is an equation that is true for all real numbers.

The other reason why the variables may disappear is that you’re working with an equation that is never true. The simplest example of this kind of equation is x = x + 1. There’s no way a number could be equal to more than itself. In this case, if you subtract x from both sides you get 0 = 1, which is clearly not true. If all the variables disappear and what’s left is false, the equation has no solution.

Don’t confuse identities or equations with no solution with equations that have a solution of zero. The equation 0x = 0 is an identity, the equation 0x = 4 has no solution, but the equation 4x = 0 has a solution of x = 0.

CHECK POINT

Solve each equation. If there is no solution, say that. If all numbers are solutions, label the equation an identity.

16. 2x - 3 = x - 3

17. 6x - 4 = 2(3x - 2)

18. 9x + 11 = 3(3x + 4)

19. 5x + 13 = 22 - 4x

20. 19 - 8x = 4(5 - 2x) - 1