Basic Math and Pre-Algebra

PART 3. The Shape of the World

CHAPTER 13. Triangles

Geometry is a branch of mathematics that looks at shapes. That’s true, but “shapes” covers so much ground that the statement really doesn’t tell you much. To understand what geometry really looks at, what kinds of questions it tries to answer, you need to break that down a bit.

The first big distinction you can make is that geometry looks at shapes with straight sides, called polygons, and shapes that curve, or circles. There are some things you can say about all polygons, but the conversation gets more interesting when you start to break that group down even more according to the number of sides the polygon has.

In this chapter, we’ll explore triangles, polygons with three sides. We’ll look at some things that are true about all triangles, and then organize triangles into groups, based on facts about their sides or about their angles, or both. There will be lots to learn about right triangles, the most interesting group. We’ll also have a look at the very practical matters of area and perimeter.

Facts about Triangles

A polygon is a figure formed by connecting line segments at their endpoints until they come back to where they started. You need at least three segments to be able to close the shape, but you can make a polygon with many more sides. The line segments are called sides, and the points where the sides meet are called vertices. When two sides meet at a vertex, they form an angle.

DEFINITION

A polygon is a closed figure made up of line segments that meet at their endpoints.

The members of the family of polygons take more specific names based on the number of sides they have. A polygon with three sides is called a triangle. It has three sides, three vertices, and three angles. The prefix tri means “three.” Tri-angle = three angles. A polygon with four sides is called a quadrilateral. Quad means “four” and lateral means “side.” We’ll look at quadrilaterals in the next chapter.

Math is always interested in measuring things, and geometry is no exception. In a triangle, you can measure the sides and the angles. You can also draw and measure other line segments inside the triangle.

An altitude is a line segment that starts at a vertex of the triangle and meets the opposite side at a right angle. You measure the altitude to find the height of the triangle, so often the words altitude and height are used interchangeably.

DEFINITION

An altitude is a line segment from a vertex of a triangle perpendicular to the opposite side.

The altitude usually falls inside the triangle, but sometimes it can actually be a side of the triangle, and sometimes, if the triangle has an obtuse angle, the altitude can be outside the triangle. If that happens, you extend the opposite side to see where the altitude should stop.

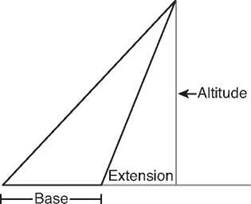
This triangle has an obtuse angle, so the altitude falls outside the triangle.

You can bisect any one of the angles in a triangle. The line segment from the vertex to the opposite side that cuts the angle into two congruent angles will not necessarily cut the opposite side in half. It’s an angle bisector, not a segment bisector.

DEFINITION

An angle bisector in a triangle is a line segment from a vertex to the opposite side that divides the angle at that vertex into two congruent angles.

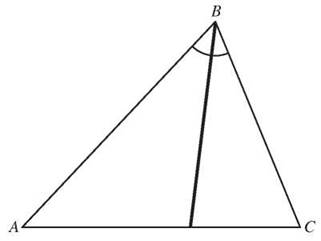
The segment drawn from angle B to side AC bisects angle B by cutting it into two angles of equal size.

The line segment from a vertex to the midpoint of the opposite side is called a median.

DEFINITION

A median of a triangle is a line segment that connects a vertex to the midpoint of the opposite side.

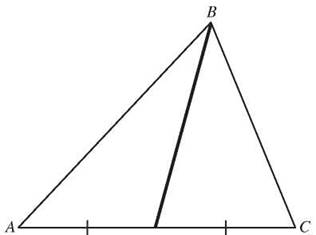
The segment drawn from angle B to the midpoint of side AC divides AC into two equal segments but does not bisect angle B.

In most triangles, the altitude, the angle bisector, and the median from a vertex are all different line segments.

It’s often the case that something is true only for some triangles, but there are things that are true about any triangle. One important one is called the Triangle Sum theorem. In any triangle, the sum of the measures of the three angles is 180°. You can see this if you cut a triangle out of paper and tear off two corners and set them next to the third corner.

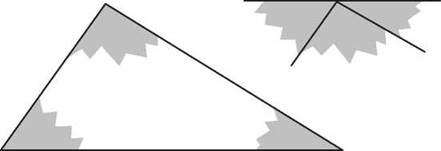
The torn corners can be put together to form a 180° angle.

If ∆ABC is a triangle with ∠B = 90°, the sum of the measures of ∠A and ∠C must be 90° because the three angles of the triangle total 180°. If ∠B measures 90°, the other two angles must make up the other 90°.

An exterior angle of a triangle is formed by extending one side of the triangle. The measure of an exterior angle of a triangle is equal to the sum of the two remote interior angles.

DEFINITION

If one side of a triangle is extended, the adjacent angle formed is called an exterior angle of the triangle.

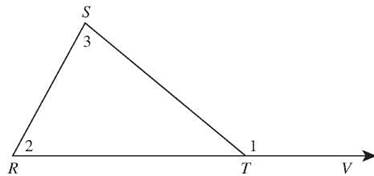
The sum of the two remote interior angles (m∠1 and m∠2) equals the measure of the exterior angle (m∠3): m∠1 + m∠2 = m∠3.

In ∆RST, m∠S = 43° and m∠R = 28° The measure of the exterior angle of the triangle at Tis equal to the sum of the two remote interior angles, ∠S and ∠R. Adding the measures of those two angles tells you the exterior angle is 43 + 28 = 71°. You could calculate the measure of ∠STR (180 - 43 - 28 = 109°), and since ∠STV is supplementary to ∠STR, it will be 180 - 109 = 71°.

So for any triangle, you know what the angles add up to, but you don’t know what the individual angles measure. When you look at sides, you can again say something that’s true all the time, but there’s a limit to how specific you can be. In any triangle, the sum of the lengths of any two sides will be greater than the length of the third. Imagine your home is at one vertex, A, of a triangle, and your best friend’s home is at another vertex, C. To get to your friend’s home, you could walk down the street from A to B and then turn the corner and follow the road from B to C. Or you could take the shortcut through the backyards straight from A to C. The shortcut is, obviously, shorter. AB + BC > AC.

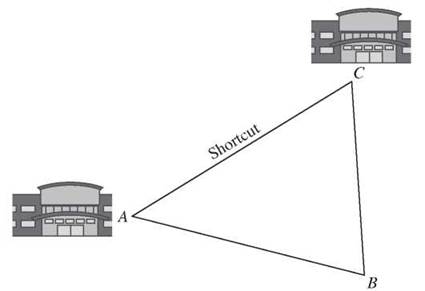
Put another way, the length of any side of a triangle is less than the sum of the other two sides. Suppose you know a triangle has sides 4 inches long and 7 inches long. Those add to 11 inches. The third side must be less than 11 inches. But turn things around a little bit. The unknown side plus the 4-inch side must be more than 7 inches, so the unknown side must be more than 3 inches. It has to be more than 3 but less than 11 inches. The length of any side of a triangle is less than the sum of the other two sides but more than the difference between them.

The longest side of a triangle is always opposite the largest angle. Remember that angles are measured by the rotation between the sides. The wider an angle opens, the longer the line segment it will take to connect the ends of the sides. The longest side is opposite the largest angle, and the shortest side is opposite the smallest angle. That, of course, means that the medium-sized side is opposite the medium-sized angle. It also means that whenever a triangle has congruent angles, the sides opposite the congruent angles are the same length.

CHECK POINT

1. In ∆RST, m∠R = 48°, and m∠T = 102°. Find the measure of ∠S.

2. In ∆RST (described in question 1), side  is extended through S to point Q to create exterior angle ∠TSQ. Find the measure of ∠TSQ.

3. In ∆RST (described in question 1), side  is extended through S to point Q to create exterior angle ∠TSQ and through R to point P to create exterior angle ∠TRP, and side  is extended through Tto point Nto form exterior angle ∠STN. Find the total of m∠TSQ + m∠TRP + m∠STN.

4. Placidville is 43 miles from Aurora, and Aurora is 37 miles from Lake Grove. The distance from Placidville to Lake Grove is at least _____ miles but less than _____ miles.

5. Gretchen lives 5 miles from the library and 2 miles from school. The distance from the library to school is between _____ miles and _____ miles.