Basic Math and Pre-Algebra
PART 3. The Shape of the World
CHAPTER 13. Triangles
Classifying Triangles
Just as trying to talk about all polygons at the same time didn’t make much sense, trying to talk about all triangles at once can be hard. It’s more practical to break the family of triangles down into categories, and you usually do that either by the sides or by the angles.
If all the sides of a triangle have different lengths, the triangle is scalene. You can’t say much else about them, except that all their angles will have different measures, too.
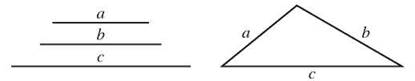
A scalene triangle has three sides of different lengths.
Isosceles triangles are triangles with two congruent sides. The two congruent sides are called the legs, and the third side is called the base. The angles opposite the congruent sides, often called the base angles, are congruent to each other. The angle between the legs is usually called the vertex angle.
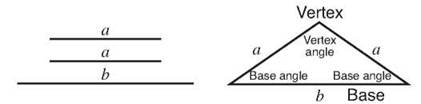
An isosceles triangle has two sides that are the same length. The congruent sides are called the legs, and the third side is the base.
The angle between the equal sides is the vertex angle, and the other two angles are base angles.
In an isosceles triangle, the altitude drawn from the vertex to the base bisects the base and the vertex angle. This is one of the few cases where one line segment does more than one job. It’s an altitude, it’s an angle bisector, and it’s a median.
An equilateral triangle is one in which all three sides are the same length. All three angles will be the same size, and because the three angles add up to 180°, each of the angles in an equilateral triangle measures 60°. Any altitude is a super segment that bisects the side to which it is drawn and the angle from which it is drawn.
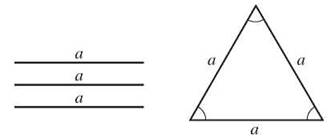
A triangle in which all three sides are the same length is an equilateral triangle. Equilateral triangles are also equiangular.
Because the three angles of an equilateral triangle are congruent, it is also described as equiangular. All three angles in an equiangular triangle measure 60°.
WORLDLY WISDOM
Is an equilateral triangle isosceles? It depends on who you talk to. Some folks will say an isosceles triangle has exactly two equal sides, so they would say no. Others will say an isosceles triangle has at least two equal sides, and their answer would be yes. The fact is, anything that's true for an isosceles triangle is true for an equilateral triangle.
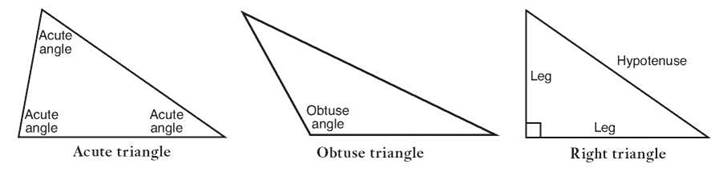
The other ways that triangles are classified by angles have to do with the sizes of the angles. If all three angles are acute angles, that is, if all three have measurements less than 90°, then you say the triangle is an acute triangle. This can happen in a scalene triangle if, for example, it has angles of 80°, 47°, and 53°, or it can happen in an equilateral triangle that has angles of 60°, 60°, and 60°. An isosceles triangle can be acute, too. For example, you might have angles of 30°, 75°, and 75°.
If a triangle has an obtuse angle, an angle greater than 90°, it’s called an obtuse triangle. The altitude of an obtuse triangle will often fall outside the triangle.
If a triangle has a right angle, it’s called a right triangle. We’ll take a closer look at right triangles in the next section.
WORLDLY WISDOM
Obtuse triangles can only have one obtuse angle, and right triangles can only have one right angle. The three angles of a triangle add up to 180°. If one angle is already 90° or more, there's 90° or less for the other two. They'll have to be acute.
CHECK POINT
6. ∆RST is isosceles with RS = ST. If m∠SRT = 39°, then m∠STR = _____.
7. In right triangle ∆ABC, ![]() and m∠C is 19°. Find m∠A.
and m∠C is 19°. Find m∠A.
8. True or False: If m∠P = 17° and m∠Q = 25°, then ∆PQR is an acute triangle.
9. If m∠P = 17° and m∠Q= 25°, then the longest side of ∆PQR is side ______.
10. If the vertex angle of an isosceles triangle measures 94°, then the base angles measure _____.