Basic Math and Pre-Algebra

PART 3. The Shape of the World

CHAPTER 14. Quadrilaterals and Other Polygons

Trapezoids

A trapezoid is a quadrilateral with one pair of parallel sides and one nonparallel pair. It looks like a triangle that lost its head. The parallel sides are called the bases, and the nonparallel sides are called the legs.

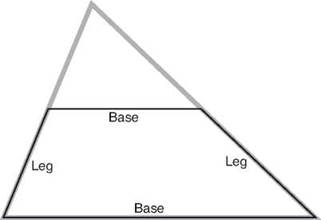
You might be able to see, with what you know about parallel lines and transversals, that the angles formed by the bases and one of the nonparallel sides are supplementary. These are called consecutive angles, but it’s important to remember that the term “consecutive angles” applies only to the two angles at either end of a leg and not to the two angles at either end of a base. Those are base angles. The consecutive angles of a trapezoid are supplementary, but the base angles are not.

If the nonparallel sides are congruent, the trapezoid is an isosceles trapezoid. You might have guessed that you get an isosceles trapezoid by cutting the top off an isosceles triangle, so you won’t be surprised to hear that the base angles of an isosceles trapezoid are congruent, just as the base angles of an isosceles triangle are congruent. But you might be surprised to know that the trapezoid has two sets of base angles: the ones at each end of the longer base and the ones at each end of the shorter base. The two angles in each set are congruent, and the angles in one set are supplementary to the angles in the other set.

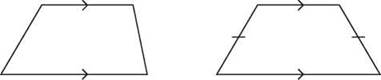
A trapezoid is a quadrilateral in which one pair of opposite sides are parallel. A trapezoid is an isosceles trapezoid if the nonparallel sides are the same length.

The line segment joining the midpoints of the nonparallel sides is called the median of the trapezoid. The median is parallel to the bases. Its length is the average of the bases.

DEFINITION

The median of a trapezoid is a line segment that connects the midpoints of the two nonparallel sides.

Like all quadrilaterals, a trapezoid has two diagonals. In an isosceles trapezoid, the diagonals are congruent. Diagonals of other trapezoids are not congruent. Diagonals of a trapezoid do not bisect one another. That belongs only to parallelograms.

CHECK POINT

11. In trapezoid ABCD,  and  is a median. AC = 14 cm and BD = 30 cm. How long is median ?

12. In trapezoid FIVE,  and m∠F = 59°. What is the measure of ∠I?

13. In trapezoid TEAR,  and TE = AR. If ∠E = 107°, find the measures of ∠A and ∠R.

14. In trapezoid ZOID,  m∠Z = 83° and m∠I = 97°. If ZO = 4 cm, how long is 

15. In trapezoid PQRT,  and  is a median. If MN = 17 inches and PT = 21 inches, how long is ?