Basic Math and Pre-Algebra
PART 3. The Shape of the World
CHAPTER 15. Circles
Circles in the Coordinate Plane
When you looked at the coordinate plane, you were interested mostly in the graphs of lines and the connection between the line and its equation. When you draw a circle on the coordinate plane, you can see that its equation has to be more complicated than the equation of a line, because the pattern of where the points fall is more complicated. But it turns out that you already know enough to figure out that equation, and it all goes back to the definition.
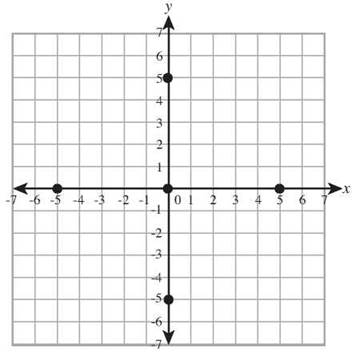
A circle is defined as the set of all points at a fixed distance from a given point. Let’s keep things simple in the beginning and use the origin as the center point. That will mean that the circle is all the points that are r units from the point (0,0) for whatever radius r you pick. Let’s have r = 5 for our example.
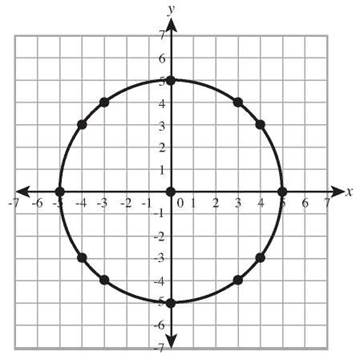
Finding the first few points is easy. From the origin, count 5 up and put a point at (0,5). Then count 5 down from the origin and put a point at (0,-5). Do a left and right move and put points at (5,0) and (-5,0). With those points you can imagine what the circle might look like, but it would be easier to draw it with a few more points.
Do you remember the distance formula? It’s the one that says the distance between two points (x1,y1) and (x2,y2) is ![]() And do you remember that the distance formula is just the Pythagorean Theorem in disguise? You know that every point on the circle is 5 units away from the origin, so if you put a 3-4-5 right triangle with one vertex at the origin and one leg along the x-axis, the other end of its hypotenuse will be 5 units from the origin.
And do you remember that the distance formula is just the Pythagorean Theorem in disguise? You know that every point on the circle is 5 units away from the origin, so if you put a 3-4-5 right triangle with one vertex at the origin and one leg along the x-axis, the other end of its hypotenuse will be 5 units from the origin.
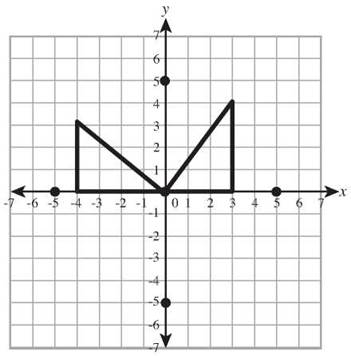
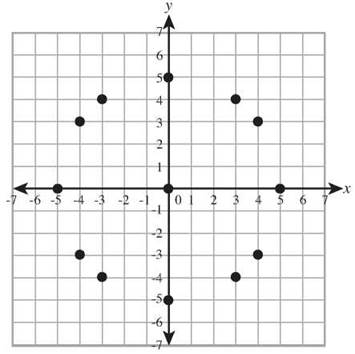
You can use that 3-4-5 right triangle like a measuring stick, putting it in different positions, and you get more points on your circle. When it looks like this, it will be easy to connect the dots.
But let’s go back to the distance formula for just another minute. ![]() You know one point is the origin, (0,0), and the distance is 5. Let’s plug those in.
You know one point is the origin, (0,0), and the distance is 5. Let’s plug those in.
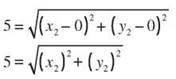
Now drop the little twos at the bottom of the x and y, and then square both sides to get rid of the square root.
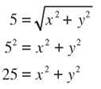
Do you know what that is? It’s the equation of the following circle—a circle with a center at (0,0) and a radius of 5.
The equation of a circle with center (0,0) and radius r is x2 + y2 = r2.
If the center isn’t at the origin, the equation gets a little more complicated, but in a way that makes sense if you remember that it came from the distance formula. Suppose you wanted a circle of radius 5 with its center at (1,4). The equation would be (x - 1)2 + (y - 4)2 = 52. The equation of a circle with center at (h,k) and radius r is (x - h)2 + (y - k)2 = r2.
CHECK POINT
21. Write the equation of a circle with its center at the origin and a radius of 3 units.
22. Graph the circle represented by the equation x2 + y2 = 64.
23. Find the center and radius of the circle represented by the equation (x - 8)2 + (x - 3)2 = 49.
24. Write the equation of a circle with center (4,9) and radius of 2 units.
25. Graph the circle represented by the equation (x - 8)2 + (y - 3)2 = 36.
The Least You Need to Know
• A circle is the set of points at a fixed distance, called the radius, from a fixed point, called the center.
• A chord is a line segment that connects two points on the circle. A diameter is the longest chord in a circle and passes through the center.
• A secant is a line that contains a chord. A tangent touches a circle at just one point.
• A central angle has its vertex at the center of a circle and is equal to its intercepted arc. An inscribed angle has its vertex on the circle and is equal to half its intercepted arc.
• When two chords intersect inside a circle, each pair of vertical angles formed is equal to half the sum of the two intercepted arcs.
• Angles formed by two secants, two tangents, or a tangent and a secant are equal to half the difference of their intercepted arcs.
• The equation of a circle with center (h,k) and radius r is (x - h)2 + (y - k)2 = r2.