Basic Math and Pre-Algebra
PART 1. The World of Numbers
CHAPTER 3. Order of Operations and Integers
In the previous chapter, we focused on arithmetic that used whole numbers. The whole numbers are the counting numbers (1, 2, 3, 4, 5, and so on) and zero, or the set {0, 1, 2, 3, 4, 5 ...}. It’s time now to look at some of the rules about how you should approach more complicated problems. In this chapter, we’ll look at the order of operations and at what people do when they don’t want you to follow those rules.
You’ve already encountered the commutative property and the associative property, the rules that let you rearrange a problem that’s all addition or all multiplication. Because your problems aren’t always one operation, it’s time to meet the distributive property, which will give you some options for dealing with addition and multiplication in the same problem and help with mental math along the way.
The set of whole numbers may contain infinitely many numbers, but even the whole numbers aren’t big enough to express all the ideas people have about numbers, so in this chapter you’ll get acquainted with a set of numbers called the integers. These positive and negative numbers let you express ideas of opposites and give you a way to answer questions you might have once been told were impossible.
Order of Operations
What does 2 + 3 x 7 equal? Some people might say 2 + 3 is 5 and 5 times 7 is 35. Those people started at the left and did what they saw as they saw it, moving across the line, a logical enough approach. Other people would do the multiplying first and say that’s 21, then add on the 2 to get 23. Those people might have thought that multiplication is repeated addition, so do that first, then the simple addition.
And what about the order of the numbers? You learned that addition is associative and commutative, so you can rearrange an addition problem. And you can rearrange a multiplication problem, too, so can you rearrange one that has both operations? Can you change 2 + 3 x 7 to 2 + 7 x 3? If you do, the multiplication-first people will get the same answer, but the left to right people will get a different one than they got the first time.
Those are great questions, and you certainly don’t want 2 + 3 x 7 to have two (or more) different values, depending on who does the arithmetic. That wouldn’t be practical. So what’s the solution?
One way to communicate what should be done first is to add parentheses. The expression (2 + 3) x 7 tells you to add first, then multiply. (2 + 3) x 7 = 5 x 7 = 35. On the other hand, 2 + (3 x 7) says multiply first, so you get 2 + (3 x 7) = 2 + 21 = 23.
That’s helpful, but you still need to know what to do, even if people writing the problem don’t use parentheses. So there’s an agreement among people who do arithmetic about what to do first, second, and so on.
That agreement is called the order of operations. What’s in parentheses will always get done first, if there are parentheses, and after that, the order will be exponents (think of them like supermultiplication), then multiplication and division, and finally addition and subtraction.
DEFINITION
The order of operations is an agreement among mathematicians that operations enclosed in parentheses or other grouping symbols should be done first, and then exponents should be evaluated. After that, do multiplication and division as you meet them moving left to right, and finally do addition and subtraction as you meet them, moving left to right.
There are a lot of memory devices to help you remember the order, and one of them, PEMDAS, is so common many people use it in place of order of operations, as if it were a name. The letters in PEMDAS are meant to help us remember to:
• P: Simplify expressions inside Parentheses
• E: Evaluate powers, or numbers with Exponents
• MD: Multiply and Divide, moving from left to right
• AS: Add and Subtract, moving from left to right
DEFINITION
PEMDAS is a mnemonic, or memory device, to help you remember that the order of operations is parentheses, exponents, multiplication and division, addition and subtraction.
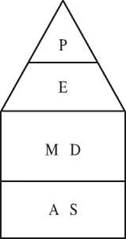
Some people use a sentence, like Please Excuse My Dear Aunt Sally, to help remember the letters in PEMDAS, and others use an image of a house. The house reminds you that multiplication and division are done together, and so are addition and subtraction.
MATH TRAP
Multiplication and division have the same priority. Don't do all the multiplication and then all the division. Do multiplication or division as you meet them as you work across the line. The same is true for addition and subtraction. Do them as you come to them.
Here are some examples of the order of operations at work. Look at each example first, and think about what you would do. Then read the explanation to see if you had all the rules in order.
Example 1: Simplify (4 x 52 - 8) x 3
There are parentheses here, so work on what’s inside them first. It’s a little problem of its own, so follow the order of operations. First is the exponent. The exponent of 2 on the 5 tells you to multiply 5 x 5. That makes the problem (4 x 25 - 8) x 3. Do the multiplication inside the parentheses, and you have (100 - 8) x 3. Then you can subtract to get 92 x 3. That gives you 276.
Ready for a more complicated problem? Try this example.
Example 2: 7 x 20 - 2 x 4 + 32 + 12 ÷ 4
There are no parentheses, so take care of the exponent first. 32 = 9, so the problem becomes 7 x 20 - 2 x 4 + 9 + 12 ÷ 4. Next, do multiplication and division as you come to them, starting on the left and moving across the line: first 7 x 20, then 2 x 4, and then 12 ÷ 4.
7 x 20 - 2 x 4 + 9 + 12 ÷ 4
= 140 - 2 x 4 + 9 + 12 ÷ 4
= 140 - 8 + 9 + 12 ÷ 4
= 140 - 8 + 9 + 3
When all the multiplying and dividing are taken care of, return to the beginning of the line, and do addition and subtraction as you come to them.
140 - 8 + 9 + 3
= 132 + 9 + 3
= 141 + 3
= 144
Sometimes you’ll see more than one set of grouping symbols in the same problem, and sometimes you may see one set inside another. Different types of grouping symbols are often used to help you tell which is which.
Example 3: 7[120 - 2(4 + 3)2 + 12] ÷ 2
This problem uses parentheses inside of brackets. Brackets have the same meaning as parentheses. They’re just a different shape so you don’t get confused. Work from the inside out. Notice that there are numbers in front of the parentheses and brackets with no operation sign in between. This is another way of writing multiplication.
Do what’s in the parentheses first.
7[120 - 2(4 + 3)2 + 12] ÷ 2
= 7[120 - 2(7)2 + 12] ÷ 2
Now work on the problem inside the brackets: 120 - 2(7)2 + 12. Follow the order of operations and don’t worry about anything else until you finish with this part.
7[120 - 2(7)2 + 12] ÷ 2
= 7[120 - 2(49) + 12] ÷ 2
= 7[120 - 98 + 12] ÷ 2
= 7[120 - 98 + 12] ÷ 2
= 7[22 + 12] ÷ 2
= 7[34] ÷ 2
Now you can finish up, starting from the left.
7[34] ÷ 2
= 238 ÷ 2
= 119
Although a problem may look complicated, using the order of operations can break it down into manageable steps.
WORLDLY WISDOM
A number written in front of parentheses or other grouping symbols without an operation sign in between tells you to multiply that number by the result of the work in parentheses. For example, 3(4 - 2) = 3(2) = 3 x 2 = 6.
A minus sign in front of parentheses tells you to subtract the result of the parentheses from the number that precedes the minus sign. For example, 10 - (5 + 1) = 10 - (6) = 10 - 6 = 4.
Try applying the order of operations to some problems.
CHECK POINT
Complete each arithmetic problem.
1. 9 - 4 x 2
2. 32 - 2 x 4 + 1
3. (23 - 5) x 2 + 14 ÷ 7 - (5 + 1)
4. [(23 -5) x 2 + 14] ÷ 5 - 3 + 1
5. [(32 -2 x 4) + 1]2 + [11 - 8 + 5(3 + 1)]