Basic Math and Pre-Algebra

PART 3. The Shape of the World

CHAPTER 17. Geometry at Work

Indirect Measurement with Trigonometry

Trigonometry, or “triangle measurement,” developed as a means to calculate lengths that can’t be measured directly. It accomplishes this by using the relationships of sides of right triangles. These fundamental relationships of trigonometry are based on the proportions of similar triangles.

Trigonometric Ratios

If you look at two right triangles, each with an acute angle of 25°, you can quickly prove that the two triangles are similar. The 25° angles are congruent and the right angles are congruent, so the triangles are similar. In fact, all right triangles containing an angle of 25° are similar, and you can think of them as a family. For any right triangle in this family, the ratio of the side opposite the 25° angle to the hypotenuse will always be the same.

That’s not the ratio you usually think about with similar triangles, but it follows from the usual one. Most of the time, you’d say that the ratio of the side opposite the 25° angle in one triangle to the side opposite the 25° angle in the other is the same as the ratio of the hypotenuse to the hypotenuse. Lets write it this way:   If you cross-multiply, divide both sides by hypotenuse1, and then divide both sides by hypotenuse2, here’s what happens.

The ratio of the side opposite the 25° angle to the hypotenuse is the same in every right triangle in the 25° family. The ratios of other pairs of sides will remain constant throughout the 25° family, and it’s not limited to just the 25° family. The ratios of pairs of sides are the same for all the right triangles in any family. Trigonometry takes advantage of that fact and gives a name to each of the possible ratios.

If the three sides of the right angle are labeled as the hypotenuse, the side opposite a particular acute angle, A, and the side adjacent to the acute angle A, six different ratios are possible. Three are commonly used. The other three are the reciprocals of the first three, and while it’s nice to know they exist in case you ever need them, you can just deal with the three basic ratios called the sine, cosine, and tangent.

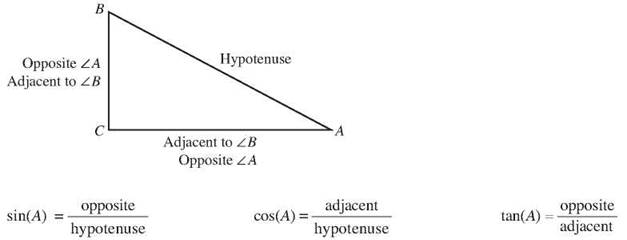
Getting the definitions of the three principal trig ratios right is critical for your problem solving, so it helps to have a memory device, or mnemonic, to help you remember them. Many people like the word SOHCAHTOA to remember the trig ratios. It stands for Sine = Opposite/Hypotenuse; Cosine = Adjacent/Hypotenuse; Tangent = Opposite/Adjacent.

CHECK POINT

21. sin ∠A

22. tan ∠B

23. cos ∠A

24. tan ∠A

25. sin ∠B

Finding Missing Sides

With these three ratios and a table of their values (or a calculator that has keys for them), it is possible to solve for any unknown side of the right triangle if another side and an acute angle are known, or to find the angle if two sides are known.

MATH IN THE PAST

Once upon a time, students had to rely on tables to look up the values of the ratios for each family of right triangles, but now the sine, cosine, and tangent of an angle can be found with a few keystrokes on your calculator. Because the other three ratios don't have keys on the calculator, they're not used as often.

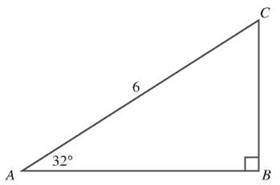
In right triangle ∆ABC, hypotenuse  is 6 cm long, and ∠A measures 32°. To find the length of the shorter leg, it helps to first make a sketch to help you visualize the triangle. The shorter leg will be opposite the smaller angle, so if you draw the triangle and calculate the measure of each angle, you’ll see that m∠A = 32°, m∠B = 90°, and m∠C = 58°. You need to find the side opposite the 32° angle, or side 

You need a ratio that talks about the opposite side and the hypotenuse (because that’s the side you know). The sine is the one you want.  From your calculator, you can find that  The side opposite the 32° angle is about 3.2 cm.

Remember that tree you measured by using similar triangles? You needed the help of a friend to make the second triangle, but what if your friend wasn’t available? What would you have done?

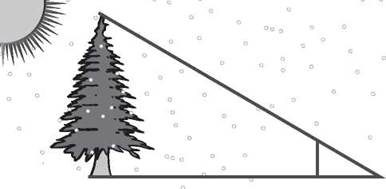
With the help of trigonometry, you could find the height of the tree without your friend. Stand at the tip of the tree’s shadow and measure the angle to the top of the tree. The height of the tree is the side opposite that angle, and the length of the shadow is the side adjacent to the shadow. The opposite side over the adjacent side forms the ratio called the tangent.

In this case, you’d probably find the angle to be about 68°, and you know the length of the tree’s shadow is 30 feet. You can find tan(68°) on a table or calculator and set up the problem like this.

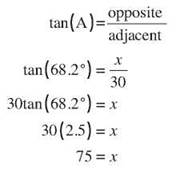
Once again, the tree is 75 feet high.

CHECK POINT

26. ∆XYZ is a right triangle with right angle ∠Y and hypotenuse  equal to 42 cm. If ∠X measures 56°, find the length of side  to the nearest centimeter.

27. ∆ABC is a right triangle with right angle ∠C, ∠A = 46°, and side  is 42 cm long. Find the length of  to the nearest centimeter.

28. In right ∆RST, ∠S is a right angle and RT = 24. If ∠T measures 30°, find the length of  to the nearest centimeter.

29. In right ∆ABC with right angle at C, ∠B = 76°, and side  is 80 feet. Find the length of hypotenuse 

30. In right ∆XYZ with right angle at Y, ∠X = 32°, and side  is 58 cm. Find the length of  to the nearest centimeter.

The Least You Need to Know

• To find the area of irregular figures, find the area of the whole figure and subtract the area of the unshaded portions, or divide the area into shapes whose areas can be calculated and add the results.

• When triangles are similar, corresponding sides are in proportion, and those proportions can be used to find the lengths of unknown sides.

• Trigonometric ratios, based on families of similar right triangles, can be used to find unknown sides of right angles.

• For any acute angle A in a right triangle, sin(∠A) = length of the opposite side divided by the length of the hypotenuse, cos(∠A) = length of the adjacent side divided by the length of the hypotenuse, and tan(∠A) = length of the opposite side divided by the length of the adjacent side.