Basic Math and Pre-Algebra

APPENDIX A. Check Point Answers

Chapter 1

1. In the number 3,492, the 9 is worth 9 tens.

2. In the number 45,923,881, the 5 is worth 5 millions.

3. In the number 842,691, the 6 is worth 6 hundreds.

4. In the number 7,835,142, the 3 is worth 3 ten-thousands.

5. In the number 7,835,142, the 7 is worth 7 millions.

6. 79,038: seventy-nine thousand, thirty-eight

7. 84,153,402: eighty-four million, one hundred fifty-three thousand, four hundred two

8. “eight hundred thirty-two thousand, six hundred nine” = 832,609

9. “fourteen thousand, two hundred ninety- one” = 14,291

10. “twenty-nine million, five hundred three thousand, seven hundred eighty-two” = 29,503,782

11. 10,000 = 10⁴

12. 100,000,000,000 = 10¹¹

13. 10⁷ = 10,000,000

14. 10¹² = 1,000,000,000,000

15. 10⁵ = 100,000

16. 59,400 = 5.94 x 10⁴

17. 23,000,000 = 2.3 x 10⁷

18. 5.8 x 10⁹ = 5,800,000,000

19. 2.492 x 10¹⁵ = 2,492,000,000,000,000

20. 1.2 x 10²³ = 1.2 x 10 x 10²² = 12 x 10²² > 9.8 x 10²²

21. 942 ≈ 900

22. 29,348 ≈ 30,000

23. 1,725,854 ≈ 1,700,000

24. 1,725,854 ≈ 1,726,000

25. 1,725,854 ≈ 2,000,000

Chapter 2

1. 48 + 86 = 134

2. 97 + 125 = 222

3. 638 + 842 = 1,480

4. 1,458 + 2,993 = 4,451

5. 12,477 + 8,394 = 29,871

6. 18 + 32 + 97 = 147

7. 91 + 74 + 139 = 304

8. 158 + 482 + 327 + 53 = 1,020

9. 71,864 + 34,745 + 9,326 = 115,935

10. 9,865 + 7,671 + 8,328 + 1,245 + 3,439 = 30,548

11. 596 - 312 = 284

12. 874 - 598 = 276

13. 1,058 - 897 = 161

14. 5,403 - 3,781 = 1,622

15. 14,672 - 5,839 = 8,833

16. 100 - 62 = 38

17. 250 - 183 = 67

18. 500 - 29 = 471

19. 400 - 285 = 115

20. 850 - 319 = 531

21. 462 x 53 = 24,486

22. 833 x 172 = 143,276

23. 1,005 x 53 = 53,265

24. 1,841 x 947 = 1,743,427

25. 2,864 x 563 = 1,612,432

26. 4,578 ÷ 42 = 109

27. 3,496 ÷ 19 = 184

28. 16,617 ÷ 29 = 573

29. 681 ÷ 14 = 48, remainder 9

30. 1,951 ÷ 35 = 55, remainder 26

Chapter 3

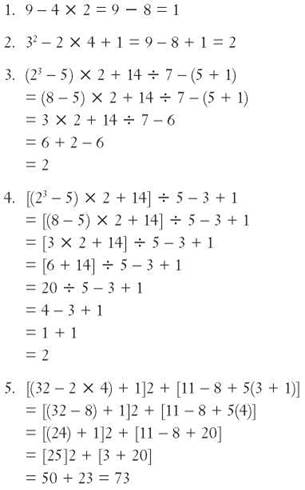
6. 2(35 + 14) = 70 + 28 = 98

7. 3(20 + 8) = 60 + 24 = 84

8. 7(100 - 2) = 700 - 14 = 686

9. 15(40 - 14) = 600 - 15 x 14 = 600 - (150 + 60) = 600 - 210 = 390

10. 250(1,000 - 400) = 250(600) = 150,000

11. |-19| = 19

12. |42| = 42

13. |0| = 0

14. |5 - 3| = |2| = 2

15. 7 + |5 - 3| = 7 + |2| = 9

16. -15 + 25 = 10

17. 19 + -12 = 7

18. -23 + 14 = -9

19. -58 + -22 = -80

20. 147 + -200 = -53

21. -17 - 4 = -17 + (-4) = -21

22. 39 - 24 = 39 + (-24) = 15

23. 26 - -12 = 26 + 12 = 38

24. -83 - 37 = -83 + (-37) = -120

25. -48 - -32 = -48 + 32 = -16

26. -4 X 30 = -120

27. 8 x -12 = -96

28. -7 x 15 = -105

29. -11 x -43 = 473

30. -250 x 401 = -100,250

31. 49 ÷ -7 = -7

32. -125 ÷ -15 = 8, remainder 5

33. -27 ÷ 9 = -3

34. 120 ÷ -6 = -20

35. -981 ÷ -9 = 109

Chapter 4

1. 51 is composite. 51 = 17 x 3

2. 91 is composite. 91 = 13 x 7

3. 173 is prime.

4. 229 is prime.

5. 5,229 is composite. 5,229 = 3 x 1,743 = 7 x 747 = 9 x 581 = 21 x 249 = 63 x 83

6. 78 = 2 x 3 x 13

7. 98 = 2 x 7 x 7

8. 189 = 3 x 3 x 3 x 7

9. 255 = 3 x 5 x 17

10. 512 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2

11. 20 0 = 2³ x 5²

12. 168 = 2³ x 3 x 7

13. 672 = 2⁵ x 3 x 7

14. 2,205 = 3² x 5 x 7²

15. 22,000 = 2⁴ x 5³ x 11

16. GCF of 18 and 42 is 6.

17. GCF of 42 and 70 is 14.

18. GCF of 144 and 242 is 2.

19. GCF of 630 and 945 is 315.

20. GCF of 286 and 715 is 143.

21. LCM of 14 and 35 is 70.

22. LCM of 45 and 105 is 315.

23. LCM of 286 and 715 is 1,430.

24. LCM of 21 and 20 is 420.

25. LCM of 88 and 66 is 264.

Chapter 5

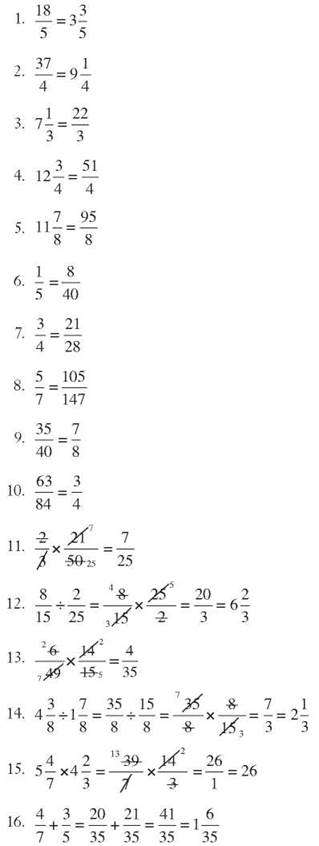
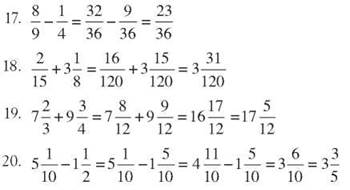
Chapter 6

1. 9.003 is nine and three thousandths.

2. 82.4109 is eighty-two and four thousand one hundred nine ten-thousandths.

3. “forty-two hundredths” is 0.42.

4. “forty-two ten-thousandths” is 0.0042.

5. “three hundred twelve and nine hundred one thousandths” is 312.901.

6. 0.00001 = 10^-5

7. 0.000000001 = 10^-9

8. 0.000000000000001 = 10^-15

9. 10^-6 = 0.000001

10. 10^-10 = 0.0000000001

11. 0.492 = 4.92 x 10^-1

12. 0.0000051 = 5.1 x 10^-6

13. 2.7 x 10^-5 = 0.000027

14. 8.19 x 10^-7 = 0.000000819

15. 5.302 x 10^-4 = 0.0005302

16. 45.9 + 19.75 = 65.65

17. 397.256 - 242.81 = 154.446

18. 17,401.12 + 15,293.101 = 32,694.221

19. 159.41006 - 143.0025 = 16.40756

20. 1.00027 + 0.4587332 = 1.4590032

21. 4.92 x 1.5 = 7.380 (or just 7.38)

22. 68.413 x 0.15 = 10.26195

23. 95.94 ÷ 7 7.8 = 12.3

24. 461.44 ÷ 7 1.12 = 412

25. 5,066.518 ÷ 7 8.6 = 589.13

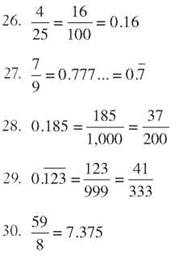
Chapter 7

1. 5x + 3x = 32

8x = 32

x = 4

5x = 20 3x = 12

There are 12 boys in Math Club.

2. 7x + 1x = 40

8x = 40

x = 5

7x = 35 1x = 5

There were 5 hybrids sold.

3. 2x + 3x = 20

5x = 20

x = 4

2x = 8 3x = 12

The florist should use 12 white roses and 8 red roses.

4. 4 x + 7x + 4 x = 45

15x = 45

x = 3

4 x = 12 7x = 21 4 x =12

There are 21 tigers.

5. 21x + 20x + 9x = 900

50x = 900

x = 18

21x = 378 20x = 360 9x = 162

There are 162 white balloons.

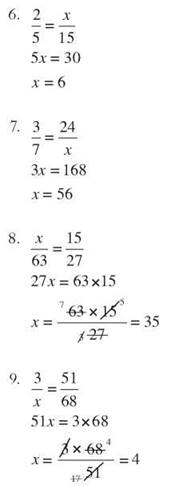
10.

5 x = 30

x = 6

11. 45 is 20% of 225.

20x = 4500

x = 225

12. 16 is 25% of 64.

64 x = 1600

x = 25

13. 15% of 80 is 12.

100x = 1200

x =12

14. 63 is 300% of 21.

21x =6300

x = 300

15. 120% of 55 is 66.

100x = 6600

x = 66

16.

17. 85.3% = 0.853

18.

19. 0.049 = 4.9%

20. 5.002 = 500.2%

21. I = prt

I = 18000 x 0.04x5 = $3,600

The interest is $3,600.

22. I = prt

130 = 1000 x r x 2

The interest rate is 6.5%.

23. tax= 0.047 x 175 = 8.225

You will pay $8.23 tax.

24. tip = 0.20 x $35.84 = 7.168

The tip should be approximately $7.17.

25. A total of 8 people at $22 per person is a bill of $176. The tip will be 0.18 x 176 = 31.68 or $31.68. Adding the tip to the bill brings the total to $207.68. Dividing that total eight ways means that each person’s share is $25.96.

26. The increase is $650 - $500 = $150.

500x = 15000

x = 30

The investment increased 30%.

27. The decrease is 7.5 - 6.75 = 0.75 minutes.

7.5x = 75

x = 10

Her time decreased 10%.

28. The change was an increase of 8.5 - 8 = 0.5 pounds.

8x = 50

x = 6.25

The dog’s weight increased 6.25%.

29. The decrease was 180 - 150 = 30 pounds.

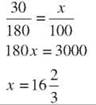
His weight decreased

30. The increase is 2 - 1.5 = 0.5 quarts.

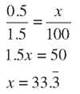
There was more ice cream.

Chapter 8

Chapter 9

1. 4x is a term.

2. -12 is a term.

3. -2t⁷ is a term.

4. 6/y is not a term.

5. a/6 is a term.

6. 7y² and 11y are unlike.

7. 3t² and 5t² are like.

8. 2x and 7x are like.

9. -9a² and -15a³ are unlike.

10. 132x³ and -83x³ are like.

11. -4x + 9x = 5x

12. 3a² - 2a³ is not possible.

13. 5xy + 6xy = 11 xy

14. 120xy² — 80xy² = 40xy²

15. 15z + 25x is not possible.

16. 6x(2x + 9) = 12x² + 54x

17. 12 + 5(x + 1) = 12 + 5x + 5 = 5x + 17

18. 6t²(t - 3) - 2? = 6t³ - 18t² - 2t² = 6t³ - 20t²

19. 5y(6y + 2) + 7y²(4 - 12y) = 30y² + 10y + 28y² - 84y³ = -84y³ + 58y² + 10y

20. 8a(2b - 5) - 2b(a - 2) = 16ab - 40a - 2ab + 4b = 14ab - 40a + 4b

21. -3a³ + 5a² - 3a + 12 is degree 3.

22. 6 + 3b — 4b is degree 2.

23. 2t - 9 + 7t² + 4t³ is degree 3.

24. 11y - 7y⁴ + 5y² - 3 is degree 4.

25. 6 - 4x² + 3x is degree 2.

26. a³ + 10a⁴ - 11a + 9 = 10a⁴ + a³- 11a + 9

27. 2b³ - 9b + 12b² - 5 = 2b³ + 12b² - 9b - 5

28. 3k⁴ + 8k⁵ - 13k - 7 = 8k⁵ + 3k⁴ - 13k - 7

29. 4 - 7m² + 14m⁴ + 2m³ = 14 m⁴ + 2m³ - 7m² + 4

30. 5p - 3 + 6p² - 15p³ = - 15p³ + 6p² + 5p - 3

Chapter 10

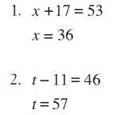
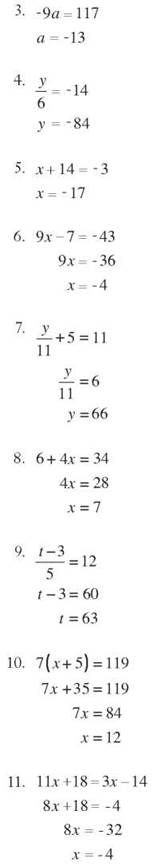
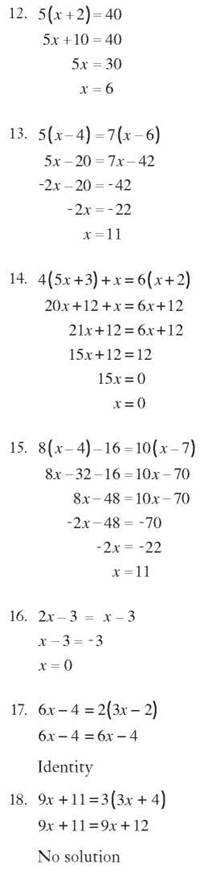
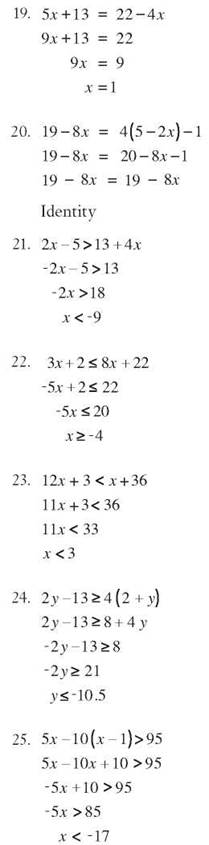
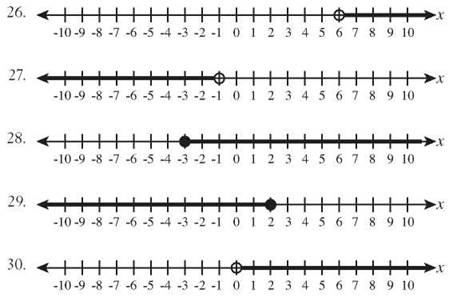
Chapter 11

Answers for questions 1 through 5 are shown on one graph below.

6. x + y = 7

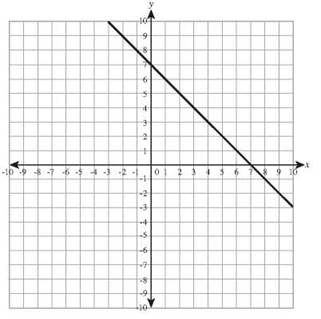
7. 2x - y = 3

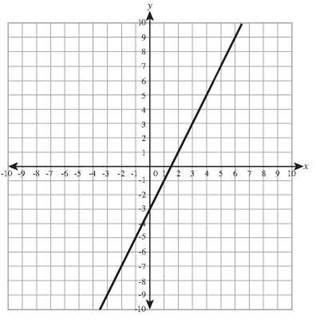
8. y = 3x - 6

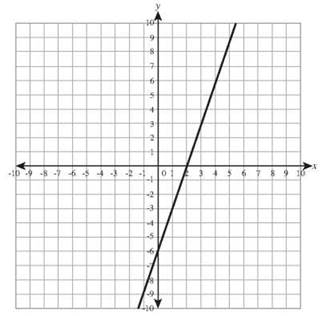
9. y = 8 - 2x

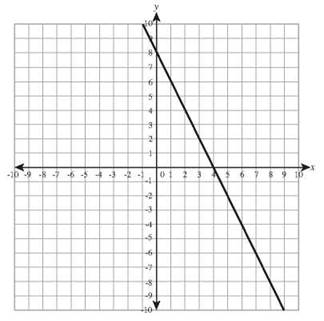
10.

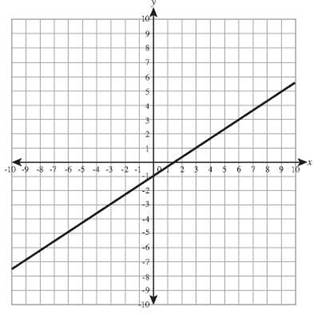
11. x + y = 10 has intercepts (0,10) and (10,0).

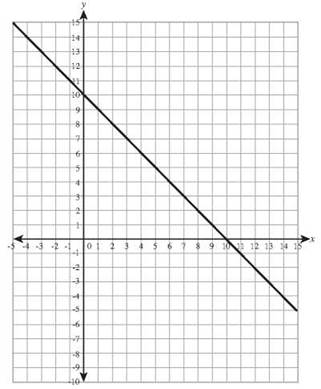
12. 6x + 2y =12 has intercepts (0,6) and (2,0).

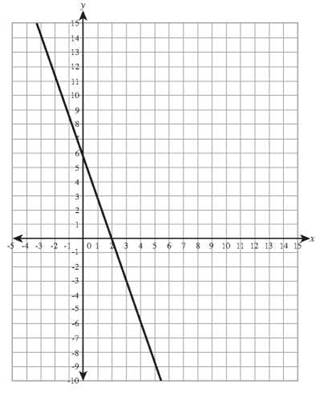
13. 2x- 3y = 9 has intercepts (0,-3) and (4.5,0).

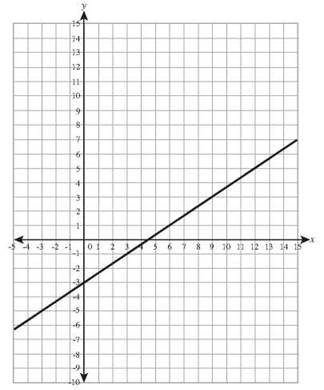
14. x -2y = 8 has intercepts (0,-4) and (8,0).

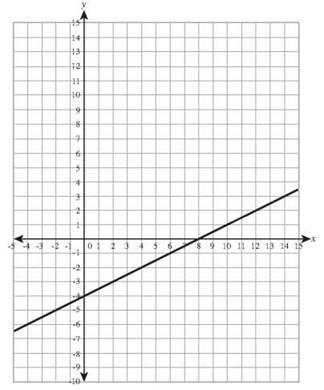
15. 6x + 2y =18 has intercepts (0,9) and (3,0).

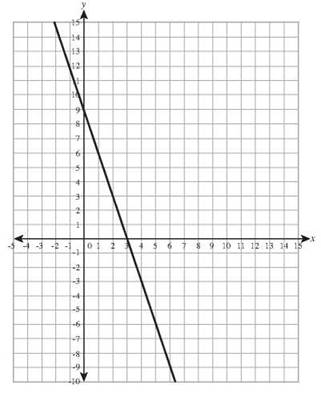
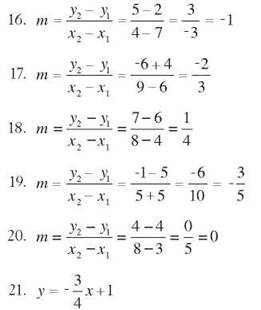
y-intercept: (0,1) slope: -3/4

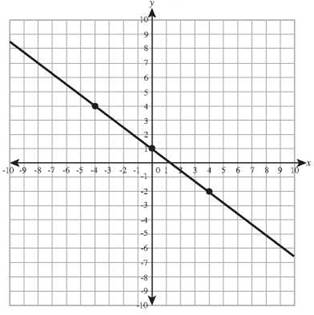
22. y = -4x + 6

y-intercept: (0,6) slope: -4

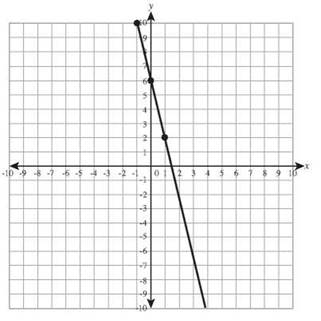
23. y = -3x - 4

y-intercept: (0,-4) slope: -3

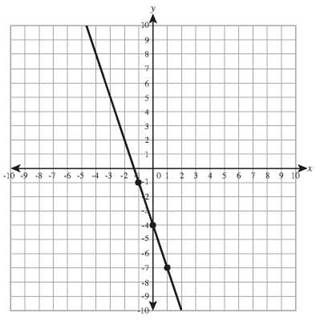
24. 2y = 5x - 6

y-intercept: (0,-3) slope: 5/2

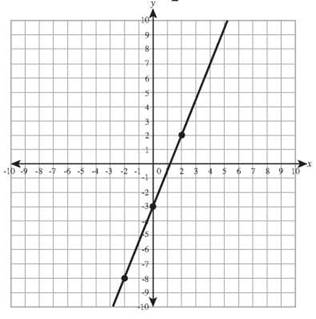
25. y — 6 = 3x +1

y-intercept: (0,7) slope: 3

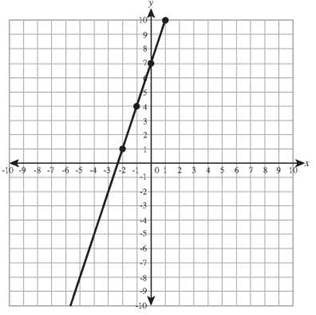
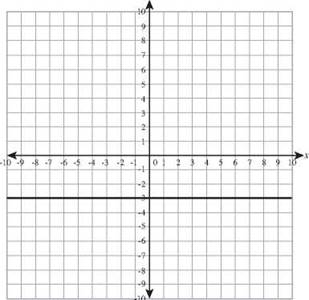
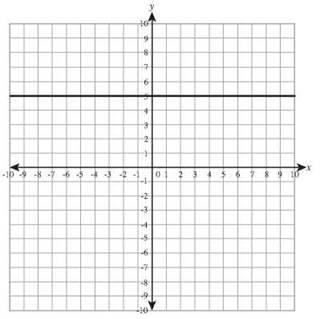
26. y = -3

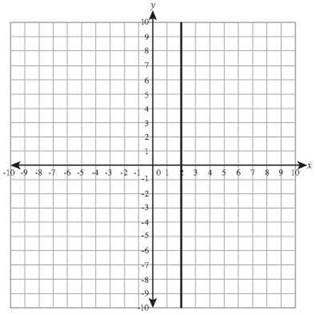
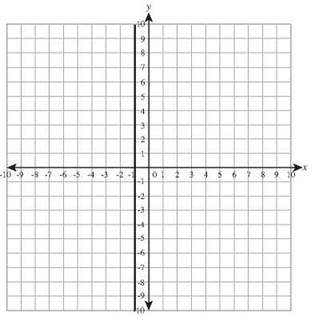
27. x = 2

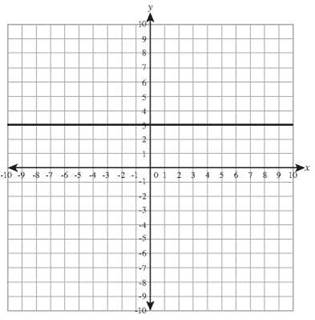
28. y = 5

29. x = -1

30. y + 1 = 4

31.

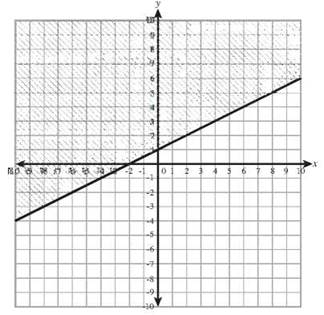
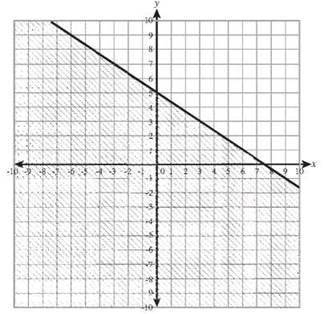
32. y ≤ 2x — 5

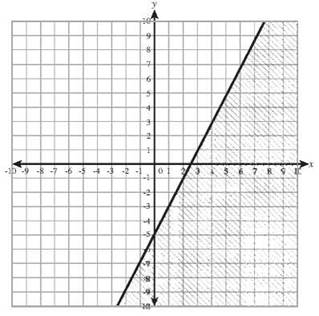
33. y > 5x — 4

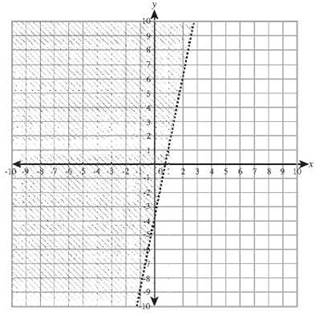
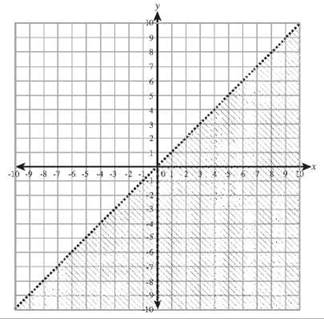
34. y < x

35.

Chapter 12

Sample answers are shown for questions 1-5.

Many answers are possible.

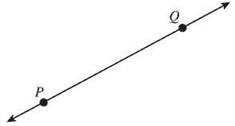
1. Line PQ

2. Ray YZ

3. Angle ∠DEF

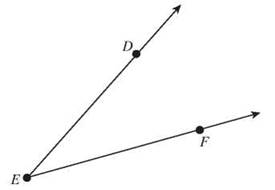
4. Rays AB and AC

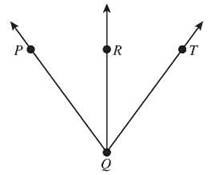
5. Angles ∠PQR and ∠RQT

6. If m∠X = 174°, then ∠X is a(n) obtuse angle.

7. If m∠T = 38°, then ∠T is a(n) acute angle.

8. If ∠X and ∠Y are supplementary, and m∠X = 174°, then m∠Y = 6°.

9. If ∠R and ∠T are complementary, and m∠T = 38°, then m∠R = 52°.

10. Lines and intersect at point Y. If m∠PYR = 51°, then m∠RYA = 129° and m∠TYA = 51°.

11. M is the midpoint of segment If PM = 3 cm, MQ= 3 cm and PQ= 6 cm.

12. H is the midpoint of If XY = 28 inches, then XH = 14 inches.

13. Ray bisects ∠CAT. If m∠CAT = 86°, then m∠HAT = 43°.

14. If m∠AXB = 27° and m∠BXC = 27°, then bisects ∠AXC.

15. m∠PYQ= 13°, m∠QYR = 12°, m∠RYS = 5°, and m∠SYT = 20°. True or False: bisects ∠PYT. m∠PYR = 13° + 12° = 25°. m∠RYT = 5° + 20° = 25°.

16. ∠PXY and ∠XYT are a pair of alternate interior angles.

17. ∠AXQ and ∠XYT are a pair of corresponding angles.

18. If m∠XYT = 68°, then m∠PXA = 112°.

19. If m∠PXY = 107°, then m∠RYB = 107°.

20. If then m∠XYR = 901.

21. Line a is parallel to line b. Both have slopes of -3.

22. is perpendicular to Slopes are negative reciprocals:

23. Line p and line q are neither parallel nor perpendicular.

24. Line and line are neither parallel nor perpendicular.

25. The line 3x - 2y = 12 has slope = 3/2 and the line 2x + 3y = 12 has slope = -2/3. The lines are perpendicular.

Chapter 13

1. m∠S = 180° - (48° + 102°) = 30°.

2. m∠TSQ = 48° + 102° = 150°.

3. m∠TSQ = 150°, m∠TRP = 132°, and m∠STN = 78°. The total of m∠TSQ + m∠TRP + m∠STN = 150° + 132° + 78° = 360°.

4. Placidville is 43 miles from Aurora, and Aurora is 37 miles from Lake Grove. The distance from Placidville to Lake Grove is greater than 6 miles and less than 80 miles.

5. Gretchen lives 5 miles from the library and 2 miles from school. The distance from the library to school is between 3 miles and 7 miles.

6. ∆RST is isosceles with RS = ST. If m∠SRT = 39°, then m∠STR = 39!.

7. In right triangle ∆ABC, m∠A = 90° - 19° = 71°.

8. False: If m∠P = 17° and m∠Q = 25°, m∠R = 180° - (17° + 25°) = 138°. ∆PQR is an obtuse triangle, not an acute triangle.

9. If m∠P = 17° and m∠Q= 25°, then the longest side of ∆PQR is side

10. If the vertex angle of an isosceles triangle measures 94°, then the base angles measure 43° each.

11. In ∆XYZ, If XY = 15 cm and YZ = 20 cm, XZ = 25 cm.

12. In ∆RST, If ST = 20 inches and RS = 52 inches, RT = 48 inches.

13. In ∆PQR, If PQ = PR = 3 feet, QR = 3√2 ≈ 4.24 feet.

14. In ∆CAT, If CT = 8 meters and CA = 4 meters, AT = 4√3 ≈ 6.93 meters.

15. In ∆DOG, If DO = 21 cm and DG = 35 cm, OG = 28 cm.

16. ∆ABC is a 30°-60°-90° right triangle, with hypotenuse 8 cm long. The length of the shorter leg is 4 cm.

17. ∆RST is an isosceles right triangle with legs 5 inches long. The length of the hypotenuse is 5√2 inches.

18. ∆ARM is a right triangle with AR = 14 meters, RM = 28 meters, and AM = 14√3 meters. m∠M = 30°.

19. ∆LEG is a right triangle with LE = EG and LG = 7√2 inches. m∠G = 45°.

20. ∆OWL is an isosceles right triangle with OW > OL. ∠L is the right angle.

21.

22.

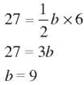
The base is 9 inches.

23. If the legs of the right triangle measure 20 cm and 48 cm, the hypotenuse is 52 cm. P = 20 + 48 + 52 = 120 cm.

24. In an equilateral triangle with a base b, the altitude will be and the area is If the area is 9√3 square inches, so and b = 6 inches. The perimeter is 18 inches.

25. The area of a right triangle with legs of 3 cm and 4 cm and hypotenuse of 5 cm is 6 square centimeters.

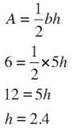
The altitude from the right angle to the hypotenuse is 2.4 centimeters long.

Chapter 14

1. In quadrilateral ABCD, and ABCD is a parallelogram because both pairs of opposite sides are parallel.

2. In quadrilateral PQRS, with diagonal ∠QRP ≅ ∠SPR and ∠QPR ≅ ∠SRP. PQRS is a parallelogram. The congruent alternate interior angles prove that both pairs of opposite sides are parallel.

3. In quadrilateral FORK, ∠F ≅ ∠K and FO = RK. There is sufficient information to say FORK is a parallelogram.

4. In quadrilateral LAMP, with diagonals and intersecting at S, ∆ALS ≅ ∆PMS and ∆AMS ≅ ∆PLS. The congruent triangles assure that both pairs of opposite sides are congruent, so LAMP is a parallelogram.

5. In quadrilateral ETRA, with diagonals and intersecting at X, TX = RX and EX = AX. There is not enough information to guarantee that ETRA is a parallelogram.

6. In quadrilateral FORT, and FORT is a rectangle.

7. In quadrilateral CAMP, CA = AM = MP = CP and CAMP is a square.

8. In quadrilateral VASE, diagonals and are congruent, but sides and are not. VASE is a rectangle.

9. In quadrilateral SOAP, and SOAP is a parallelogram.

10. In quadrilateral COLD, diagonals and are perpendicular bisectors of one another, but they are not congruent. COLD is a rhombus.

11. In trapezoid ABCD, and is a median. AC = 14 cm and BD = 30 cm. Median measures 22 cm.

12. In trapezoid FIVE, and m∠F = 59°. m∠I = 121°.

13. In trapezoid TEAR, and TE = AR. If ∠E = 107°, m∠A = 107°, and m∠R = 73°.

14. In trapezoid ZOID, m∠Z = 83° and m∠I = 97°. If ZO = 4 cm, ID = 4 cm, because ZOID is an isosceles trapezoid.

15. In trapezoid PQRT, and is a median. If MN = 17 inches and PT = 21 inches,

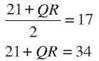
QR = 13 inches.

16. For a square with a side of 17 cm, perimeter is 68 cm and area is 289 cm².

17. For a rectangle 18 inches long and 9 inches wide, perimeter is 54 inches and area is 162 square inches.

18. For parallelogram ABCD, AB = CD = 7 inches, AC = BD = 21 inches, and the height from B perpendicular to and 3 inches, perimeter is 56 inches, and area is 63 square inches.

19. For a rhombus with sides 5 inches long and diagonals that measure 6 inches and 8 inches, perimeter is 20 inches and area is 5 square inches.

20. If the area of a parallelogram with a height of 48 cm is 3,600 square centimeters, the base to which that altitude is drawn (and the opposite side) must measure 75 cm. If the perimeter is 250 cm, the other two sides each measure 50 cm.

21. The number of diagonals in an octagon is

22. The total of the measures of all the interior angles in a nonagon is 180° (9- 2) = 1260°.

23. If a hexagon is regular, the total of the measures of all the interior angles is 180° (6 - 2) = 720°, and the measure of any one of its interior angles is

24. If the interior angles of a polygon add up to 900°, then 900° = 180°(n - 2), and n - 2 = 5. The polygon has 7 sides.

25. If a polygon has a total of 119 possible diagonals, so n(n-3) = 238. The factors of 238 are 2 x 119, 7 x 34, and 14 x 17. The last pair differ by 3, so n = 17.

26. The area of a regular pentagon with sides 8 cm long and an apothem 5 cm long is

27. The area of an octagon with a perimeter of 40 inches and an apothem of 5 inches is square inches.

28. The area of a regular decagon in which each of the 10 sides measure 2 meters and the apothem is 1.5 meters is square meters.

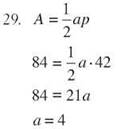
If the perimeter of a regular hexagon is 42 inches and its area is 84 square inches, its apothem is 4 inches.

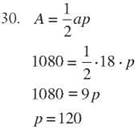
A regular pentagon with an area of 1,080 square inches and an apothem of 18 inches has a perimeter of 120 inches. Each side is 24 inches.

Chapter 15

1. An arc less than half a circle is a minor arc.

2. The distance from the center point to any point on the circle is called the radius.

3. Two circles with the same center are concentric circles.

4. If two circles touch each other at just one point, the circles are tangent.

5. An arc that is exactly half the circle is called a semicircle.

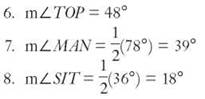
9. ∠ITS is inscribed in a semicircle. m∠ITS = 90°.

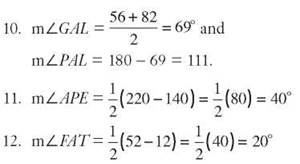
13. ∠RAC intercepts an arc of 360 - 72 = 288°.

14. Let x = the measure of arc

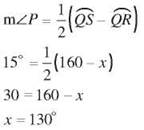
15. but 2x + x = 360, so x = 120 and m∠P = 60°.

16. The area of a circle with a radius of 9 cm is 81π cm².

17. The circumference of a circle with a diameter of 12 inches is 12π inches.

18. The area of a circle with a diameter of 32 cm is 16²π = 256π cm².

19. The radius of a circle with an area of 36π square meters is 6 meters, its diameter is 12 meters, and its circumference is 12π meters.

20. The diameter of a circle with a circumference of 24π feet is 24 feet, its radius is 12 feet, and its area is 144π square feet.

21. The equation of a circle with its center at the origin and a radius of 3 units is x² + y² = 9.

22.

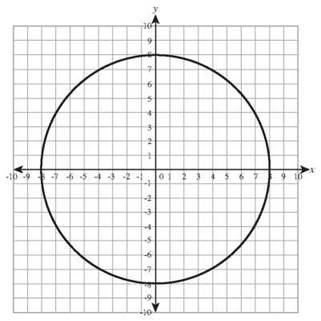
23. The center of the circle (x - 8)² + (x - 3)² = 49 is the point (8,3) and radius is 7.

24. The equation of a circle with center (4,9) and radius of 2 units is (x - 4)² + (y - 9)² = 4.

25.

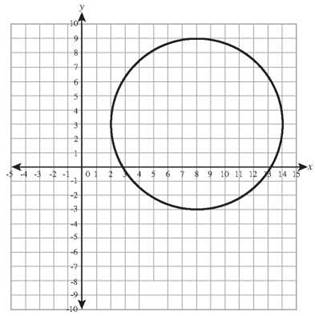
Circle of radius 6 centered at (8,3)

Chapter 16

1. SA = 2(15 x 24) + 2(15 x 10) + 2(24 x 10) = 1,500 cm²

2. SA = 2(1/2 x 5 x 12) + 5(8 + 12 + 13) = 225 square inches

3. SA = 2 x 65 + 42 x 30 = 1,390 cm²

4. SA = 2 x 387 + 5 x 15 x 4 = 1,074 square inches

5. SA = 6 x 17² = 1,734

6. V = 7³ = 343 cubic inches

7. V = 12 x 21 x 15 = 3,780 cm³

8. V = 1/2 x 3 x 4 x 6 = 36 cubic inches

9. V = 387 x 8 = 3,096 cubic inches

10. V = 65 x 50 = 3,250 cm³

11. SA = 4² + 1/2(16 x 5) = 16 + 40 = 56 square inches

12. SA = 62.4 + 1/2(36 x 10) = 62.4 + 180 = 242.4 cm²

13. SA = 172 + 1/2(50 x 18) = 172 + 450 = 622 cm²

14. SA = 260 + 1/2(60 x 10) = 260 + 300 = 560 square inches

15. SA = 10² + 1/2(40 x 13) = 100 + 260 = 360 square inches

16. If the slant height is 13 inches and half the side is 5 inches, the height is 12 inches. cubic inches.

17. If the slant height is 5 inches and half the side is 2 inches, the height is √21 ≈ 4.58 inches. cubic inches.

18. The base of the pyramid is an equilateral triangle with a side of 12 cm and an area of 62.4 square centimeters. The area is half the apothem times the perimeter, so and the apothem is a ~ 3.47. Use the Pythagorean Theorem with the apothem and slant height to find the height. a² + h² = l² becomes (3.47) + h² = 10² and h ≈ 9.38. The height is approximately 9.38, and cubic centimeters.

19. Use the area of the pentagon and its perimeter to find the apothem. so a ≈ 6.88. Use the Pythagorean Theorem to find the height. a² + h² = l² so (6.88)² + h² =(18)² and h ≈ 16.63. cubic centimeters.

20. The regular hexagon that forms the base has a perimeter of 60 inches and an area of 260 square inches, so use the formula to find the apothem. means that the apothem is inches long. Use the Pythagorean Theorem with the apothem and the slant height to find the height. a² + h² = l² so and h ≈ 4.99 inches. cubic inches.

21. h = 14 cm, r = 5 cm, SA = 2∙5²∙π + 2∙π∙5∙14 = 190π cm², V = π∙5²∙14 = 350π cm³.

22. h = 8 inches, d = 6 inches, r = 3 inches, SA = 2∙3²∙π + 2∙π∙3∙8 = 66π square inches, V = π∙3²∙8 = 72π cubic inches.

23. h = 2 m, C = 2π m, d = 2 m, r = 1 m, SA = 2∙1²∙π + 2∙π∙1∙2 = 6π m², V = π∙1²∙2 = 2π m³.

24. h = 82 cm, d = 90 cm, r = 45 cm, SA = 2∙45²∙π + 2∙π∙45∙82 = 11,430π cm², V = π∙45²∙82 = 166,050π cm³.

25. h = 20 inches, C = 20π inches, d = 20 inches, r = 10 inches, SA = 2∙10²∙π + 2∙π∙10∙20 = 600π square inches, V = π∙10²∙20 = 2,000π cubic inches.

26. r = 10 cm, h = 24 cm, l = 26 cm, SA = π∙10² + π∙10∙26 = 360π cm², V = 1/3∙π∙10²∙24 = 800π cm³

27. d = 8 inches, r = 4 inches, h = 3 inches, l = 5 inches, SA = π∙4¹ + π∙4∙5 = 36π square inches, V = 1/3∙π∙4²∙3 = 16π cubic inches

28. C = 16π cm, d = 16, r = 8, h = 6 cm, l = 10 cm, SA = π∙8² + π∙8∙10 = 144π cm², V = 1/3∙π∙8²∙6 = 128π cm³

29. r = 12 inches, h = 5 inches, l = 13, SA = π∙12² + π∙12∙13 = 300π square inches, V = 1/3∙π∙12²∙5 = 240π cubic inches

30. A = 324π cm, r = 18 cm, h = 24 cm, l = 30 cm, SA = π∙18² + π∙18∙30 = 864π cm², V = 1/3∙π∙18²∙24 = 2,592π cm³

31. r = 8 inches, SA = 4∙π∙8² = 256π square inches

32. r = 12 cm, V = 4/3∙π∙12³ = 2,304π cm³

33. d = 4 m , r = 2m, SA = 4∙π∙2² = 16π m²

34. d = 6 feet, r = 3 feet, V = 4/3∙π∙3³ = 36π cubic feet

35. V = 4500π cm³, r = 15 cm

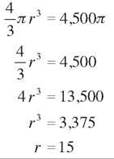
Chapter 17

1. Shaded area = area of large square - area of 2 white squares = 7² = 2∙3² = 49 - 18 = 31 square units.

2. Shaded area = area of rectangle - area of two white strips adjusted for overlap of white strips = 20 x 6 - (20 x 1 + 6 x 1 - 1 x 1) = 120 - 25 = 95.

3. Shaded area = Vi the area of large circle + 1/2 the area of small circle = 72π + 12.5π = 84.5π.

4. Shaded area = 1/2 x 1 x 12 = 6.

5. Flip one shaded section. Shaded area =

6. ∆ABC ≅ ∆XYZ by ASA

7. ∆ACT ≅ ∆IWN by AAS

8. ∆BIG and ∆MAN cannot be determined.

9. , ∆CAT ≅ ∆DOG by SSS

10. ∆BOX ≅ ∆CAR by SAS

11. ∆ABC~∆XYZ,

12. ∆RST~∆FED,

13. ∆PQR~∆VXW,

14. ∆MLN~∆LJK,

15. ∆ZXY~∆BCA,

16. ∆GHI~∆ARM, GH = 9 ft, GI = 8 ft, AR = 12 ft. Find AM.

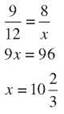
17. ∆JKL~∆DOG, JK = 17 m, JL = 25 m, DG = 30 m. Find DO.

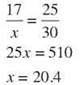
18. ∆ABC~∆XYZ, AB = 21 cm, BC = 54 cm, XY = 7 cm. Find YZ.

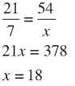
19. ∆DEF~∆CAT, DE = 65 in, EF = 45 in, CA = 13 in. Find AT.

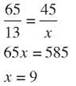
20. ∆MNO~∆LEG, MN = x - 3, NO EG = 21, LE = 2x + 4. Find LE.

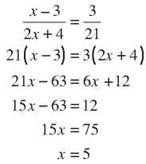
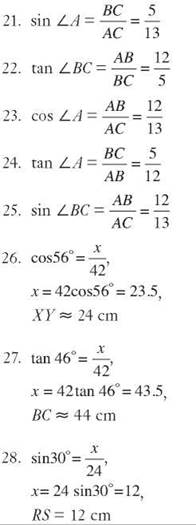
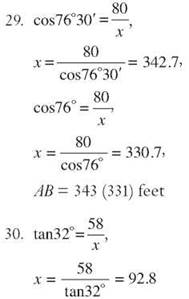
Side is 58 m. Find the length of to the nearest centimeter. XY ≈ 93.

Chapter 18

1. 2 x 4 = 8

2. 2 x 5 x 4 = 40

3. 2 x 5 x 3 x 4 = 120

4. 2 x 5 x 4 x 4 = 160

5. 2 x 5 x 4 x 3 x 2 x 4 = 960

6. 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720.

7. 7! = 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5,040.

8. 7! ÷ 6 = 840.

9. The permutations of 9 things taken 3 at a time = 504.

10. The permutations of 10 things taken 4 at a time = 5,040.

11. The number of combinations of 6 things taken 3 at a time = 20.

12. The number of combinations of 7 things taken 4 at a time = 35.

13. The number of combinations of 5 things taken 2 at a time = 10.

14. The number of different committees of 5 people that can be chosen from a group of 12 people is 792.

15. If you are going to choose 3 toppings from a list of 12 possibilities and the order in which you put toppings on does not matter, you have 220 sundaes to choose from.

16. The probability of drawing a heart and then a queen is

17. The probability of drawing a heart and then a heart is

18. The probability of drawing a black card and then a red card is

19. The probability of drawing a king and a queen is

20. The probability of drawing two black cards is

21. The probability that the marble chosen is red or blue is

22. The probability that the chosen marble is yellow or blue is

23. The probability that the marble is green or white is

24. The probability that the chosen marble is yellow or red is

25. The probability that the marble is red or orange is

Chapter 19

1.

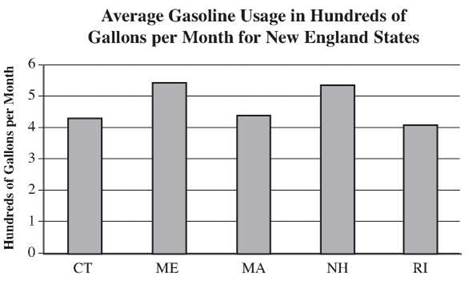
2. Rhode Island had the lowest average gasoline usage, possibly because the small size of the state means commuting distances are smaller.

3. Tacos outsell pasta by approximately 1,000 lunches.

4. Approximately 6,000 chicken lunches are sold per year.

5. Approximately 5,000 burgers are sold per year.

6.

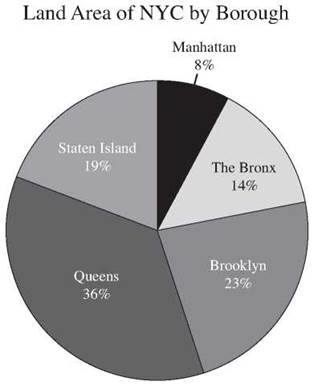
7. Area of Queens ÷ area of Manhattan = 109 ÷ 23 ≈ 4.7. Queens is between 4 and 5 times the size of Manhattan.

8. Percent of the enrollment in music courses = 4% + 22% + 16% = 42%.

9. Chorus had the largest enrollment.

10. Painting and Ceramics had the most similar enrollments.

11. Art History was 20% of enrollment, so 20% of 461 is approximately 92 students.

12.

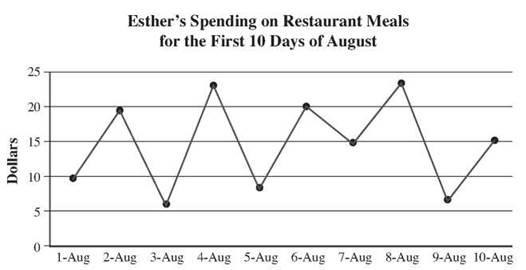
13. Esther’s restaurant spending alternates large and small expenditures.

14. Esther’s spending varied by only 25 cents on August 4^th and 8^th and on August 7^th and 10^th.

15. Sales have the greatest positive change from June to July.

16. Sales had the steepest drop from August to September.

17. November had sales most similar to the number of hot dogs sold in February.

Chapter 20

1. For data set A, mean = 3.1

2. For data set B, mean = 71.8

3. For data set C, mean = 5.3

4. For data set D, mean = 35

5. For data set E, mean = 3.2

6. The median of {2, 2, 2, 3, 3, 4, 4, 4, 4} is 3.

7. The median of {34, 54, 78, 92, 101} is 78.

8. The median of {3, 4, 5, 4, 7, 8, 9, 2, 10, 1} is 4.5.

9. The median of {32, 34, 36, 38} is 35.

10. The median of {2, 2, 3, 4, 5} is 3.

11. The mode of {2, 2, 2, 3, 3, 4, 4, 4, 4} is 4.

12. B = {34, 54, 78, 92, 101} has no mode.

13. The mode of {3, 4, 5, 4, 7, 8, 9, 2, 10, 1} is 4.

14. D = {32, 34, 36, 38} has no mode.

15. The mode of {2, 2, 3, 4, 5} is 2.

16. For data set A, Q1 = 4, Median = 8.5, Q3 = 32.

17. For data set B, Q1 = 3, Median = 4, Q3 = 66.

18. For data set C, Q1 = 25, Median = 64, Q3 = 83.

19. George’s placement at the 54^th percentile means that his score is slightly above the mean, but Harry’s 43^rd percentile places him below the mean. George did better.

20.

21. The range of {34, 54, 78, 92, 101} is 101 - 34 = 67.

22. The range of {3, 4, 5, 4, 7, 8, 9, 2, 10, 1} is 10 - 1 = 9.

23. The interquartile range of {3, 4, 5, 4, 7, 8, 9, 2, 10, 17, 32, 34, 36, 38} is 32 - 4 = 28.

24. The IQR of {2, 2, 2, 3, 3, 4, 4, 4, 4, 34, 54, 78, 92, 101} is 54 - 3 = 51.

25. The standard deviation of the test scores {69, 70, 73, 74, and 74} is approximately 2.345.