Mathematics for the liberal arts (2013)
Part I. MATHEMATICS IN HISTORY
Chapter 2. THE GROWTH OF MATHEMATICS TO 1600
2.3 Islam
The Big Dipper in the sky has eight stars: Alkaid, Mizar and Alcor (a famous double star), Alioth, Megrez, Phecda, Merak, and Dubhe. These names have something in common: they are Arabic. Many of our star names are Arabic. This is because Europe learned its science from the Muslims. In the centuries around the year 1000 CE, the Muslims were the greatest scientists in the world. They had translated and studied the ancient Greek texts, and adopted the superior Indian decimal system. They had learned astronomy from Greek, Mesopotamian, and Indian sources. They eventually taught all of these to Europe, but not until they had added considerably to this inherited tradition.
History to 1600: An Overview
Muslim history.

Muhammad (570–632) lived in the Arabian desert in what is now Saudi Arabia, where he founded a new religion called Islam, Arabic for “submission to God.” Within twenty years of the prophet Muhammad’s death, the armies of Islam had conquered Syria, Mesopotamia, Persia, Egypt, and Libya.
The political successors of Muhammad were called caliphs (from the Arabic khalifah, “successor”). In the middle of the 7th century, there was a struggle over who would be the next caliph. Eventually, the Umayyad clan emerged as the victors, establishing the Umayyad caliphate, or dynasty, which lasted 661–750. This succession battle produced the major schism in Islam, with the minority Shi’a Muslims supporting a different caliph from the majority Sunni Muslims.
The Umayyad caliphate moved their capital from Saudi Arabia to Damascus, in Syria, where they used the old Persian and Roman bureaucracies. In the late 7th and early 8th centuries, after the internal politics were settled, Islam expanded once more, through northern Africa into Spain in the west, and as far as the Indus valley in the east.
The Umayyad dynasty was overthrown by the Abbasid family, except in the west, where the Umayyads retained their power for several more centuries, centered in Cordoba, Spain. The Abbasids, descendants of an uncle of Muhammad, established the Abbasid dynasty (750–1258). In 762 they moved their capital to the newly-founded city of Baghdad in modern-day Iraq, not far from where previous capital cities had served long-gone Mesopotamian states.
The following centuries were the golden age of Muslim culture. For a while, Baghdad was one of the largest, richest, and most civilized places in the world. Its scholars drew upon the preceding cultures of Mesopotamia, Persia, Greece, and India. Paper making was learned from the Chinese. Arabic became the lingua franca of science. Mathematics flourished.
The Abbasids gradually lost power. Other dynasties arose, some of them centered further east, particularly in Persia, modern-day Iran. In the 11th century, the Seljuk Turks established an empire that ruled lands from Egypt to India. In the 13th century, Mongol invaders conquered much of this area. Throughout this period Islamic mathematics continued, although at a gradually decreasing level.
The last great Islamic empire was that of the Ottomans (1326–1920), who eventually ruled much of Northern Africa, the Middle East, and Southeastern Europe, finally expiring in World War I. In 1453, after a long struggle, the Ottomans succeeded in conquering Constantinople, making it their capital. The empire’s most famous figure was Suleiman the Magnificent, who was sultan in 1520–1566.
During the period 1000–1500, Islam continued expanding south and east. Muslims converted much of Sub-Saharan Africa. Their merchants and missionaries also spread the faith to southeast Asia, as far as the Philippines. The most populous Muslim country today is Indonesia.
In the following pages, we trace the main accomplishments of the Islamic mathematics of this time. This history is hardly complete; there are still many manuscripts from a number of cultural centers that historians have not studied, and some that haven’t even been read.
Transmission
Scholars move more than most people. Major centers of learning usually are populated with many immigrants. Very few of the top philosophers of 4th century Athens were actually bom in Athens. A sizable percentage of American winners of Nobel science prizes emigrated from other countries.
When Alexandria became inhospitable to learning, some of its scholars, particularly Nestorian Christians, moved to Syria. Late in the 5th century, they had to move again, this time to Persia, where they were joined after 529 by others from newly-intolerant Greece. The major center was at Jundishapur in modern-day southwestern Iran, which flourished in the 6th and 7th centuries, known especially for its medicine.
Around 800 the intellectual center of western Asia moved to Baghdad. An important person in this development was the caliph Har![]() n al-Rash
n al-Rash![]() d,1 who ruled 786–809. His caliphate, and that of his son al-Ma‘m
d,1 who ruled 786–809. His caliphate, and that of his son al-Ma‘m![]() m (r. 813–33), was a golden age for learning. The court of al-Rash
m (r. 813–33), was a golden age for learning. The court of al-Rash![]() d was immortalized in The Thousand and One Nights. The Almanon crater on the Moon is named for al-Ma‘m
d was immortalized in The Thousand and One Nights. The Almanon crater on the Moon is named for al-Ma‘m![]() m, in recognition of his support for astronomy. These rulers were eager to learn from other cultures and welcomed scholars who were not necessarily Muslims. Tolerance was not carried to extremes, however; later in his life, al-Ma‘m
m, in recognition of his support for astronomy. These rulers were eager to learn from other cultures and welcomed scholars who were not necessarily Muslims. Tolerance was not carried to extremes, however; later in his life, al-Ma‘m![]() m established an inquisition to enforce, through torture and execution, his enlightened philosophy.
m established an inquisition to enforce, through torture and execution, his enlightened philosophy.
Starting in the late 8th century, many scientific classics were translated into Arabic, the first being Indian astronomical texts. Har![]() n al-Rash
n al-Rash![]() d established a library in Baghdad, collecting manuscripts from throughout the region. Delegations were sent by al-Ma‘m
d established a library in Baghdad, collecting manuscripts from throughout the region. Delegations were sent by al-Ma‘m![]() m to Syria, Constantinople, and Syracuse in search of Greek writings. Euclid was translated in the year 800, followed by works of Archimedes, Apollonius, Ptolemy, Diophantus, and others, including major medical and philosophical texts. By the end of the 9th century, most of the major works had been translated. In fact, many of the classic Greek texts are available to us today only in Arabic translations.
m to Syria, Constantinople, and Syracuse in search of Greek writings. Euclid was translated in the year 800, followed by works of Archimedes, Apollonius, Ptolemy, Diophantus, and others, including major medical and philosophical texts. By the end of the 9th century, most of the major works had been translated. In fact, many of the classic Greek texts are available to us today only in Arabic translations.
In 830 al-Ma‘m![]() m established a research institution called Bayt al-Hikmah (The House of Wisdom). With its associated library and astronomical observatory, it became a major center of Islamic scholarship. Many of the translations mentioned above were done here, but also original research in the sciences, including mathematics.
m established a research institution called Bayt al-Hikmah (The House of Wisdom). With its associated library and astronomical observatory, it became a major center of Islamic scholarship. Many of the translations mentioned above were done here, but also original research in the sciences, including mathematics.
In the 10th century, Baghdad began declining, and much of the subsequent mathematics moved farther east. Major centers were established at various times in Nishapur and Isfahan in Iran, in Samarkand in Uzbekistan, and other places. Farther west, Cairo hosted important scholars, and work was done in Damascus, Syria, in Cordoba, Seville, and Toledo in Islamic Spain, and in the Maghreb of northern Africa.
Numeration
Muslim mathematicians.
The Hindu system of numbers developed gradually into the Hindu-Arabic system—the system we use—over a number of centuries. The Hindu system, a decimal place-value system with a zero but no decimal fractions, was known in western Asia as early as 662, when it/was described in a Syrian text by the Nestorian bishop Severus Sebokht. (By decimal fraction we mean, for example, .2 instead of 1/5.) The Arabs at this time had a number of systems. Merchants used a form of finger reckoning. There was also a system that represented numbers using letters. Astronomers were familiar with the Babylonian sexagesimal place-value system.
The earliest known Arabic text on the Hindu system is the Kit![]() b al-jam‘waltafr
b al-jam‘waltafr![]() q bi h
q bi h![]() sab al-Hind (Book on Addition and Subtraction after the Method of the Indians), by Muhammad al-Khw
sab al-Hind (Book on Addition and Subtraction after the Method of the Indians), by Muhammad al-Khw![]() rizm
rizm![]() . The original Arabic text has been lost, but is available in Latin versions made in the 12th century. In this book, al-Khw
. The original Arabic text has been lost, but is available in Latin versions made in the 12th century. In this book, al-Khw![]() rizm
rizm![]() explained how to write numbers using the nine digits plus zero, and also how to add, subtract, multiply, divide, and extract square roots. This is an elementary, practical book, emphasizing the value of the new system in writing large numbers and in doing calculations. The calculations are for the dust board, a flat surface on which sand was spread.
explained how to write numbers using the nine digits plus zero, and also how to add, subtract, multiply, divide, and extract square roots. This is an elementary, practical book, emphasizing the value of the new system in writing large numbers and in doing calculations. The calculations are for the dust board, a flat surface on which sand was spread.
![]() ibn
ibn ![]() (c. 780–850)
(c. 780–850)
It is not known where al-Khw![]() rizm
rizm![]() was bom. Given his name, he or his ancestors may have came from Khw
was bom. Given his name, he or his ancestors may have came from Khw![]() rizm, a region in what is now Uzbekistan and Turkmenistan. It is known that he worked in Baghdad and was one of the first scholars at the House of Wisdom.
rizm, a region in what is now Uzbekistan and Turkmenistan. It is known that he worked in Baghdad and was one of the first scholars at the House of Wisdom.
In addition to his work on mathematics, al-Khw![]() rizm
rizm![]() published on geography, and reportedly was called upon to cast a horoscope for the caliph al-Wath
published on geography, and reportedly was called upon to cast a horoscope for the caliph al-Wath![]() q in 847. He prudently predicted another 50 years for the caliph, who died 10 days later.
q in 847. He prudently predicted another 50 years for the caliph, who died 10 days later.
![]()
Hindu arithmetic was gradually adopted in Arabic scientific circles. The earliest arithmetic text which still survives in Arabic is the Kit![]() b al-fu
b al-fu![]()
![]() l fi-l-
l fi-l-![]() is
is![]() b al-hind
b al-hind![]() (The Book of Chapters on Hindu Arithmetic), written about 952 by Abu 1-Hasan al-Uql
(The Book of Chapters on Hindu Arithmetic), written about 952 by Abu 1-Hasan al-Uql![]() d
d![]() s
s![]() . This has the first recorded use of decimal fractions. Al-Uql
. This has the first recorded use of decimal fractions. Al-Uql![]() d
d![]() s
s![]() showed how to divide by 10 (move the number one place to the right) and by 2 (move to the right and multiply by 5). The Hindus did not use decimal fractions, so this was an invention of the Arabs, who had the Babylonian sexagesimal fractions as a model. Al-Uql
showed how to divide by 10 (move the number one place to the right) and by 2 (move to the right and multiply by 5). The Hindus did not use decimal fractions, so this was an invention of the Arabs, who had the Babylonian sexagesimal fractions as a model. Al-Uql![]() d
d![]() s
s![]() also made a pitch to replace the dust board by paper.
also made a pitch to replace the dust board by paper.
Abu ![]() (c. 920–980)
(c. 920–980)
Little is known of Al-Uql![]() d
d![]() s
s![]() . We do know that he wrote at least two works, and composed The Book of Chapters on Hindu Arithmetic in Damascus. He claimed to have traveled widely, and may have worked in Baghdad.
. We do know that he wrote at least two works, and composed The Book of Chapters on Hindu Arithmetic in Damascus. He claimed to have traveled widely, and may have worked in Baghdad.
The al-Uql![]() d
d![]() s
s![]() part of his name came from “Euclid.” He apparently earned his living by making and selling copies of Euclid’s Elements.
part of his name came from “Euclid.” He apparently earned his living by making and selling copies of Euclid’s Elements.
![]()
There is some question about how thoroughly al-Uql![]() d
d![]() s
s![]() understood decimal fractions, since he gave only limited examples. The first text that displays an unambiguously thorough understanding is the al-Qiw
understood decimal fractions, since he gave only limited examples. The first text that displays an unambiguously thorough understanding is the al-Qiw![]() m
m![]() f
f![]() al-
al-![]() is
is![]() b al-
b al-![]() ind
ind![]() (Treatise on Arithmetic) of 1172, by Ibn Ya
(Treatise on Arithmetic) of 1172, by Ibn Ya![]() y
y![]() al-Maghrib
al-Maghrib![]() al-Samaw’al (biography in the next section). In particular, he understood that, in the case where the decimal fraction could not be exact, e.g., dividing 210 by 13, we could get decimal fractions that approximate the answer as closely as desired. We now would write 210/13 = 16.153846….
al-Samaw’al (biography in the next section). In particular, he understood that, in the case where the decimal fraction could not be exact, e.g., dividing 210 by 13, we could get decimal fractions that approximate the answer as closely as desired. We now would write 210/13 = 16.153846….
Finally, we mention the Muftah al-![]() is
is![]() b (Key to Arithmetic), written in the 15th century by the Persian Ghiy
b (Key to Arithmetic), written in the 15th century by the Persian Ghiy![]() th al-D
th al-D![]() n Jamsh
n Jamsh![]() d al-K
d al-K![]() sh
sh![]() (biography in the section on trigonometry). This work introduced a better notation, a vertical line to separate the integer part and the decimal part of a number, e.g., 210/13 = 16|153846. …
(biography in the section on trigonometry). This work introduced a better notation, a vertical line to separate the integer part and the decimal part of a number, e.g., 210/13 = 16|153846. …
Our debt to the Islamic world for this number system is enshrined in our language. The word for zero in Arabic is sifr, meaning “empty,” which gave us our words “zero” and “cipher,” an old-fashioned word for zero. The name al-Khw![]() rizm
rizm![]() is also the origin for our word “algorithm,” a well-defined method of solving a problem. An example of an algorithm is long division.
is also the origin for our word “algorithm,” a well-defined method of solving a problem. An example of an algorithm is long division.
Algebra
Around 825 al-Khw![]() rizm
rizm![]() wrote a book on algebra, Al-kit
wrote a book on algebra, Al-kit![]() b al-mu
b al-mu![]() ta
ta![]() ar fi hisab al-jabr wa-l-muq
ar fi hisab al-jabr wa-l-muq![]() bala (The Condensed Book on the Calculation by Restoring and Comparing). The word al-jabr refers to the algebraic process of moving a negative quantity on one side of an equation to the other, where it becomes positive, e.g., replacing the equation 2x + 7 = 8 — x by 3x + 7 = 8. The word al-muqabala refers to the process of subtracting a number from both sides of the equation, e.g., replacing 3x + 7 = 8 by 3x = 1.
bala (The Condensed Book on the Calculation by Restoring and Comparing). The word al-jabr refers to the algebraic process of moving a negative quantity on one side of an equation to the other, where it becomes positive, e.g., replacing the equation 2x + 7 = 8 — x by 3x + 7 = 8. The word al-muqabala refers to the process of subtracting a number from both sides of the equation, e.g., replacing 3x + 7 = 8 by 3x = 1.
In this work al-Khw![]() rizm
rizm![]() explained how to solve linear and quadratic equations. He classified these equations into six types. He did not allow negative numbers, so for example he considered the equations 2x2 + 3x = 4 and 5x2 + 6 = 7x to be of different types. Nowadays, we would consider them both instances of ax2 + bx + c = 0, where any of a, b, or c can be negative. Although al-Khw
explained how to solve linear and quadratic equations. He classified these equations into six types. He did not allow negative numbers, so for example he considered the equations 2x2 + 3x = 4 and 5x2 + 6 = 7x to be of different types. Nowadays, we would consider them both instances of ax2 + bx + c = 0, where any of a, b, or c can be negative. Although al-Khw![]() rizm
rizm![]() did not allow negative solutions, he did, unlike many previous mathematicians, recognize that some quadratic equations had two solutions.
did not allow negative solutions, he did, unlike many previous mathematicians, recognize that some quadratic equations had two solutions.
All problems were stated in words; there was nothing like our modem notation. Here is one problem he solved. “What must be the square which, when increased by ten of its own roots, amounts to 39?” We would write this as: Solve x2 + 10x = 39 for x. Here is al-Khw![]() rizm
rizm![]() ’s solution.
’s solution.
The solution is this: You halve the number of roots, which in this case gives five. This you multiply by itself, the product is twenty-five. Add this to thirty-nine, the sum is sixty-four. Now take the root of this, which is eight, and subtract from it half the number of roots, which is five, the remainder is three. This is the root of the square you sought for, and the square itself is nine.
Translated, this is ![]() , which works out to x = 3.
, which works out to x = 3.
al-Khw![]() rizm
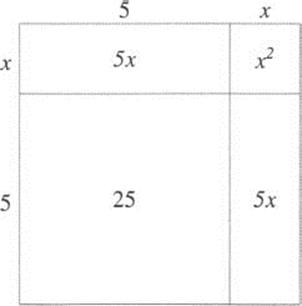
rizm![]() viewed his book as more practical than theoretical, but did include some proofs. Under the influence of the Greeks, at this time all proofs were geometric. To explain his solution above, he used a diagram like Figure 2.14. Note that the area of the larger square is x2 + 5x + 5x + 25 = (x2 + 10x) + 25 = 39 + 25 = 64. Since the area is also (x + 5)2, we have (x + 5)2 = 64, or x + 5 = 8, hence x = 3.
viewed his book as more practical than theoretical, but did include some proofs. Under the influence of the Greeks, at this time all proofs were geometric. To explain his solution above, he used a diagram like Figure 2.14. Note that the area of the larger square is x2 + 5x + 5x + 25 = (x2 + 10x) + 25 = 39 + 25 = 64. Since the area is also (x + 5)2, we have (x + 5)2 = 64, or x + 5 = 8, hence x = 3.
This text was very influential in Europe after it was translated in the 12th century. The word al-jabr was not translated, and eventually morphed into the word algebra.
One of the important developments in Islamic mathematics was the gradual “arith- metization” of algebra, treating algebraic problems as being about numbers, not tied to geometry. Recall the Greek notion of magnitude. In the equation x2 + 10x = 39, for example, x2 would be considered a different type of magnitude than x, since x2 represents an area and x a line segment. But by the time of the Egyptian mathematician Abu Kamil, that distinction was being eroded. Both expressions were often treated the same; they were just numbers.
Figure 2.14 Solving x2 + 10x = 39.
Ab![]() K
K![]() mil ibn Aslam (c. 850–930)
mil ibn Aslam (c. 850–930)
We know little of the life of Ab![]() K
K![]() mil. He lived in Egypt, and was influenced by the works of Euclid, Heron, and al-Khw
mil. He lived in Egypt, and was influenced by the works of Euclid, Heron, and al-Khw![]() rizm
rizm![]() , although he was too young to have met the latter.
, although he was too young to have met the latter.
Ab![]() K
K![]() mil wrote a number of mathematical books, including several which did not survive.
mil wrote a number of mathematical books, including several which did not survive.
![]()
In Kit![]() b f
b f![]() al-jabr wa’l-muq
al-jabr wa’l-muq![]() bala (variously translated as Algebra or Book on Algebra), Ab
bala (variously translated as Algebra or Book on Algebra), Ab![]() K
K![]() mil treated more complicated problems than had al-Khw
mil treated more complicated problems than had al-Khw![]() rizm
rizm![]() . In particular, he was at ease with expressions involving irrational roots, surds. In one of his problems, a solution was
. In particular, he was at ease with expressions involving irrational roots, surds. In one of his problems, a solution was ![]() (which he expressed in words).
(which he expressed in words).
Ab![]() K
K![]() mil also used the technique of substitution to reduce a problem to an easier one. In one example, he treats the equation
mil also used the technique of substitution to reduce a problem to an easier one. In one example, he treats the equation
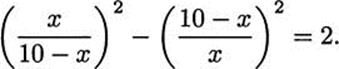
First he substitutes for ![]() . Let us call it y; then 1/y2 – y2 = 2. Multiplying by y2, we get 1 – y4 = 2y2. Now we can substitute z = y2 to get 1 – z2 = 2z. Since this is a familiar quadratic, we can solve for z, then y, then x. Details are left to the exercises.
. Let us call it y; then 1/y2 – y2 = 2. Multiplying by y2, we get 1 – y4 = 2y2. Now we can substitute z = y2 to get 1 – z2 = 2z. Since this is a familiar quadratic, we can solve for z, then y, then x. Details are left to the exercises.
The next major developer of Islamic algebra was Ab![]() Bakr al-Karaj
Bakr al-Karaj![]() . In al-Fakhri (The Marvelous), al-Karaj
. In al-Fakhri (The Marvelous), al-Karaj![]() introduced some of the algebra of polynomials. In particular, he wrote in a general way about higher powers, what we would write as x, x2, x3, …, and their reciprocals,
introduced some of the algebra of polynomials. In particular, he wrote in a general way about higher powers, what we would write as x, x2, x3, …, and their reciprocals, ![]() He developed rules for adding, subtracting, and multiplying polynomials, although the only division.he recognized was by monomials (polynomials with only one term, e.g., 2x3).
He developed rules for adding, subtracting, and multiplying polynomials, although the only division.he recognized was by monomials (polynomials with only one term, e.g., 2x3).
Ab![]() Bakr al-Karaj
Bakr al-Karaj![]() (c. 980–1030)
(c. 980–1030)
It is uncertain where al-Karaj![]() was bom. The most popular view among historians is that he was Persian, but some place his birth near Baghdad. What is certain is that he worked in Baghdad in the early 11th century. He wrote a number of works on mathematics and engineering,
was bom. The most popular view among historians is that he was Persian, but some place his birth near Baghdad. What is certain is that he worked in Baghdad in the early 11th century. He wrote a number of works on mathematics and engineering,
![]()
Al-Karaj![]() also studied irrational numbers. He produced a number of results such as the following.
also studied irrational numbers. He produced a number of results such as the following.
![]()
Ibn Ya![]() y
y![]() al-Maghrib
al-Maghrib![]() al-Samaw’al extended al-Karaj
al-Samaw’al extended al-Karaj![]() ’s algebra of polynomials. He took the important step of allowing negative coefficients. He also provided charts for doing operations on polynomials, apparently based on the dust board. These charts, reminiscent of Chinese counting boards, made complicated computations easier. In them, he represented each term of an extended polynomial, which could include negative powers of x, by a column. In a somewhat simplified example, the chart below would represent the expression 2x3 – 4x2 + 1 – 8x–1 + x–2.
’s algebra of polynomials. He took the important step of allowing negative coefficients. He also provided charts for doing operations on polynomials, apparently based on the dust board. These charts, reminiscent of Chinese counting boards, made complicated computations easier. In them, he represented each term of an extended polynomial, which could include negative powers of x, by a column. In a somewhat simplified example, the chart below would represent the expression 2x3 – 4x2 + 1 – 8x–1 + x–2.
![]()
Al-Samaw’al explained how to add, subtract, multiply, and divide such expressions. In particular, he discovered long division. You may recall that al-Samaw’al was also the first to completely master decimal fractions. This is intimately related to his work in algebra, for a decimal number may be thought of as a type of extended polynomial with the unknown being 10. For example, if we let x = 10 in the expression 7x2 + 8x + 2 + 3x–1 + 8x–2, we get the number 782.38.
Ibn Ya![]() y
y![]() al-Maghrib
al-Maghrib![]() al-Samaw’al (1125–1174)
al-Samaw’al (1125–1174)
Al-Samaw’al was bom in Baghdad, the son of a Jewish scholar from Morocco. At the time he grew up, Baghdad was no longer a cultural hotbed, and he was required to learn mathematics on his own.
Al-Samaw’al reportedly wrote 85 works, few of which survive. His major mathematical work, Al-B![]() hir fi’l-his
hir fi’l-his![]() b (The Shining Book of Calculation) was written when he was nineteen. Later, he traveled extensively and was a famous physician. The only one of his medical texts to survive is The Companion’s Promenade in the Garden of Love, basically a sex manual.
b (The Shining Book of Calculation) was written when he was nineteen. Later, he traveled extensively and was a famous physician. The only one of his medical texts to survive is The Companion’s Promenade in the Garden of Love, basically a sex manual.
When al-Samaw’al was about forty years old, he converted to Islam, writing a famous book that has since been used as a Muslim polemic against Judaism.
![]()
With the works of al-Karaj![]() and al-Samaw’al and their predecessors, algebra was freed from geometry. For al-Karaj
and al-Samaw’al and their predecessors, algebra was freed from geometry. For al-Karaj![]() , the goal of algebra is the “determination of unknowns starting from known premises.” Al-Samaw’al clearly understood the intimate connections between algebraic and arithmetic manipulations.
, the goal of algebra is the “determination of unknowns starting from known premises.” Al-Samaw’al clearly understood the intimate connections between algebraic and arithmetic manipulations.
Another theme in Islamic algebra was the study of cubic equations, ones of the form ax3 + bx2 + cx + d = 0, where a, b, c, and d are given numbers. The problem is to find all values of x for which the equation holds. A leading figure in this study was ‘Umar ibn Ibr![]() h
h![]() m al-Khayy
m al-Khayy![]() m
m![]() .
.
‘Umar ibn Ibr![]() h
h![]() m al-Khayy
m al-Khayy![]() m
m![]() (Omar Kayyam) (1048–1131)
(Omar Kayyam) (1048–1131)
The Persian scholar ‘Umar ibn Ibr![]() h
h![]() m al-Khayy
m al-Khayy![]() m
m![]() was bom in Nishapur, a major cultural center of that time, located in modern-day northeastern Iran. His family’s background may be indicated by his name; in Arabic, al-kayy
was bom in Nishapur, a major cultural center of that time, located in modern-day northeastern Iran. His family’s background may be indicated by his name; in Arabic, al-kayy![]() m
m![]() means “the tentmaker.”
means “the tentmaker.”
Al-Khayy![]() m
m![]() spent his working life in the empire of the Seljuk Turks, relying on their sometimes unreliable patronage. From Nishapur, he moved to Samarkand in Uzbekistan, and after that to Isfahan, in central Iran, where he headed the astronomical observatory for eighteen years. Political difficulties ended his support in Isfahan, and he eventually made his way to Merv in current Turkmenistan. At that time, Merv was one of the largest cities in the world. Al-Khayy
spent his working life in the empire of the Seljuk Turks, relying on their sometimes unreliable patronage. From Nishapur, he moved to Samarkand in Uzbekistan, and after that to Isfahan, in central Iran, where he headed the astronomical observatory for eighteen years. Political difficulties ended his support in Isfahan, and he eventually made his way to Merv in current Turkmenistan. At that time, Merv was one of the largest cities in the world. Al-Khayy![]() m
m![]() eventually returned to Nishapur, where he died in 1131.
eventually returned to Nishapur, where he died in 1131.
In addition to mathematics and astronomy, Al-Khayy![]() m
m![]() wrote on music and philosophy. In the West, he is best known as Omar Kayyam, the author of the famous collection of poems called the Rubaiyat.
wrote on music and philosophy. In the West, he is best known as Omar Kayyam, the author of the famous collection of poems called the Rubaiyat.
![]()
Building on the work of Greek and Islamic predecessors, al-Khayy![]() m
m![]() classified all cubic equations and solved them using geometric methods. Al-Khayy
classified all cubic equations and solved them using geometric methods. Al-Khayy![]() m
m![]() did not allow negative coefficients, so, for example, he treated x3 + x= 0 as a different type of equation from x3 = x. He also considered cubics different if they had different nonzero terms: x3 – x + 1 = 0 was in a different class than x3 + 1 = 0. (All of this was stated in words, since he did not have our notation.) In all, he identified fourteen different classes of cubics.
did not allow negative coefficients, so, for example, he treated x3 + x= 0 as a different type of equation from x3 = x. He also considered cubics different if they had different nonzero terms: x3 – x + 1 = 0 was in a different class than x3 + 1 = 0. (All of this was stated in words, since he did not have our notation.) In all, he identified fourteen different classes of cubics.
Once he had his classification, al-Khayy![]() m
m![]() proceeded to solve each class in a geometric fashion, as the intersection of two conic sections. For example, one of his classes was x3 + cx = d. He constructed a parabola, x2 =
proceeded to solve each class in a geometric fashion, as the intersection of two conic sections. For example, one of his classes was x3 + cx = d. He constructed a parabola, x2 = ![]() y, and a circle, x(d/c – x) = y2, then showed that the intersection of the parabola and circle solved the cubic, in modem terms, that the x coordinate of the intersection satisfied the equation.
y, and a circle, x(d/c – x) = y2, then showed that the intersection of the parabola and circle solved the cubic, in modem terms, that the x coordinate of the intersection satisfied the equation.
Al-Khayy![]() m
m![]() ’s approach was not unlike the way that the Greeks had solved some specific cubics many years earlier. His method was, however, more general. In a sense, he solved all cubics. But his solution was quite unlike the solution of quadratic equations by the quadratic formula. It was geometric; he did not obtain an equation for x in terms of the coefficients, to arrive at a specific number. He did make it clear that he would like such a solution, but was unable to obtain one.
’s approach was not unlike the way that the Greeks had solved some specific cubics many years earlier. His method was, however, more general. In a sense, he solved all cubics. But his solution was quite unlike the solution of quadratic equations by the quadratic formula. It was geometric; he did not obtain an equation for x in terms of the coefficients, to arrive at a specific number. He did make it clear that he would like such a solution, but was unable to obtain one.
Al-Khayy![]() m
m![]() was aware that cubics could have anywhere from zero to three solutions, and expressed this fact by the number of intersections of his conic sections. A different approach was taken by Sharaf al-Din al-Tusi, who was interested in the relationship between the number of solutions and the coefficients.
was aware that cubics could have anywhere from zero to three solutions, and expressed this fact by the number of intersections of his conic sections. A different approach was taken by Sharaf al-Din al-Tusi, who was interested in the relationship between the number of solutions and the coefficients.
Sharaf al-D![]() n
n ![]() (c. 1135-1213)
(c. 1135-1213)
Sharaf al-D![]() n
n ![]() was bom in the region of Tus in northeastern Iran. He studied astronomy and astrology as well as mathematics. He was famous as a teacher, teaching in Damascus and Aleppo in Syria, Mosul and Baghdad in Iraq.
was bom in the region of Tus in northeastern Iran. He studied astronomy and astrology as well as mathematics. He was famous as a teacher, teaching in Damascus and Aleppo in Syria, Mosul and Baghdad in Iraq.
![]()
Recall the quadratic formula
![]()
used to solve the quadratic equation, ax2 + bx + c = 0. How many solutions are there? The key is to look at the discriminant, b2 – 4ac. If this is negative, we have no solutions, since we would have to take the square root of a negative number. If b2 – 4ac = 0, then we have one solution, –b/2a. If the discriminant is positive, we have two solutions. Al-D![]() n studied cubic equations in a similar way. He made his own classification of cubics, and, in some cases, identified what we now call the discriminant of a cubic as crucial to the number of solutions. He did not, however, have any cubic equivalent of the quadratic formula.
n studied cubic equations in a similar way. He made his own classification of cubics, and, in some cases, identified what we now call the discriminant of a cubic as crucial to the number of solutions. He did not, however, have any cubic equivalent of the quadratic formula.
Sharaf al-D![]() n also gave a method for approximating the roots of a cubic equation. It was similar to that of Jia Xian, discussed in Section 2.1.
n also gave a method for approximating the roots of a cubic equation. It was similar to that of Jia Xian, discussed in Section 2.1.
Geometry
Islamic mathematicians were more interested in practical geometry than the Greeks were. They produced works on geometry intended for surveyors and artisans. Some of that work was sophisticated, for example, presenting constructions that artisans could use to produce interesting geometric figures.
There was also work on theoretical geometry, based on Greek geometry. One area of interest was Euclid’s parallel postulate. Recall (from Section 1.4) that this postulate was the wordy one which Euclid used to prove results about parallel lines.
In his Maq![]() la
la ![]() shar
shar![]() mu
mu![]()
![]() dar
dar![]() t kit
t kit![]() b Uql
b Uql![]() dis (Commentary on the Premises of Euclid’s Elements), al-Haytham attempted to remove this postulate by proving it from the others. This effort was not completely successful; he introduced a new definition of parallel lines that, unknown to him, implicitly contained the postulate. Along the way, however, he proved some important geometric theorems.
dis (Commentary on the Premises of Euclid’s Elements), al-Haytham attempted to remove this postulate by proving it from the others. This effort was not completely successful; he introduced a new definition of parallel lines that, unknown to him, implicitly contained the postulate. Along the way, however, he proved some important geometric theorems.
Ab![]() ‘Al
‘Al![]() al-
al-![]() asan ibn al-
asan ibn al-![]() asan ibn al-Haytham (Alhazen) (c. 965-1040)
asan ibn al-Haytham (Alhazen) (c. 965-1040)
Ab![]() ‘Al
‘Al![]() al-
al-![]() asan ibn al-
asan ibn al-![]() asan ibn al-Haytham, known in Europe as Alhazen, was one of the preeminent scientists of the Muslim world. He was bom in Basra, in southern Iraq, but worked much of his life in Cairo, Egypt, at the D
asan ibn al-Haytham, known in Europe as Alhazen, was one of the preeminent scientists of the Muslim world. He was bom in Basra, in southern Iraq, but worked much of his life in Cairo, Egypt, at the D![]() r al-llm (House of Knowledge), Cairo’s rival to Baghdad’s House of Wisdom.
r al-llm (House of Knowledge), Cairo’s rival to Baghdad’s House of Wisdom.
Al-Haytham’s main claim to fame is his Optics, in seven books. This was later translated into Latin, and was very influential for several centuries. Mathematically, he is best known for “Alhazen’s problem”: given a reflecting surface and two points not on the surface, find the point(s) on the surface where light emanating from the first point will, after reflection, pass through the second point. He studied this problem for several types of surfaces. It is also called Alhazen’s billiards problem: given a billiard table of a given shape (e.g., a circle), and positions of a cue ball and another ball, where should the cue ball be aimed so as to hit the other ball after one bounce?
![]()
Omar Kayyam later studied the parallel postulate, in the Sharh m![]() ashkala min mu
ashkala min mu![]()
![]() dar
dar![]() t kit
t kit![]() b Uql
b Uql![]() dis (Commentary on the Problematic Postulates of the Book of Euclid). He managed to replace it with a new postulate and show that the resulting system was equivalent to Euclid’s.
dis (Commentary on the Problematic Postulates of the Book of Euclid). He managed to replace it with a new postulate and show that the resulting system was equivalent to Euclid’s.
In 1250 Na![]()
![]() r al-D
r al-D![]() n wrote Al-ris
n wrote Al-ris![]() la al-sh
la al-sh![]() ya’an al-shakkfi-l-khu
ya’an al-shakkfi-l-khu![]()
![]() t al-mutaw
t al-mutaw![]() -ziya (Discussion Which Removes Doubt about Parallel Lines), commenting on the preceding work and attempting to prove the parallel postulate. Again, this was not successful, but it did advance understanding of the problem.
-ziya (Discussion Which Removes Doubt about Parallel Lines), commenting on the preceding work and attempting to prove the parallel postulate. Again, this was not successful, but it did advance understanding of the problem.
Na![]()
![]() r al-D
r al-D![]() n
n ![]() (1201-1274)
(1201-1274)
Na![]()
![]() r al-D
r al-D![]() n
n ![]() , not to be confused with Sharaf al-D
, not to be confused with Sharaf al-D![]() n
n ![]() , was also from Tus in Iran. He studied there and at Nishapur. This was a time of political upheaval, culminating in the Mongol conquest of the area, so Na
, was also from Tus in Iran. He studied there and at Nishapur. This was a time of political upheaval, culminating in the Mongol conquest of the area, so Na![]()
![]() r al-D
r al-D![]() n traveled extensively. He eventually settled in Maragha in northwestern Iran, were he founded an important astronomical observatory.
n traveled extensively. He eventually settled in Maragha in northwestern Iran, were he founded an important astronomical observatory.
Na![]()
![]() r al-D
r al-D![]() n was prolific, reportedly authoring more than 150 texts on many scientific and religious subjects. He was one of the most influential astronomers in the time between Ptolemy and Copernicus.
n was prolific, reportedly authoring more than 150 texts on many scientific and religious subjects. He was one of the most influential astronomers in the time between Ptolemy and Copernicus.
![]()
Another area of Euclid that Islamic mathematicians studied was incommensu- rables. In Book X of the Elements, Euclid dealt with incommensurable magnitudes, those which have no common measure. In modem terms, their ratio is an irrational number. Magnitudes were not the same as numbers, however. One could not compare areas and lengths, for example.
In practice, Islamic mathematicians dealt with numbers, not magnitudes, but they were aware of the logical difficulties this caused, particularly when dealing with irrationals. Some attempts were made to justify the Islamic approach in ways of which Euclid would have approved. One such was in Ris![]() la fi’-maq
la fi’-maq![]() dir al-mushtaraka wa ’l-mutab
dir al-mushtaraka wa ’l-mutab![]() yana (Treatise on Commensurable and Incommensurable Magnitudes), published around 1000 by Ab
yana (Treatise on Commensurable and Incommensurable Magnitudes), published around 1000 by Ab![]() ‘Abdall
‘Abdall![]() h al-
h al-![]() asan ibn al-Baghd
asan ibn al-Baghd![]() d
d![]() .
.
In this work, ibn al-Baghd![]() d
d![]() developed a logical foundation in which he could treat all magnitudes as lengths of lines. His system worked for rational numbers and square roots, as well as square roots of square roots, and so on. Along the way, he proved an intriguing result about the density of irrationals, namely, that between any pair of rational numbers there exist an infinite number of irrational numbers.
developed a logical foundation in which he could treat all magnitudes as lengths of lines. His system worked for rational numbers and square roots, as well as square roots of square roots, and so on. Along the way, he proved an intriguing result about the density of irrationals, namely, that between any pair of rational numbers there exist an infinite number of irrational numbers.
Mathematical Induction
As mentioned in Section 2.2, ![]() ryabhata gave the following formula for the sum of cubes:
ryabhata gave the following formula for the sum of cubes:
![]()
He did not, however, write down a proof. The first to do this was al-Karaj![]() , at least for n = 10. It is clear that his argument would work for any n. Here it is.
, at least for n = 10. It is clear that his argument would work for any n. Here it is.
Figure 2.15 Proving that l3 + 23 + … + 103 = (1 + 2 + … + 10)2.
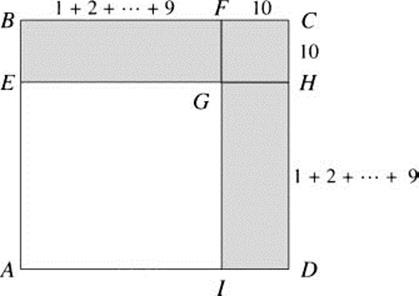
Consider the square ABCD in Figure 2.15. We will compute its area S in two ways. First, since one side has length 1 + 2 + … + 10, we have
![]()
Now consider the shaded area. It is composed of three pieces. The area of the rectangle BFGE is 10(1 + 2 + … + 9), as is the area of GHDL Finally, the little square FCHG has area 102. Putting this together, we have the shaded area equaling
![]()
Since S is just the shaded area plus the unshaded area, which is a square of side 1 + 2 + … + 9, we can write
![]()
Next, we use the formula 1 + 2 + 3 + … + n = n(n + 1)/2 to write
![]()
Therefore
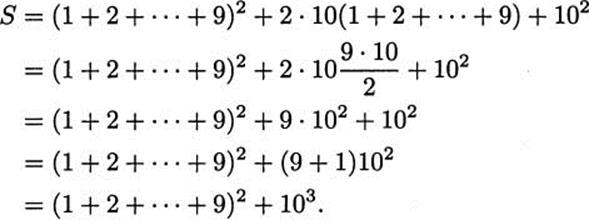
Combining this with our first equation for S yields
![]()
Note that we have now reduced the problem to studying (1 + 2 + … + 9)2. But the same argument shows that
![]()
So
![]()
Repeating, we get
![]()
Continuing in this way, we finally arrive at
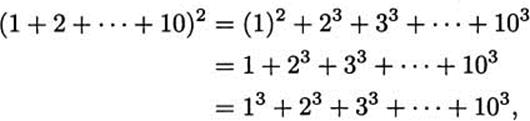
which is what we sought to prove.
A notable feature of this argument is how al-Karaj![]() reduced the case with n = 10 to the one with n = 9, then n = 8, etc., until the case n = 1, which is trivial. This is the essence of the type of argument we now call mathematical induction, one of the most powerful tools of modem mathematics.
reduced the case with n = 10 to the one with n = 9, then n = 8, etc., until the case n = 1, which is trivial. This is the essence of the type of argument we now call mathematical induction, one of the most powerful tools of modem mathematics.
A similar type of argument was used by al-Haytham to prove a formula for sums of fourth powers, which he needed in his study of Alhazen’s problem. Let us recall a couple of formulas we have seen before.
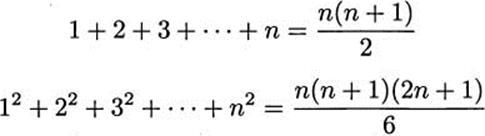
These formulas were known well before al-Haytham’s time, in word form, without our notation. Known as well was the formula for the sum of cubes:
![]()
Al-Haytham extended this to the sum of fourth powers:
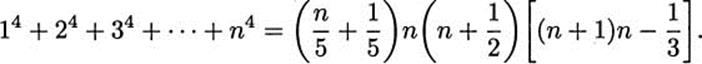
His argument could easily be extended, with a lot of computation, to find a formula for the sum of fifth powers, then sixth, and so on, but he stopped at fourth powers.
Although al-Karaj![]() , al-Haytham, and others used arguments that were much like mathematical induction, an explicit statement of mathematical induction, and its widespread use, was centuries away.
, al-Haytham, and others used arguments that were much like mathematical induction, an explicit statement of mathematical induction, and its widespread use, was centuries away.
Trigonometry
Islamic scholars learned of trigonometry from the Greeks and the Indians. As with these earlier cultures, the important motivation came from astronomy. Muslims had extra reasons to study astronomy. They were (and are) required to pray five times a day, facing Mecca. The astronomers needed to determine the direction of Mecca, and the time of day. Some of the early “Islamic” astronomers were also associated with the Sabean religion, which was centered around celestial objects. In addition, as always, there was astrology.
There are six standard trigonometric functions in modem mathematics. We introduced the sine, cosine, and tangent in Section 1.5. The other three are the cotangent, secant, and cosecant.
![]()
The full list of these six functions first appeared in the 9th century. Before then, only the sine and cosine were in use, although the tangent had made a brief appearance in China in the previous century. (Actually, the Muslims’ trigonometric functions were constant multiples of ours, a minor difference.)
An important early text was an astronomy book, the Z![]() j al-Majisti, by Ab
j al-Majisti, by Ab![]() al- Waf
al- Waf![]() . This work contained, in addition to the six trigonometric functions, some fundamental results in spherical trigonometry. Recall that spherical trigonometry is concerned with triangles on a sphere. This was important in astronomy both because the Earth is (nearly) a sphere, and because the sky can be treated as a sphere. In fact, the simpler plane trigonometry, as taught in high school courses now, mostly developed after the more complicated spherical trigonometry, because astronomy was the central application.
. This work contained, in addition to the six trigonometric functions, some fundamental results in spherical trigonometry. Recall that spherical trigonometry is concerned with triangles on a sphere. This was important in astronomy both because the Earth is (nearly) a sphere, and because the sky can be treated as a sphere. In fact, the simpler plane trigonometry, as taught in high school courses now, mostly developed after the more complicated spherical trigonometry, because astronomy was the central application.
Ab![]() al-Waf
al-Waf![]() al-B
al-B![]() zj
zj![]() ni (940–998)
ni (940–998)
Ab![]() al-Waf
al-Waf![]() al-B
al-B![]() zj
zj![]() ni was bom in Khorasan, in the northeastern part of modernday Iran. He worked in Baghdad, under the Buyid dynasty, which for a time was a great supporter of science. Ab
ni was bom in Khorasan, in the northeastern part of modernday Iran. He worked in Baghdad, under the Buyid dynasty, which for a time was a great supporter of science. Ab![]() al-Waf
al-Waf![]() helped design and build a major observatory there in 988.
helped design and build a major observatory there in 988.
In addition to his theoretical work, Ab![]() al-Waf
al-Waf![]() wrote a business text called Book on What Is Necessary from the Science of Arithmetic for Scribes and Businessmen. Even though he was conversant with Hindu numerals, Ab
wrote a business text called Book on What Is Necessary from the Science of Arithmetic for Scribes and Businessmen. Even though he was conversant with Hindu numerals, Ab![]() al-Waf
al-Waf![]() wrote numbers in this book in words, and computations were done using fingering-reckoning. This was what businessmen of his day used. Also notable is his use of negative numbers, very rare in Islamic mathematics. They were useful in business to represent debts.
wrote numbers in this book in words, and computations were done using fingering-reckoning. This was what businessmen of his day used. Also notable is his use of negative numbers, very rare in Islamic mathematics. They were useful in business to represent debts.
![]()
A younger contemporary of Ab![]() al-Waf
al-Waf![]() , Ab
, Ab![]() 1-R
1-R![]() y
y![]() an Mu
an Mu![]() ammad ibn A
ammad ibn A![]() mad al-B
mad al-B![]() r
r![]() n
n![]() , also mastered the various trigonometric functions, and established a number of relations between them. He applied his knowledge to astronomy, among other things, giving a method to calculate the direction to Mecca from any location, and inventing a new method to estimate the radius of the Earth, obtaining a result about 20% too small.
, also mastered the various trigonometric functions, and established a number of relations between them. He applied his knowledge to astronomy, among other things, giving a method to calculate the direction to Mecca from any location, and inventing a new method to estimate the radius of the Earth, obtaining a result about 20% too small.
Ab![]() 1-R
1-R![]() y
y![]() an Mu
an Mu![]() ammad ibn A
ammad ibn A![]() mad al-B
mad al-B![]() r
r![]() n
n![]() (973-1055)
(973-1055)
Ab![]() 1-R
1-R![]() y
y![]() an Mu
an Mu![]() ammad ibn A
ammad ibn A![]() mad al-B
mad al-B![]() r
r![]() n
n![]() was bom in Khwarizm, near Biruni in modern-day Uzbekistan. He lived in a time of political turmoil, and had to spend considerable time courting royal sponsors or fleeing from them. He was employed as an astrologer, although he privately rejected it, and was an accomplished diplomat. He wrote, “I was compelled to participate in worldly affairs, which excited the envy of fools, but made the wise pity me.”
was bom in Khwarizm, near Biruni in modern-day Uzbekistan. He lived in a time of political turmoil, and had to spend considerable time courting royal sponsors or fleeing from them. He was employed as an astrologer, although he privately rejected it, and was an accomplished diplomat. He wrote, “I was compelled to participate in worldly affairs, which excited the envy of fools, but made the wise pity me.”
Al-B![]() r
r![]() n
n![]() wrote over 140 works, most importantly on astronomy, mathematics, and geography. His book India, in which he addressed all aspects of Indian culture, is still important. In astronomy, he notably proposed that the Earth travels around the Sun.
wrote over 140 works, most importantly on astronomy, mathematics, and geography. His book India, in which he addressed all aspects of Indian culture, is still important. In astronomy, he notably proposed that the Earth travels around the Sun.
![]()
Islamic mathematicians also made tables of trigonometric functions. Ab![]() al-Waf
al-Waf![]() invented a new method to approximate sine values, which allowed him to create a sine table accurate to four sexagesimal places. (Astronomers were still using the Babylonian sexagesimal system.)
invented a new method to approximate sine values, which allowed him to create a sine table accurate to four sexagesimal places. (Astronomers were still using the Babylonian sexagesimal system.)
Eventually, trigonometry came to be considered a mathematical subject in its own right, not solely as part of astronomy. This culminated in the Kit![]() b al-Shakl al-qatt
b al-Shakl al-qatt![]() (!Treatise on the Complete Quadrilateral), by Na
(!Treatise on the Complete Quadrilateral), by Na![]()
![]() r al-D
r al-D![]() n
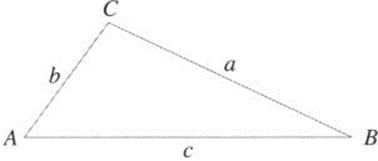
n ![]() , a comprehensive work on plane and spherical trigonometry. It has the first statement and proof of the law of sines for plane triangles. Referring to Figure 2.16, the law of sines is the following.
, a comprehensive work on plane and spherical trigonometry. It has the first statement and proof of the law of sines for plane triangles. Referring to Figure 2.16, the law of sines is the following.
![]()
Figure 2.16 Notation for the law of sines.
The word sine came to us by a roundabout path. In Sanskrit, jy![]() -ardha means “chord-half.”
-ardha means “chord-half.” ![]() ryabhata abbreviated this to jy
ryabhata abbreviated this to jy![]() , or its synonym j
, or its synonym j![]() v
v![]() . When his works were translated into Arabic, j
. When his works were translated into Arabic, j![]() v
v![]() became jiba, which does not mean anything, but sounds about the same. In Arabic, however, vowels are not written, so this word was written jb. Later Arabic writers confused this with the word jaib, which means “breast.” When Arabic trigonometry was translated into Latin, the Latin word for “breast,” sinus, was used, leading to our sine.
became jiba, which does not mean anything, but sounds about the same. In Arabic, however, vowels are not written, so this word was written jb. Later Arabic writers confused this with the word jaib, which means “breast.” When Arabic trigonometry was translated into Latin, the Latin word for “breast,” sinus, was used, leading to our sine.
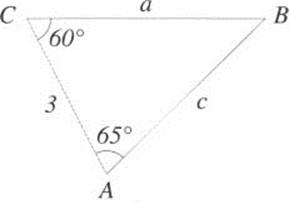
The law of sines is a useful tool for solving a common type of problem in geometric applications. This problem occurs when we have measurements of some sides and angles in a triangle, and wish to determine the unknown sides and angles. This is called solving the triangle. In addition to the law of sines, other tools for solving triangles include the Pythagorean Theorem, and the fact the sum of angles in a triangle is 180°.
As an example, we will solve the triangle in Figure 2.17, i.e., find sides b and c, and angle B. We first note that, since the sum of angles is 180°, angle B must be 25°. Then we use the law of sines to write
![]()
Solving these equations, we get
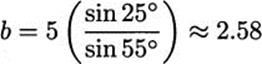
and
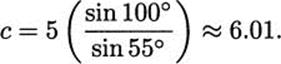
Figure 2.17 Solving a triangle.
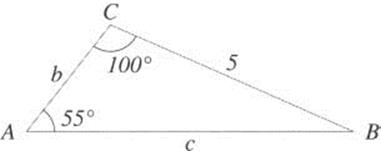
Finally, we mention the work of al-K![]() sh
sh![]() in the 15th century. He came up with a better approximation method, one that enabled Ul
in the 15th century. He came up with a better approximation method, one that enabled Ul![]() gh Beg to approximate the sine of one degree, accurate to 16 decimal places. Ul
gh Beg to approximate the sine of one degree, accurate to 16 decimal places. Ul![]() gh Beg, al-K
gh Beg, al-K![]() sh
sh![]() ’s patron and ruler of a sizable central Asian kingdom, was also an astronomer. He used al-K
’s patron and ruler of a sizable central Asian kingdom, was also an astronomer. He used al-K![]() sh
sh![]() ’s method to produce tables for sines and tangent for every minute of arc (one-sixtieth of a degree), to five sexagesimal places. This must have been an enormous effort, producing 10,800 (= 60 o 90 o 2) entries. Perhaps he was more interested in this work than in governing. He wasn’t very successful at the latter; his son eventually had him killed.
’s method to produce tables for sines and tangent for every minute of arc (one-sixtieth of a degree), to five sexagesimal places. This must have been an enormous effort, producing 10,800 (= 60 o 90 o 2) entries. Perhaps he was more interested in this work than in governing. He wasn’t very successful at the latter; his son eventually had him killed.
Ghiy![]() th al-D
th al-D![]() n Jamsh
n Jamsh![]() d al-K
d al-K![]() sh
sh![]() (c. 1380–1429)
(c. 1380–1429)
Ghiy![]() th al-D
th al-D![]() n Jamsh
n Jamsh![]() d al-K
d al-K![]() sh
sh![]() was bom in Kashan in central Iran. He was one of the greatest of the Islamic astronomers and mathematicians. His early years were quite difficult; this was the time when Timur (also known as Tamerlane or Tamburlaine) was conquering much of western Asia.
was bom in Kashan in central Iran. He was one of the greatest of the Islamic astronomers and mathematicians. His early years were quite difficult; this was the time when Timur (also known as Tamerlane or Tamburlaine) was conquering much of western Asia.
Timur’s grandson, Ul![]() gh Beg, built a major center of learning in his capital city of Samarkand, and invited al-K
gh Beg, built a major center of learning in his capital city of Samarkand, and invited al-K![]() sh
sh![]() to join him there. al-K
to join him there. al-K![]() sh
sh![]() did his most important work in Samarkand.
did his most important work in Samarkand.
![]()
In the years 800–1400, Islamic mathematicians were the best in the world. During much of this time, however, as at many other times and in many other places, support for higher mathematics was uncertain. Scholars depended on the patronage of the rulers, and many rulers did not consider mathematics important, beyond the obvious practical applications. By the 11th century, there was diminished support for theoretical mathematics. Some in Islam considered it a “foreign” science. It always was thought of as inferior to religious studies. Nonetheless, advances continued, if at a slower pace. It was not until the 16th century that European mathematicians clearly outshone their Islamic counterparts.
EXERCISES
2.32 Solve.
a)2x + 7 = 8 – x
b)2x2 + 2 = 5x
c)x + x3 = 3x
2.33 Al-Khw![]() rizm
rizm![]() solved x2 + 10x = 39 to get x = 3.
solved x2 + 10x = 39 to get x = 3.
a) There is another solution. Find it.
b) Why do you think al-Khw![]() rizm
rizm![]() did not give this solution?
did not give this solution?
2.34 Complete Abu K![]() mil’s solution of
mil’s solution of
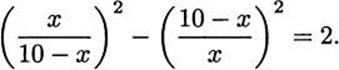
2.35 Evaluate 2x2 + 3x + 4 + 5x –1 + 6 –2 at x = 10.
2.36 We saw how Al-Khw![]() rizm
rizm![]() solved x2 + lOx = 39. Use a diagram like Fig 2.14 to find a positive solution to x2 + 6x = 91. Include an argument like Al-Khw
solved x2 + lOx = 39. Use a diagram like Fig 2.14 to find a positive solution to x2 + 6x = 91. Include an argument like Al-Khw![]() rizm
rizm![]() ’s to show how your diagram leads to your solution.
’s to show how your diagram leads to your solution.
2.37 Classify cubics like al-Kayy![]() m
m![]() did. Do you get fourteen classes?
did. Do you get fourteen classes?
2.38 Find out, by looking at the discriminant, how many solutions each of the following equations has.
a)x2 – 3x + 7 = 0
b)2x2 – 5x + 2 = 0
c)3x2 – 11 = 0
d)4x2 – 17x + 5 = 0
2.39 Consider the cubic equation x3 + 4x = 12. In the text, we mention that al-Kayy![]() m
m![]() solved this cubic as the intersection of a parabola and a circle.
solved this cubic as the intersection of a parabola and a circle.
a) What are the equations of the parabola and the circle in this case?
b) Show that the intersection does actually solve the cubic. (Hint: use the equation of the parabola to solve for y in terms of x, then plug this value for y into the equation of the circle, and simplify.)
2.40 Use the formula l3 + 23 + … + n3 = (1 + 2 + … + n)2 to calculate 13 + 23 + … + 103. (Hint: recall that 1 + 2 + … +n = n(n + l)/2.)
2.41 Use al-Haytham’s formula to calculate l4 + 24 + … + 104.
2.42 Solve the triangle.
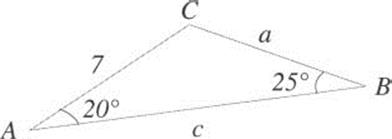
2.43 Solve the triangle.