Numbers: Their Tales, Types, and Treasures.

Chapter 1: Numbers and Counting

1.14.MEASURING MAGNITUDES

Natural numbers are “counting numbers.” They can be used to count every finite collection of arbitrary things; they measure the size of a set. But there is an even more important aspect of numbers that we have not covered yet, and that goes beyond just natural numbers. In everyday life, we use numbers not so much to measure sets but to measure and describe quantities and magnitudes. These entities cannot be counted in a strict sense. For example, the length of a line segment is a magnitude—in itself it is something quite different from a natural number, which, as we have just seen, describes the cardinality of a set. How is it that we can express lengths through numbers?

The key idea here is to measure a length in multiples of unit lengths. The choice of units is a mere matter of convention. In practice, the unit is provided by the measuring device that we use to measure the given quantity. For measuring lengths we have, for example, a measuring tape or a ruler with the units printed on it. By comparing a given length with the ruler and its units, we determine a measuring number that describes the length. For example, in figure 1.10, we find that seven unit lengths in a row add up to give us the length of a stick. We see that measuring lengths is just another form of counting.

Figure 1.10: Measuring lengths is done by counting units.

What do we do when the length of the object does not fit exactly to a whole number of units, as in figure 1.11? In this case, we first count the number of whole units that measure the length of the stick. This gives two inches. Now there is a remainder that is shorter than one inch. The given length is not a multiple of the unit. In that case, we divide the unit into suitable subunits and count the remainder in these subunits. A subunit is always a fraction of the given unit, which means the subunit is given as one n^th of the unit. For example, one could take inch as a subunit for one inch, as in figure 1.11, where we count seven of these subunits. This means that the length of the stick is two inches plus seven times of an inch, which is usually written as 2 ".

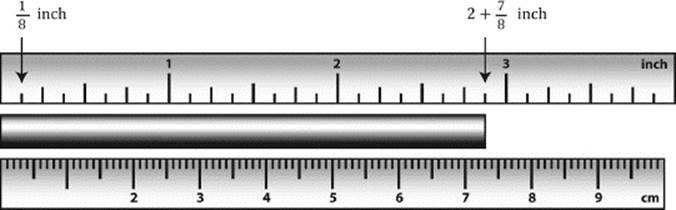
Figure 1.11: Measuring lengths with units and subunits.

Metric units are usually divided into ten parts. One tenth of a centimeter is a millimeter. The same stick would then have a length of 7 cm and 3 mm. For the division of units into ten parts, we have a convenient notation that is an extension of the place-value system described in theprevious section: We write 7.3 (seven point three) when the magnitude is given by seven units and three tenths of that unit. And if we need a higher accuracy, we could divide smaller subunits even further. With more precise methods, we would find that a stick of 2 and inches would measure 7.3025 cm, which means 7 units + 3 tenths + 2 thousandths + 5 ten-thousandths.

Notice that we have the role of the zero symbol as a place holder, denoting the absence of hundredths in this case.

We call a number that measures a quantity by comparison with a given unit a real number. An important special case is a rational number. A rational number describes a quantity as a multiple of a unit plus a multiple of a subunit, as, for example, in 2 plus inches or 7 plus centimeters or 5 plus gallons. In all these cases, it is possible to express the quantity as an integer multiple of a suitably chosen subunit:

It has come as a surprise that this cannot be done in all cases. Not every length can be described as an integer multiple of a unit plus an integer multiple of a subunit. Such a number would be called irrational—as distinguished from the rational numbers shown in the examples above. In other words, an irrational number cannot be expressed as a fraction. An example of an irrational number is the length of the diagonal of a unit square—one whose side length is one. The length d of the diagonal of the unit square is the square root of two or, written symbolically, d = = 1.41421356….

This means that the length of the diagonal equals the length of the side plus four tenths of the side, plus one hundredth of the side, plus four thousandths, plus two ten-thousandths, and so on. The chain of digits behind the dot will never end. This alone would not make d irrational, as the example with 5.33333…= 5 shows. This number has also infinitely many digits in the base-10 representation, but these digits are all the same. In contrast, there is no repetitive pattern in the digits of d = . And one can show that it is not possible to write d as a multiple of a certain fraction of the unit, which makes it irrational.

Another famous example of an irrational number is

π = 3.14159…

The measure of the circumference of a circle, using the diameter of that circle as the unit of length equals three times the diameter of the circle, plus one tenth of the diameter, plus four hundredths of the diameter, plus…. Again, the chain of digits would never end and follows no regular pattern (no periodic repetitions). Thus the number π is irrational: it cannot be written as a multiple of a fraction of the unit. More about this amazing number π will be discussed in chapter 10.

Provided that a unit (a “gauge”) is fixed, magnitudes of all kinds can be measured by the same type of real number, and in quite a similar way as we measure lengths. We measure areas by square meters and volumes by cubic meters or similar units. We measure time by counting hours, minutes, and seconds. It is quite interesting that hours and minutes have sixty subunits, which reminds us of the ancient Babylonian numeral system (see chapter 3).

Thus, we now have a better understanding of the nature and development of how numbers were represented over time to where we now have a rather sophisticated system for representing quantities.