Numbers: Their Tales, Types, and Treasures.

Chapter 2: Numbers and Psychology

2.9.IDIOSYNCRASIES OF LANGUAGES

A useful sequence of number words has to follow some principles: For example, all words have to be unique. There should be no words used for numbers that sound the same, and refer to various numbers. Moreover, the counting sequence should be nonterminating. This can be achieved on the basis of a systematic, hierarchical method of grouping, as explained in chapter 1. The system of counting with the help of sticks, shells, pebbles, and the like, would then be reflected in the construction of number words. A general system of forming number words with base number 10 is shown in table 2.1. This system was invented in various parts of the world and is still in use in China. Although the English counting system is somewhat different, it is very similar to the system of table 2.1 in the case of higher numbers. For example, “nine-hundred-nine-ten-three” in table 2.1 is obviously the same as the English numeral “nine-hundred-ninety-three.”

Table 2.1 shows a general scheme of creating number words using addition (“ten-two” means “ten plus two”) as well as multiplication (“two-ten” means “two times ten”). Because the grouping is based on the number 10, this counting system needs number words for the basic digits from 1 to 9, and words for the higher units, such as ten, hundred, thousand, and so on. Higher numerals are typically formed by combining words from a higher rank (like “two thousand”) with words from a lower rank (like “three hundred” and “sixty-seven”) to form a new word (“two thousand three hundred sixty-seven”).

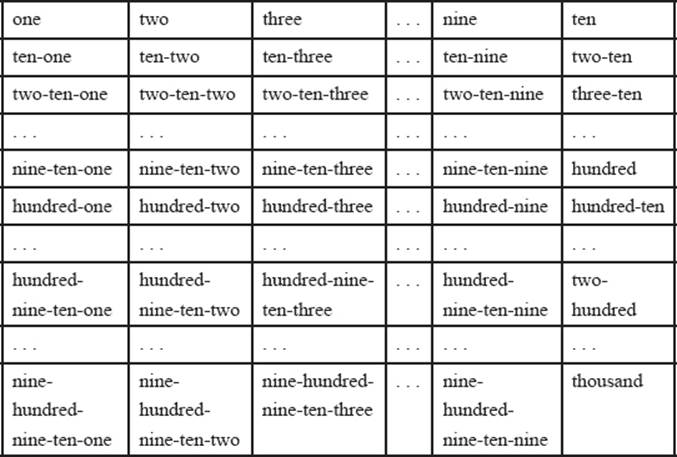
Table 2.1: A systematic number-word sequence.

Life would be easier for children learning arithmetic if the number words would always follow this strict building rule, as it is indeed the case in China, Japan, and Korea. The Chinese number system is built with an exceptional regularity and follows (almost) exactly the system of table 2.1. They have special words for the numbers 1,…, 10, and then for 100, 1,000, and 10,000, and they construct other numbers recursively: After counting to ten, they start again by adding the number words one to nine as a suffix to the base ten, until one reaches “two-ten,” and so on, exactly as shown in table 2.1.

This scheme of table 2.1 combines multiplication and addition. Compare two-ten (meaning two times ten) and ten-two (meaning ten plus two). The multiplier is always a word of lower rank, set before a word of higher rank. A word with lower rank set behind the higher-rank word is meant additively. This is also the building principle for higher numbers, where some powers of 10 have no special name. While there is a special numeral for ten thousand in Chinese, there is no such word in English, and the numeral is constructed by the multiplicative principle (ten thousand = ten times one thousand). Similarly, two hundred thousand means two times hundred times thousand, but two thousand hundred means two times thousand plus hundred.

The English system of number words essentially follows this scheme, as far as larger numbers are concerned—as is the case with many other languages. But there are many exceptions for smaller numbers. In English, it is twenty and not “two-ten,” and it is thirteen instead of “ten-three.” It should be noted that in American English the usage of the word and anywhere in a numeral is discouraged (“five hundred seventy-eight,” except when indicating a decimal point's placement, as in “fifty-six and three tenths”), whereas in British English it is common to say “five hundred and seventy-eight.” Moreover, there are some irregularities in vernacular use, like “two-oh-seven” in American English instead of “two hundred seven” or “twenty-two fifty-one” instead of “two thousand two hundred fifty-one.”

It can be assumed that more idiosyncrasies and exceptions lead to more difficulties for children to grasp the overall organization of the counting sequence, and to more difficulties in understanding the relationship of number words to their written form. And it makes arithmetic more difficult (“ten plus two is ten-two” would be easier to learn than “ten plus two is twelve”). Comparative studies have indeed shown that first graders in China, Japan, and Korea have a better understanding of the base-10 structure of the numeral system and of the place-value system in number notation than their American counterparts.

Similar deviations from the logical structure of the counting system occur in many languages, but, as in English, the exceptions are always restricted to the small numbers. Lower numbers appeared first in history, and they are often used on a daily basis. Therefore, they are often easily changed by idiomatic usage and manners of speaking.

For example, in Latin, subtraction appears in some places. The Latin word for nineteen is un-de-viginti (one-off-twenty) and the word for eighteen is duo-de-viginti (two-off-twenty). In Finnish, the words for numbers 11 to 19 are constructed by adding toista, meaning second. So the numeral for sixteen describes that this number has the sixth place in the second block of numbers (kuusi-toista = “six second”). In French, the numbers between 60 (soixante) and 100 (cent) reflect an old use of a vingesimal system (a numeral system with base-20). So they have no word for seventy, using soixante-dix (sixty-ten) instead. The word for eighty is quatre-vingt (meaning four-twenty), and ninety would be quatre-vingt dix (meaning four-twenty-ten). Italian has special words for 11 to 16 (un-dici,…se-dici) and then changes the building principle for 17 to 19 (dici-assette, dici-otto, dici-annove).

In German, there is a separate building principle for all words up to 100. The word for 23 would be dreiundzwanzig, meaning “three and twenty,” which reverses the written order of digits. It also violates the general rule that words of lower rank set before a word of higher rank would imply a multiplication. Therefore, the addition is spelled out explicitly (the und in between drei and zwanzig).

As we have seen in chapter 1, a base-10 system, although predominant in our time, is not the only possible numeral system. Moreover, from the spoken numerals, it is still a long way from being a useful system of notation. In the next chapter, we will look into the history of various systems of writing numbers.