Numbers: Their Tales, Types, and Treasures.
Chapter 4: Discovering Properties of Numbers
4.6.TRIANGULAR AND RECTANGULAR
By looking at figure 4.11, we see another interesting relationship for triangular numbers: Adding two consecutive triangular numbers obviously gives a square number. With just a little manipulation, we can see that happening geometrically.
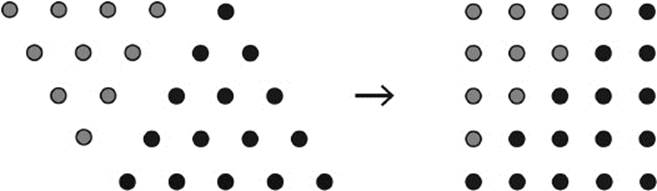
Figure 4.11: Triangular numbers and square numbers.
The relationship expressed in figure 4.11 means that every square number is the sum of two consecutive triangular numbers. In formulas, this statement can be elegantly and simply written as
Tn–1 + Tn = n2 (for all natural numbers n greater than 1).
A similar observation can be made with the help of figure 4.12. Taking the same triangular number twice obviously produces a rectangular number, where the number of columns exceeds the number of rows by one.
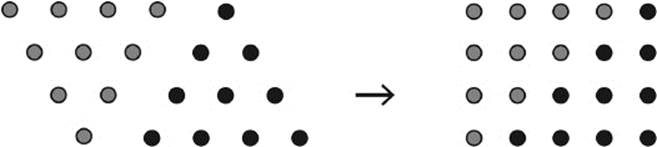
Figure 4.12: Twice a triangular number gives a rectangular number n × (n + 1).
This can be written as 2 × Tn = n × (n + 1). From this we obtain a useful formula,
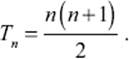
With this formula, we can compute the nth triangular number immediately, without having to compute the sum of all natural numbers up to n. Note that either n or n + 1 must be an even number and can be easily divided by two. Thus, the formula really just requires us to evaluate a single multiplication. And this multiplication is equivalent to summing up all integers from 1 to n. Hence, for example, the sum of the first 100 natural numbers is easily obtained as
![]()
This particular triangular number often occurs in an anecdote about Carl Friedrich Gauss (1777–1855), one of the most important mathematicians of all time. Wolfgang Sartorius von Waltershausen, an early biographer, tells several stories of Gauss being a child prodigy with almost unbelievable skills in mental arithmetic. One of these stories (which Gauss himself often related in old age with amusement) is about nine-year-old Carl Friedrich at his elementary school, where a stern teacher confronted his students with the task of summing an arithmetic series. Much to the surprise of his teacher, Gauss produced the correct solution immediately, while all his classmates continued calculating for a very long time—producing wrong results in most cases. Later biographers beefed the story up with more mathematical details, claiming that the arithmetic series was the first 100 integers, and they also provided a method for how Gauss could have obtained the result 5050. Usually, this trick is explained as follows: In order to sum all integers between 1 and 100, young Carl Friedrich started by adding numbers from opposite ends of the sequence, that is, 1 + 100, then 2 + 99, 3 + 98, and so on. He observed that in each case the sum is 101. The last sum in this sequence would be 50 + 51, which shows that there is a total of fifty such sums, of 101. Hence the answer is 50 × 101 = 5050, as shown in figure 4.13.

Figure 4.13: Gauss's trick for adding up all numbers from 1 to 100.
If you indeed try to solve the problem in the straightforward way—that is, by actually adding up all the numbers between 1 and 100—you will soon notice that this tends to be a rather tedious task. Obviously, a sudden flash of genius can really be helpful to solve a mathematical problem like this. But usually we cannot count on having this type of inspiration just when we need it. Much of mathematical research, thus, aims at developing methods that spare us the necessity of having ingenious ideas whenever we have to solve a mathematical problem. Our knowledge of triangular numbers obtained in this section would help us to add all natural numbers up to some value of n with similar speed as that of young Carl Friedrich Gauss. The formula for Tn effectively reduces this to a routine task—a simple multiplication.