Numbers: Their Tales, Types, and Treasures.
Chapter 4: Discovering Properties of Numbers
4.8.TETRAHEDRAL NUMBERS
For the sake of completeness, we mention that the polygonal numbers have generalizations to higher dimensions. Points can be arranged in space to form regular polyhedrons. An example would be the stacking of cannon balls, as in figure 4.17, which realizes one of the Platonic solids, the tetrahedron.
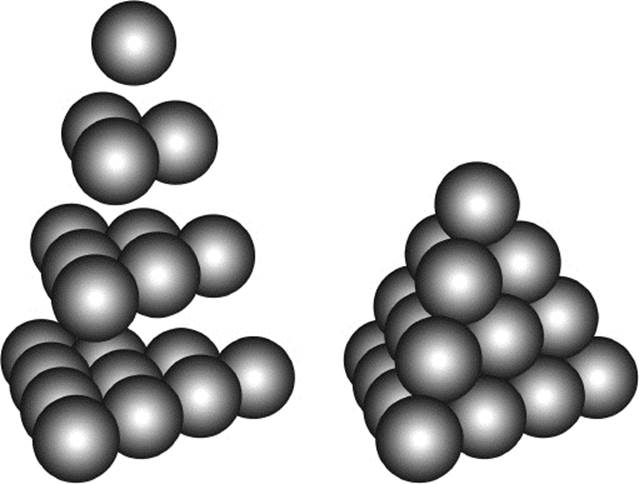
Figure 4.17: Tetrahedral stacking of cannon balls.
The left view shows the individual layers of the arrangement. We see that all layers are consecutive triangular numbers. Hence the number of cannonballs in the tetrahedral stack, where the side line of the base has four balls, is just the sum of the first four triangular numbers, 1 + 3 + 6 + 10 = 20. The sequence of tetrahedral numbers obtained in this way starts with
1, 4, 10, 20, 35, 56, 84, 120, 165, 220…
We will encounter these numbers again in a completely different context in the next chapter.