Numbers: Their Tales, Types, and Treasures.

Chapter 6: Number Explorations

6.4.COMBINATORIAL GEOMETRY

What makes the Pascal triangle so truly outstanding is the many fields of mathematics it touches or involves. We have seen in chapter 5, section 11, how the Pascal triangle arises in the theory of lotto games (probability theory). For sheer enjoyment, we shall consider some more applications of the Pascal triangle now.

In table 6.3 we have listed circles in the first column with an increasing number of points on the circle. With the circles that have two or more points, we have drawn all possible connecting segments. Each column lists the number of polygons that one can count in the figure shown in the first column of that row. You will notice that we have essentially created the Pascal triangle with the exception of the first 1 at the left (except for the top 1). The reason for the appearance of the Pascal triangle in table 6.3 can be understood as follows: In chapter 5, we denoted the number in the Pascal triangle that is n steps down from the top and k steps from the left border by B(n,k) (e.g., B(7,2) = 21). According to chapter 5, section 11, the number B(n,k) equals the number of all k-element subsets of an n-element set. Consider, for example, the number of line segments connecting two of the vertices of a heptagon. Obviously, this is the same as the number of 2-vertex subsets of the set of seven vertices, that is, B(7,2) = 21 (which is indeed the number in line 7 and column 2 of table 6.3). Similarly, each triangle formed from the vertices of a heptagon corresponds to a choice of three vertices out of the given seven vertices. Hence the number of those triangles is equal to the number of 3-vertex subsets, that is, B(7,3) = 35.

The Pascal triangle can also help us predict into how many pieces a plane can be divided by a given number lines, where no two are parallel and no three are concurrent (i.e., containing a common point of intersection). Figure 6.7 shows that three lines can divide the plane into seven regions, and four lines can divide the plane into eleven regions. The condition is that no two lines are parallel, and not more than two lines intersect at the same point.

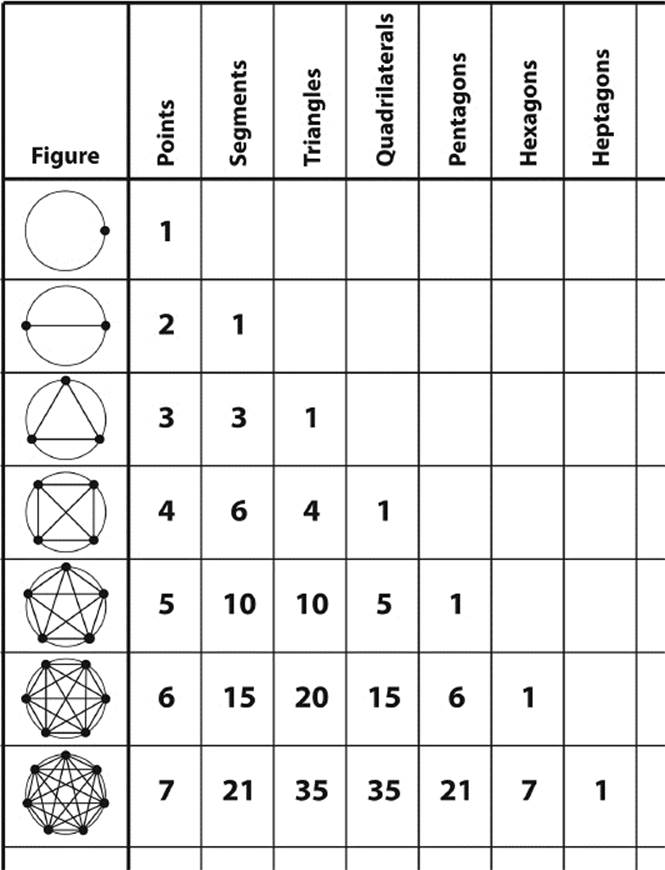
Table 6.3: Numbers of cyclic polygons.

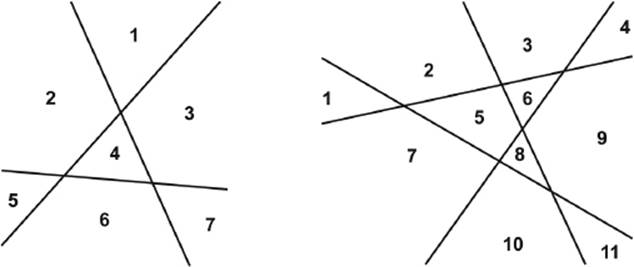
Figure 6.7: Regions formed by three or four lines in a plane.

Among other information, these numbers are listed in the chart in table 6.4. Just wait a bit and you will see how this ties in with the Pascal triangle.

Table 6.4: Number of geometric partitions.

For example, when there are three points on the line, the line is partitioned into four line segments. Or, consider the case with five lines in a plane intersecting in such a way that no two lines are parallel and no three lines are concurrent, we find that there are sixteen regions determined. This should give you some idea as to how the numbers in the chart have been generated. But now we shall see how the Pascal triangle could also have generated these numbers.

The columns of the chart can be obtained from the Pascal triangle by taking the sum of the shaded elements in each of the rows, as shown in figure 6.8.

Figure 6.8: Partial sums of the rows in the Pascal triangle.