Numbers: Their Tales, Types, and Treasures.

Chapter 7: Placement of Numbers

7.2.GENERAL PROPERTIES OF MAGIC SQUARES

You might wonder how it could be that both the Chautisa Yantra and the Dürer magic square have 34 as their “magic number.” But, actually, this would necessarily be the case for any 4 × 4 magic square that uses the numbers from 1 to 16. The sum of these numbers is 1 + 2 + 3 +…+ 16 = 136. In a magic square, every row of numbers contributes exactly a quarter of this sum because there are four rows and all rows are required to have the same sum. Therefore, the sum across each row is a quarter of 136, which is 34. By the definition of a magic square, the sum of the numbers in each column and each diagonal must also be 34.

In that way, we can even obtain a formula for the magic number of any n × n magic square. For this, we remind the reader of the discussion in chapter 4 about the sum of the first n natural numbers. Such a number is called a triangular number, T_n, and was determined by the formula

A magic square of size n × n contains all the natural numbers from 1 to n². Applying the formula above for this situation, we find that the sum of natural numbers from 1 to n² is

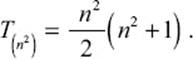
However, if it is required that each of the n rows must have the same sum, S_n, then the sum of each row must be

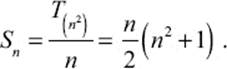
And, in a magic square, this number must be the sum of any row, column, or diagonal.

For n = 3, this formula indeed gives the magic number of the Lo Shu square:

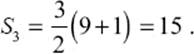
Here, we will consider magic squares consisting of all numbers from 1 to n², where n, the number of row or columns, is called the order of the magic square. However, if one adds a constant number k to all numbers in a magic square, one would obtain another magic square, with numbers ranging from k + 1 to k + n², and with magic number kn + S_n. Similarly, multiplying each number of a magic square with a constant k would give a magic square with magic number kS_n.

The question that would logically be asked is, how does one construct a magic square? How did Dürer come up with this special magic square? According to their order, we distinguish three types:

(1)magic squares of odd order (n is an odd number),

(2)magic squares of doubly-even order (n is a multiple of 4),

(3)magic squares of singly-even order (n is a multiple of 2, but not 4).

The Dürer magic square is a doubly-even magic square.