Numbers: Their Tales, Types, and Treasures.

Chapter 8: Special Numbers

8.8.THE MYSTICAL NUMBER 1,089

The number 1,089 has a number of oddities attached to it. One characteristic of this number can be seen by taking its reciprocal and getting the following:

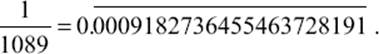
With the exception of the first three zeros and the last 1, we have a palindromic number—918,273,645,546,372,819—since it reads the same in both directions. Furthermore, if we multiply 1,089 by 5, we also get a palindromic number (5,445); and if we multiply 1,089 by 9, we get 9,801, the reverse of the original number. By the way, the only other number of four or fewer digits whose multiple is the reverse of the original number is 2,178, since 2,178 × 4 = 8,712.

Let us now do multiplication by 9 of some numbers that are modifications of 1,089—say 10,989; 109,989; 1,099,989; 10,999,989; and so on—and then marvel at the results:

10,989 × 9 = 98,901
109,989 × 9 = 989,901
1,099,989 × 9 = 9,899,901
10,999,989 × 9 = 98,999,901

and so on.

Returning to the number 1,089, we find that it has embedded in it a very entertaining oddity. Suppose you select any three-digit number whose units digit and hundreds digit are not the same, and then reverse that number. Now subtract the two numbers you have (obviously, the larger minus the smaller). Once again reverse the digits of this arrived-at difference, and add this new number to the difference. The result will always be 1,089.

To see how this works, we will choose any randomly selected three-digit number—say 732. We now subtract 732 – 237 = 495. Reversing the digits of 495, we get 594, and then we add these last two numbers: 495 + 594 = 1,089. Yes, this will hold true for all such three-digit numbers—amazing! This is a cute little “trick” that can be justified with simple algebra. We offer here an exercise in elementary algebra for the interested reader who is curious why this surprising trick works the way it does. We begin by representing an arbitrarily selected three-digit number, htu, as 100h + 10t + u, where h represents the hundreds digit, t represents the tens digit, and u represents the units digit (see chapter 1, section 12). The number with the digits reversed is then 100u + 10t + h. We will let h > u. Therefore, the original number is larger than the number with the reversed digits. Next, we subtract the reversed number uth from the original number htu (the minuend) with the usual algorithm, that is, by subtracting the digits at the units place. In this case, we have u – h < 0. Therefore, following the usual method of subtraction, we have to take 1 from the tens place (of the minuend), in order to make this subtraction possible. This makes the units place u + 10. Next, consider the subtraction at the tens place. The tens digits of the two numbers to be subtracted were equal, but now 1 was taken from the tens digit of the minuend, and the value of this digit became 10(t – 1). In order to enable subtraction in the tens place, 1 has to be taken away from the hundreds digit of the minuend. The hundreds digit of the minuend then becomes h – 1, making the value of the tens digit 10(t – 1) + 100 = 10(t + 9).

When we do the first subtraction, we actually subtract the two numbers in the following form:

Therefore the subtraction htu – uth gives

100(h – u – 1) + 10 × 9 + (u – h + 10).

Reversing the digits of this difference gives us

100(u – h + 10) + 10 × 9 + (h – u – 1).

By adding these last two expressions, we obtain

100(h – u – 1) + 10 × 9 + (u – h + 10) + 100(u – h + 10) + 10 × 9 + (h – u – 1) = 1000 + 90 – 1 = 1089.

This algebraic justification enables us to inspect the general case of this arithmetic process, thereby allowing us to guarantee that this process holds true for all numbers.