Numbers: Their Tales, Types, and Treasures.

Chapter 9: Number Relationships

9.5.FIBONACCI'S METHOD FOR FINDING PYTHAGOREAN TRIPLES

Fibonacci was perhaps one of the most influential mathematicians of the thirteenth century (chapter 6, section 1). In 1225, he published a book titled Liber quadratorum (Book of Squares), in which he demonstrated another relationship of numbers and stated the following:

I thought about the origin of all square numbers and discovered that they arise out of the increasing sequence of odd numbers; for the unity is a square and from it is made the first square, namely 1; that to this unity is added 3, making a second square, namely 4, with root 2; if to the sum is added the third odd number, namely 5, the third square is created, namely 9, with root 3; and thus sums of consecutive odd numbers and a sequence of squares always arise together in order.¹

Fibonacci was essentially describing the relationship that we discussed in chapter 4, section 4, that the sum of the first n odd numbers equals n²:

1 + 3 + 5 +…+ (2n – 1) = n².

We visualize this statement again in figure 9.3. Notice how the squares beginning with the single square at the lower left increase in area by the consecutive odd numbers analogous to what we just established algebraically. This is a geometric analogue of this algebraic statement.

Figure 9.3

Fibonacci knew of the Pythagorean theorem and therefore was aware of Pythagorean triples—after all, he lived about 1,700 years after Pythagoras. He was able to generate these triples in the following way. Let's consider the sum of the first five odd natural numbers (as shown in figure 9.3), 1 + 3 + 5 + 7 + 9 = 5², whose last term (9) is a square number. The sum in the parentheses: (1 + 3 + 5 + 7) + 9 = 5² is 16, which is also a square number because it is the sum of the first four odd numbers. So this equation can be rewritten as 16 + 9 = 25, which, surprisingly, gives us the primitive Pythagorean triple (3, 4, 5).

Let's consider another series of consecutive odd integers—one that ends with a square number—to convince ourselves that this scheme can really generate other primitive Pythagorean triples: Consider the sum of the first odd numbers up to the thirteenth, which happens to be a square number, 25 = 5²:

(1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23) + 25 = 169 = 13².

Using the same procedure as above, we add all the terms prior to the last one—within the parentheses. Because it is the sum of the first twelve odd numbers, it must be equal to the square number 12² = 144. Therefore, we obtain 144 + 25 = 169, or 12² + 5² =13². This gives us another primitive Pythagorean triple (5, 12, 13).

In general terms, Fibonacci's construction of Pythagorean triples can be described as follows: Choose any odd number a > 1. Every odd number has an odd square, therefore a² is also an odd number, and we can write it in the form a² = 2n + 1 for some natural number n. For example, we obtain a² = 9 for n = 4, which is the fifth odd number, and a² = 25 (for n = 12) is the thirteenth odd number. In general, 2n + 1 is the (n + 1)st odd number. Clearly, the sum of the first n + 1 odd numbers up to a² = 2n + 1 is equal to (n + 1)²:

1 + 3 + 5 +…+ (a² – 2) + a² = (n + 1)².

Here the summand (a² – 2) is the n^th odd number, and the sum of the odd numbers up to (a² – 2) is equal to n²:

1 + 3 + 5 +…+ (a² – 2) = n².

From this we obtain the following:

n² + a² = (n + 1)².

To summarize, for any odd number a, we can write a² = 2n + 1, and the triple (a, n, n + 1) is a Pythagorean triple. Curiously, it is even a primitive Pythagorean triple because the only common factor of n and n + 1 is 1. From a² = 2n + 1 we find and . We see that Fibonacci's method determines, for every odd number a = 3, 5, 7…, the primitive Pythagorean triple a, b = , c = . We can, therefore, conclude that there are an infinite number of primitive Pythagorean triples because there are infinitely many odd numbers. A few of these triples are listed in table 9.1.

We can further evaluate the numbers b_n in table 9.1 as

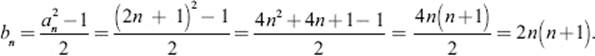
Therefore, Fibonacci's result means that

(a_n = 2n + 1, b_n = 2n(n + 1), c_n = 2n(n + 1) + 1)

is a primitive Pythagorean triple for all natural numbers n.

We also note that b_n = 4T_n, where is the nth triangular number defined in chapter 4, section 5. The sequence of triangular numbers starts with 1, 3, 6, 10, 15, 21, 28, 36…, and the b-values of table 9.1 are just four times these numbers. Therefore, Fibonacci's triples can also be written as (2k + 1, 4T_k, 4T_k + 1).

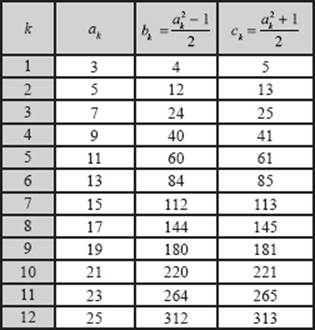
Table 9.1: Primitive Pythagorean triples obtained using Fibonacci's method.

Figure 9.4 shows the right triangles corresponding to the first eight Pythagorean triples in table 9.1. Because the hypotenuse differs from the longer leg by 1, these triangles tend to become rather long and extended.

Figure 9.4: Triangles corresponding to the Pythagorean triples in table 9.1.