Numbers: Their Tales, Types, and Treasures.

Chapter 1: Numbers and Counting

1.8.CARDINAL AND ORDINAL NUMBERS

The main ideas of the BOCIA principles are shown in figure 1.7. As we inspect them once again, we observe that numbers seem to play a double role.

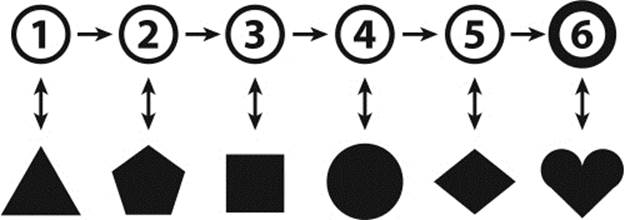
Figure 1.7: Counting principles.

· Any collection of arbitrary objects can be counted (abstraction principle). Figure 1.7 shows a collection of certain shapes.

· Counting is a process of associating unique “counting tags” with each of the objects. This one-to-one association between objects and counting tags is represented by the vertical double arrows (bijection principle).

· The counting tags must have a fixed order. In figure 1.7, the counting tags are simply the natural numbers 1, 2, 3, and so on, and their ordering is symbolized by the horizontal arrows.

· The act of counting puts the objects to be counted in a certain order, but the ordering of the objects is irrelevant (invariance principle). Rearranging the shapes would not change the final outcome.

· When we start counting at one, the cardinality (numerosity) of the set is described by the last of the number words (cardinal principle). The set of shapes in figure 1.7 has the cardinality six (a cardinal number).

As a first observation, we note that in the process of counting, number words are used in two different ways. On the one hand, number words tag the individual objects, giving them a certain order; on the other hand, one of these number words will denote the final result of counting and describe a property of the collection as a whole. The number words that serve as labels during counting represent ordinal numbers. Generally, ordinal numbers denote the position of an element in an ordered sequence. This is a very important concept, and on some occasions we use special number words for indicating an ordering, like first, second, third,…, seventeenth, and so on. Typically when we ask “which one?” or “which position?” the answer would be an ordinal number (“object number two” or “the third man”).

While ordinal numbers describe the position in a sequence, cardinal numbers are used to describe the size of a collection. The cardinal number of a collection is given by the number word obtained when, during counting, we reach the last object of the collection. This is the final result of the counting process. It represents what we called the numerosity, or cardinality, of a set. Whenever we ask “how many?” the typical answer will be a cardinal number (such as “five”).

In everyday life, you will frequently encounter a third type of numbers. These are called nominal numbers, and they just represent names, like telephone numbers or zip codes or item numbers in a catalog. A nominal number does not describe a size or quantity and need not imply any natural order. It is just for naming things and cannot be used in arithmetic operations. Certainly, it is of minor interest to mathematicians.

In order to appreciate the distinction between cardinality and ordinality, assume a moment that you have to relearn counting using letters of the alphabet instead of using numbers. Most probably, you will know already how to recite the sequence of twenty-six letters of the (English) alphabet in the correct order (A, B, C,…), hence you will certainly master the mechanical procedure of “counting” sets of up to twenty-six elements with letters instead of numbers. That means that you have mastered the ordinal principle, but probably not the cardinal principle. You can easily check your understanding of cardinality with the following questions: Do you have an intuitive feeling for the “number K”; that is, do you have an understanding of the size of a set containing K elements? Can you estimate the weight of F apples? And how large is a set that is F objects smaller than a set with K objects? Unless you have special training, it will not be easy to give the answer without resorting to counting with fingers. This is how it feels when you know how to count but still can't properly associate number words with cardinalities: You can't perform even simple computations without using your fingers.