Numbers: Their Tales, Types, and Treasures.

Chapter 9: Number Relationships

9.8.EXPLORING PYTHAGOREAN TRIPLES

Euclid's formula will allow us to discover many other relationships that exist among these Pythagorean triples. For example, when we inspect the values of m and n that determine a primitive Pythagorean triple and, in addition, where n = 1 (corresponding to the row of triangles at the bottom of figure 9.6), we notice that in table 9.3, the hypotenuse c (that is, the third member of the triple) will differ from one of the legs by 2.

Algebraically, this is easily demonstrated. Once again, consider the formula for generating all Pythagorean triples: a = m² – n², b = 2mn, and c = m² + n². When n = 1, we get a = m² – 1, b = 2m, c = m² + 1. Therefore, the difference between c and a is c – a = (m² + 1) – (m² – 1) = 2. Table 9.3 shows a few cases of primitive Pythagorean triples where n = 1.

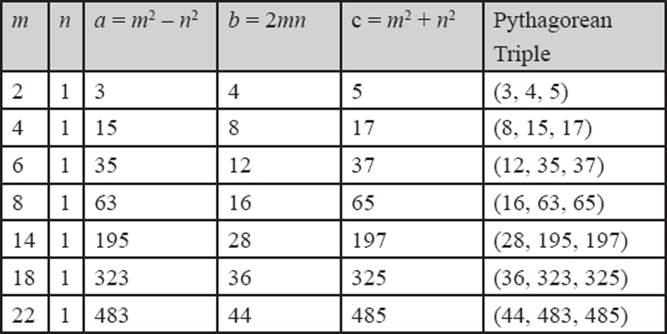
Table 9.3: Some primitive triples with n = 1.