Numbers: Their Tales, Types, and Treasures.

Chapter 9: Number Relationships

9.9.CONSECUTIVE MEMBERS OF A PYTHAGOREAN TRIPLE

The special Pythagorean triples, found by Fibonacci's method in table 9.1, all have the property that c = b + 1. For which values of m and n will this be the case? Inspection of the various values listed in table 9.2 reveals that when m – n = 1, then c – b = 1. By now it should be relatively easy to justify this finding algebraically. Indeed, we have

c – b = m² + n² – 2mn = (m – n)².

You can see that c – b = 1 in exactly the cases where (m – n)² = 1. This leads us to m – n = 1, or m – n = –1. However, m – n cannot be negative, since we always assume m > n. Therefore, the condition c – b = 1 is equivalent with m – n = 1, or m = n + 1. This verifies our conjecture about the difference of c – b = 1. All Pythagorean triples (a, b, c) with c – b = 1 have m – n = 1.

We can now ask whether there are some Pythagorean triples with the property c – b = 1 that are not among those obtained by Fibonacci's method. In order to answer this question, we apply Euclid's formula, which is known to give all Pythagorean triples. Because we know that any triple with c – b = 1 must have m – n = 1, we consider Euclid's formula with consecutive natural numbers n and m = n + 1, and find

a = m² – n² = (n + 1)² – n² = 2n + 1,
b = 2mn = 2(n + 1)n,
c = m² + n² = (n + 1)² + n² = 2n² + 2n + 1 = b + 1.

But this is precisely the formula (a = 2n + 1, b = 2n(n + 1), c = b + 1) for the Pythagorean triples constructed by Fibonacci's method that we obtained in section 5. Fibonacci's method already provided us with all triples with the property c – b = 1.

When we further inspect the list of Pythagorean triples in table 9.1, we notice not only that c = b + 1, but also that a² = b + c, a truly remarkable pattern among Pythagorean triples. For example, for the Pythagorean triple (7, 24, 25) we have 25 = 24 + 1, and at the same time we also have 7² = 24 + 25 = 49. This result follows easily from the formulas above:

a² = (2n + 1)² = 4n² + 4n + 1 = 4n(n + 1) + 1 = 2n(n + 1) + (2n(n + 1) + 1) = b + c.

While we are considering number relationships, we ought to consider a peculiarity among the b terms (i.e., 2mn) in this pattern-rich list shown in table 9.1, namely, 4, 12, 24, 40, 60, 84…. They just happen to fold nicely into the following pattern:

Searching for patterns among the Pythagorean triples can be a lot of fun. For example, perhaps the most obvious pattern to consider is that in which the three numbers of the triple are consecutive numbers, such as (3, 4, 5). To search for such triples, we can let the three members of the Pythagorean triple be represented by a = b – 1, b, c = b + 1. Now to secure them into the Pythagorean relationship we get:

(b – 1)² + b² = (b + 1)²,
b² – 2b + 1 + b² = b² + 2b + 1,
b² = 4b, therefore b = 4.

The resulting Pythagorean triple is then (3, 4, 5), where the three members are in consecutive order (i.e., each of the members differ by 1). This indicates to us that the Pythagorean triple (3, 4, 5) is the only Pythagorean triple where all three members are consecutive numbers.

But there are some Pythagorean triples that have two consecutive numbers as the first two numbers of the triple. Our most familiar Pythagorean triple, (3, 4, 5), already meets this criterion, since 3 and 4 are consecutive numbers. Table 9.4 lists some others.

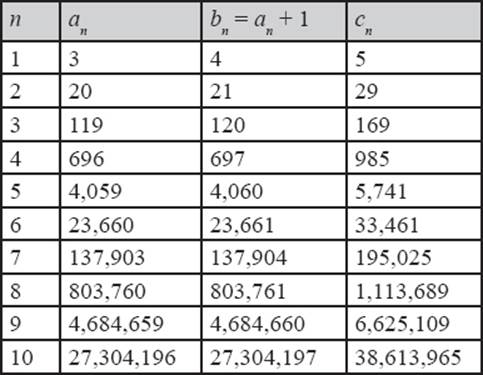
Table 9.4

Again if you search for it, a pattern can be found—as is so often the case in mathematics. However, this pattern is a bit different from earlier ones. The Pythagorean triple where the first two numbers are consecutive can be constructed as follows: Starting with a₁ = 3 and a₂ = 20, we obtain the third triple in table 9.4 with the formula a₃ = 6 a₂ – a₁ + 2 = 120 – 3 + 2 = 119. The general formula for the a-values in table 9.4 is

a_n = 6a_n–1 – a_n–2 + 2, for n = 3, 4, 5…

Once we know a_n, we get the other consecutive number b_n of the Pythagorean triple just by adding 1. The third member, c_n, can then be found by applying the Pythagorean relation, that is, by taking the square root of .