Numbers: Their Tales, Types, and Treasures.
Chapter 10: Numbers and Proportions
10.10.THE “PI-RAMID”
Using again s = 230.36 m and h = 146.5 m, we compute half the circumference 2s of the base and its ratio with the height h of the pyramid. We obtain
2s : h = 3.14485.
This number is suspiciously close to π ≈ 3.14159. If the originally assumed height was about 15 cm higher, then this proportion would be exact. The deviation is larger than it was with the golden ratio, but 15 cm is still within the range of uncertainty when determining the original height of an eroded monument. Therefore we can be sure that the following hypothesis is fully compatible with the empirically measured dimensions of the Cheops pyramid:
Hypothesis 3: The Great Pyramid of Cheops is designed in such a way that
2s : h = π, or 4s = 2hπ,
that is, the circumference of the base equals the circumference of a circle whose radius is the height of the pyramid.
Again, this hypothesis has the problem that π was not known in ancient Egypt. We know about Egyptian mathematical knowledge, in particular, from the Rhind papyrus (about 1650 BCE). This is a collection of exercises concerning different mathematical problems that were important at that time. It also contains problems about the area of circles that were approximately computed by dividing its area into a number of square regions. The method effectively amounts to using an approximate value of 3.16 for π (while the value in the pyramid has a much higher precision). It is also clear from this source that the Egyptians had no idea of the proportionality between the area of a circle and the square of the radius. Obviously, the concept of π was unknown to the Egyptians of that era. How then is it possible that the number π is present in the pyramid with such “unreasonable” accuracy?
Moreover, how can it be that the golden ratio appears together with π in the dimensions of the pyramid? This is indeed a marvelous coincidence. In order to appreciate this, we should look again at the right triangle in figure 10.15, which is formed by the half-side of the base, the height of the pyramid, and its slant height. This triangle is a very good approximation of the proportions of the so-called Kepler triangle, shown in figure 10.17. The Kepler triangle is defined as a right triangle with hypotenuse c = ϕ and sides a = 1 and 
. In this case, the Pythagorean theorem, a2+ b2 = c2, is equivalent to the defining equation for the golden ratio: 1 + ϕ = ϕ2. This triangle demonstrates exactly the golden ratio according to Hypothesis 1. But it also has the number π hidden in its proportions. The reason is an amazing, but nevertheless purely accidental, similarity of the following two numerical values:
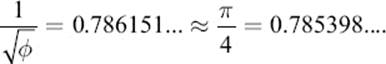
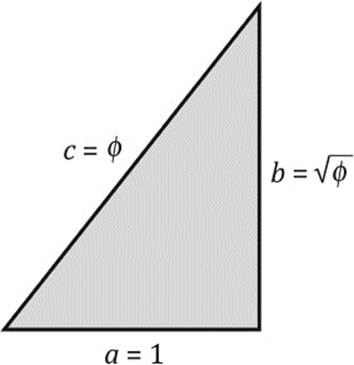
Figure 10.17: The Kepler triangle.
Because of this coincidence, the proportion of the legs of the Kepler triangle is related to π in the following way:
In the pyramid, this corresponds approximately to the proportion 
. For this reason, a pyramid that has ϕ in its proportions, has, in a very good approximation, also π in its proportions, and vice versa. Therefore, an explanation of Hypothesis 3 concerning the occurrence of π would at the same time explain Hypothesis 1 on the appearance of ϕ in the pyramid.
A very plausible explanation has been offered British physicist Kurt Mendelssohn (1906–1980) in his book The Riddle of the Pyramids. He assumes that horizontal distances were measured by the number of revolutions of a surveyor's wheel. In contrast, vertical distances would have to be measured with the diameter of the wheel as the unit of length, which we pictured in figure 10.18. Thus, the side of the base of the pyramid would correspond to a certain multiple of the circumference of the surveyor's wheel, while the height would correspond to a certain multiple of its diameter. In that way, the proportion π between circumference and diameter of the wheel would be included in the proportions of the pyramid without the Egyptians having been aware of it.
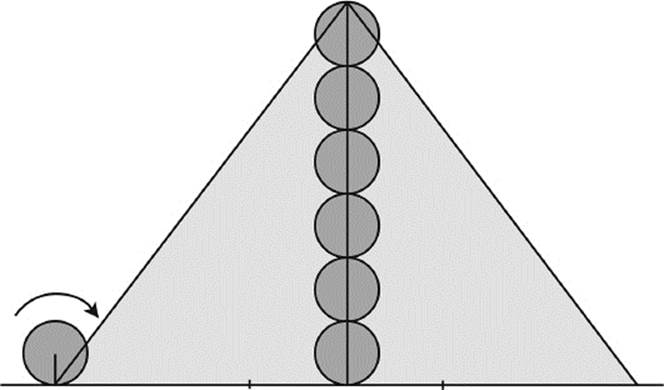
Figure 10.18: Surveyor's wheel for measuring lengths and heights.
Unfortunately, this explanation has not been supported scientifically. While there are ancient pictures showing Egyptians handling instruments, there is no hint that they could have used wheels for measuring lengths. The assumption has no other justification than to explain the occurrence of the number π in the Great Pyramid, as we have done here. If one could come up with a simpler explanation, it would be preferred over any assumption of a forgotten knowledge about higher geometry. Indeed, such an explanation exists.