Pre-Calculus For Dummies, 2nd Edition (2012)

Part II. The Essentials of Trigonometry

In this part . . .

Trigonometry is a subject that most students cover briefly in geometry. However, pre-calculus expands on those ideas. We begin with a review of angles and how to build the valuable tool known as the unit circle, based on previous knowledge of the special triangles. We examine right triangles and the basic trig functions built in them. Graphing trig functions may or may not be a review, depending on the Algebra II course you’ve taken, so we take the time to establish how to graph the parent graph of the six basic trig functions and then explain how to transform those graphs to get to the more complicated ones.

This part covers the often-feared and seldom-understood formulas and identities for trig functions. We break each identity down into more-manageable pieces. We show you how to simplify trig expressions and then how to solve trig equations for an unknown variable using formulas and identities. Lastly, we cover how to solve triangles that aren’t right triangles using the Law of Sines and the Law of Cosines.

Chapter 6. Circling in on Angles

In This Chapter

Discovering alternate trig function definitions

Placing angle measurements on a unit circle

In this chapter, we move on to right triangles drawn on the coordinate plane (x- and y-axes). Moving right triangles onto the coordinate plane brings out many more interesting concepts (such as evaluating trig functions and solving trig equations) that we look at in this chapter, all through a very handy tool known as the unit circle.

The unit circle is extremely important in the real world and in mathematics; for instance, you’re at its mercy whenever you fly in an airplane. Pilots use the unit circle, along with vectors, to fly airplanes in the correct direction and over the correct distance. Imagine the disaster that would result if a pilot tried to land a plane a bit to the left of the runway!

In this chapter, we work on building the unit circle together as we review the basics of angles in radians and triangles. With that information, you can place the triangles onto the unit circle (which is also located in the coordinate plane) to solve the problems we present at the end of this chapter. (We build on these ideas even further as we move into graphing trig functions in Chapter 7.)

Introducing Radians: Circles Weren’t Always Measured in Degrees

When you study geometry, you measure every angle in degrees, based on a portion of a 360° circle around the coordinate plane. As it turns out, the number 360 was picked to represent the degrees in a circle only for ­convenience.

What’s the convenience of the number 360, you ask? Well, you can divide a circle into many different, equal parts by using the number 360, because it’s divisible by 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45 . . . and these are just the numbers less than 50! Basically, the number 360 is pretty darn flexible for performing calculations.

The truth that not many people realize, though, is that degrees weren’t the first form of angle measurement — radians were. The word radian is based on the same root word as radius, which is the building block of a circle. An angle measurement of 360°, or a complete circle, is equal to 2π radians, which breaks down in the same way that degrees do.

In pre-calculus, you draw every angle with its vertex at the origin of the coordinate plane (0, 0), and you place one side on the positive x-axis (this side is called the initial side of the angle, and it is always in this location). The other side of the angle extends from the origin to anywhere on the coordinate plane (this side is the terminal side). An angle whose initial side lies on the positive x-axis is said to be in standard position.

If you move from the initial side to the terminal side in a counterclockwise direction, the angle has a positive measure. If you move from the initial side to the terminal side in a clockwise direction, you say that this angle has a negative measure.

A positive/negative discussion of angles brings up another related and important point: co-terminal angles. Co-terminal angles are angles that have different measures, but their terminal sides lie in the same spot. These angles can be found by adding or subtracting 360° (or 2π radians) from an angle as many times as you want. Infinitely many co-terminal angles exist, which becomes quite handy in future chapters!

Trig Ratios: Taking Right Triangles a Step Further

Reach back into your brain for a second and recall that a ratio is the comparison of two things. If a pre-calc class has 20 guys and 14 girls, the ratio of guys to girls is 20/14, and because that’s a fraction, the ratio reduces to 10/7. Ratios are important in many areas of life. For instance, if you have 20 people at a cookout with only 10 burgers, the ratio tells you that you have a problem!

Because you spend a ton of time in pre-calc working with trigonometric functions, you need to understand ratios. In this section, we look at three very important ratios in right triangles — sine, cosine, and tangent — as well as three not-so-vital but still important ratios — cosecant, secant, and cotangent. These ratios are all functions, where an angle is the input, so some textbooks use the words trig function and trig ratio interchangeably. Each function looks at an angle of a right triangle, known or unknown, and then uses the definition of its specific ratio to help you find missing information in the triangle quickly and easily. To round out this section, we show you how to use inverse trig functions to solve for an unknown angle in a right triangle.

You can remember the trig functions and their definitions by using the ­mnemonic device SOHCAHTOA, which stands for

Sine = Opposite over hypotenuse

Cosine = Adjacent over hypotenuse

Tangent = Opposite over adjacent

Making a sine

The sine of an angle is defined as the ratio of the opposite leg to the hypotenuse. In symbols, you write sin θ. Here’s what the ratio looks like:

In order to find the sine of an angle, you must know the lengths of the opposite side and the hypotenuse. You will always be given the lengths of two sides, but if the two sides aren’t the ones you need to find a certain ratio, you can use the Pythagorean theorem to find the missing one. For example, to find the sine of angle F (sin F) in Figure 6-1, follow these steps:

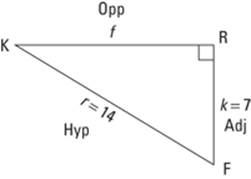
1. Identify the hypotenuse.

Where’s the right angle? It’s , so side r, across from it, is the hypotenuse. You can label it “Hyp.”

2. Locate the opposite side.

Look at the angle in question, which is here. Which side is across from it? Side f is the opposite leg. You can label it “Opp.”

3. Label the adjacent side.

The only side that’s left, side k, has to be the adjacent leg. You can label it “Adj.”

4. Locate the two sides that you use in the trig ratio.

Because you are finding the sine of , you need the opposite side and the hypotenuse. For this triangle, (leg)² + (leg)² = (hypotenuse)² becomes f² + k² = r². Plug in what you know to get f² + 7² = 14². When you solve this for f, you get .

5. Find the sine.

With the information from Step 4, you can find that

which reduces to

Looking for a cosine

The cosine of an angle, or cos θ, is defined as the ratio of the adjacent leg to the hypotenuse, or

Consider this example: A ladder leans against a building, creating an angle of 75° with the ground. The base of the ladder is 3 feet away from the building. How long is the ladder? Did your heart just sink when you realized we’re giving you a . . . word problem? No problem! Just follow these steps to solve; here, you’re looking for the length of the ladder:

1. Draw a picture so you can see a familiar shape.

Figure 6-2 represents the ladder leaning against the building.

The right angle goes between the building and the ground, because otherwise the building would be crooked and fall down. Because you know where the right angle is, you know that the hypotenuse is the ladder itself. The given angle is down on the ground, which means the opposite leg is the distance on the building from where the ladder touches to the ground. The third side, the adjacent leg, is the distance the ladder rests from the building.

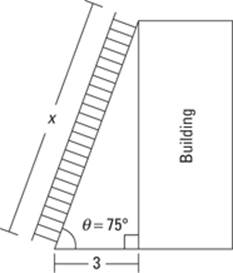
2. Set up a trigonometry equation, using the information from the picture.

You know that the adjacent side is 3 feet, and you’re looking for the length of the ladder, or the hypotenuse. Therefore, you have to use the cosine ratio, because it’s the ratio of the adjacent leg to the hypotenuse.

You have . The building has nothing to do with this problem

right now, other than it’s what’s holding up the ladder.

Why do you use 75° in the cosine function? Because you actually know how big the angle is; you don’t have to use θ to represent an unknown angle.

3. Solve for the unknown variable.

Multiply the unknown x to both sides to get xcos 75° = 3. The cos 75° is just a number. When you plug it into your calculator, you get a decimal answer (make sure you set your calculator to degree mode before attempting to do this problem). Now divide both sides by cos 75° to

isolate x; you get . This equation produces the answer ,

which means the ladder is about 11.6 feet long.

Going on a tangent

The tangent of an angle, or tan θ, is the ratio of the opposite leg to the adjacent leg. Here’s what it looks like in equation form:

Imagine for a moment that you’re an engineer. You’re working with a 39-foot tower with a wire attached to the top of it. The wire needs to attach to the ground and make an angle of 80° with the ground to keep the tower from moving. Your task is to figure out how far from the base of the tower the wire should attach to the ground. Follow these steps:

1. Draw a diagram that represents the given information.

Figure 6-3 shows the wire, the tower, and the known information.

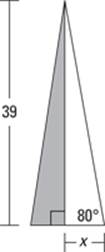
2. Set up a trigonometry equation, using the information from the picture.

For this problem, you must set up the trig equation that features tangent, because the opposite side is the length of the tower, the hypotenuse is the wire, and the adjacent side is what you need to find.

You get .

3. Solve for the unknown.

Multiply both sides by the unknown x to get xtan 80° = 39. Divide both

sides by the tan 80° to get . Simplify to get . The wire

attaches to the ground about 6.88 feet from the base of the tower to form the 80° angle.

Discovering the flip side: Reciprocal trig functions

Three additional trig ratios — secant, cosecant, and cotangent — are called reciprocal functions because they’re the reciprocals of sine, cosine, and tangent. These three functions open up three more ways in which you can solve equations in pre-calculus. The following list breaks down these functions and how you use them:

Cosecant, or csc θ, is the reciprocal of sine. The reciprocal of a is 1/a, so

Because

,

we see that

In other words, cosecant is the ratio of the hypotenuse to the opposite leg.

Secant, or sec θ, is the reciprocal of cosine. It has a formula similar to cosecant:

Secant, in other words, is the ratio of the hypotenuse to the adjacent leg.

A common mistake is to think that secant is the reciprocal of sine and that cosecant is the reciprocal of cosine, but the previous Bullet1s illustrate the truth.

Cotangent, or cot θ, is the reciprocal of tangent. (How’s that for ­obvious?) You have the hang of this if you’ve looked at the previous ­bullets:

Tan θ may also be written as

Therefore, cot θ may be written as the reciprocal — in other words,

Secant, cosecant, and cotangent are all reciprocals, but you won’t find a button for them on your calculator. You must use their reciprocals — sine, cosine, and tangent. Don’t get confused and use the sin^–1, cos^–1, and tan^–1 ­buttons, either. Those buttons are for inverse trig functions, which we describe in the following section.

Working in reverse: Inverse trig functions

Almost every function has an inverse. An inverse function basically undoes a function. The trigonometry functions sine, cosine, and tangent all have inverses, and they’re often called arcsin, arccos, and arctan.

In trig functions, theta (θ) is the input, and the output is the ratio of the sides of a triangle. If you’re given the ratio of the sides and need to find an angle, you must use the inverse trig function:

Inverse sine (arcsin):

Inverse cosine (arccos):

Inverse tangent (arctan):

Here’s what an inverse trig function looks like in action. To find the angle θ in degrees in a right triangle if the tan θ = 1.7, follow these steps:

1. Isolate the trig function on one side and move everything else to the other.

This step is done already. Tangent is on the left and the decimal 1.7 is on the right: tan θ = 1.7.

2. Isolate the variable.

You’re given the ratio for the trig function and have to find the angle. To work backward and figure out the angle, use some algebra. You have to undo the tangent function, which means using the inverse tangent function on both sides: tan^–1(tan θ) = tan^–1(1.7). This equation simplifies to θ = tan^–1(1.7).

3. Solve the simplified equation.

θ = tan^–1(1.7) gives you θ = 59.53°.

Read the problem carefully so you know whether the angle you’re looking for should be expressed in degrees or radians. Set your calculator to the correct mode.

Understanding How Trig Ratios Work on the Coordinate Plane

The unit circle that we build in this chapter lies on the coordinate plane — the same plane you’ve been graphing on since algebra. The unit circle is a very small circle centered at the origin (0, 0). The radius of the unit circle is 1, which is why it’s called the unit circle. To carry out the work of this chapter, all the angles specified need to be drawn on the coordinate plane, so we have to redefine the SOHCAHTOA ratios from earlier to make sense of them on the coordinate plane and the unit circle.

To put angles on the coordinate plane, essentially all you do is look at the trig ratios in terms of x and y values rather than opposite, adjacent, and hypotenuse. Redefining these ratios to fit the coordinate plane (sometimes called the point-in-the-plane definition) makes visualizing the differences easier. Some of the angles, for instance, are larger than 180°, but using the new definitions allows you to make a right triangle by using a point and the x-axis. You then use the new ratios to find missing sides of right triangles and/or trig function values of angles.

When a point (x, y) exists on a coordinate plane, you can calculate all the trig functions for the point by following these steps:

1. Locate the point on the coordinate plane and connect it to the origin, using a straight line.

Say, for example, that you’re asked to evaluate all six trig functions of the point in the plane (–4, –6). The line segment moving from this point to the origin is your hypotenuse and is now called the radius r (see Figure 6-4).

2. Draw a perpendicular line connecting the given point to the x-axis, creating a right triangle.

The legs of the right triangle are –4 and –6. Don’t let the negative signs scare you; the lengths of the sides are still 4 and 6. The negative signs just reveal the location of that point on the coordinate plane.

3. Find the length of the hypotenuse r by using the distance formula or the Pythagorean theorem.

The distance you want to find is the length of r from Step 1. Using the

distance formula between (x, y) and the origin (0, 0), you get .

This equation implies the principal or positive root only, so the hypotenuse for these point-in-the-plane triangles is always positive.

For our example, you get , which simplifies to . Check out what our triangle looks like in Figure 6-4.

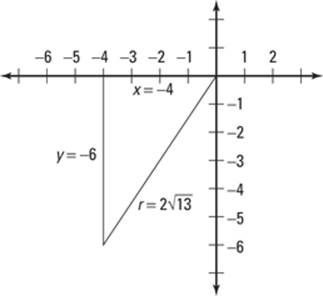
4. Evaluate the trig function values, using their alternate definitions.

With the labels from Figure 6-4, you get the following formulas:

• sin θ = y/r implies that csc θ = r/y.

• cos θ = x/r implies that sec θ = r/x.

• tan θ = y/x implies that cot θ = x/y.

Substitute the numbers from our example to pinpoint the trig values:

•

Simplify first:

Then rationalize the denominator:

•

Simplify first:

Then rationalize:

• tan θ = –6/–4

This answer simplifies to 3/2.

• cot θ = 2/3

•

•

Notice that the rules of trig functions and their reciprocals still apply. For example, if you know sin θ, you automatically know csc θ because they’re reciprocals.

When the point you’re given is a point on one of the axes, you can still find all the trig function values. For instance, if the point is on the x-axis, the cosine and the radius have the same absolute value (because the cosine can be negative but the radius can’t). If the point is on the positive x-axis, the cosine is 1 and the sine is 0; if the point is on the negative x-axis, the cosine is –1. Similarly, if the point is on the y-axis, the sine value and the radius are of the same absolute value; the sine will be either 1 or –1, and the cosine will always be 0.

Building the Unit Circle by Dissecting the Right Way

The unit circle is a vital part of the study of trigonometry. To visualize the tool, imagine a circle drawn on the coordinate plane, centered at the origin. The trig functions sine, cosine, and tangent rely heavily on the shortcuts that you can figure out by using the unit circle. It may be a new idea, but don’t be intimidated; the circle is simply built off concepts from geometry. In the following sections, we dissect the unit circle and use special right triangles to build it, which will be imperative to your studies in pre-calc.

Familiarizing yourself with the most common angles

In pre-calculus, you often need to draw an angle on the coordinate plane in order to make certain calculations. But we don’t recommend that you memorize where all the angles’ terminal sides lie in the unit circle, because that’s a waste of your time. Of course, because the 30° angle, the 45° angle, and the 60° angle are so common in pre-calc problems, dedicating to memory exactly where their terminal sides lie isn’t a bad idea. This information gives you a good foundation for figuring out where the rest of the unit-circle angles lie. These angles help you find the trig function values for those special (or more common) angles on the unit circle. And in Chapter 7, these special values help you graph the trig functions.

Figure 6-5 shows the 30°, 45°, and 60° angles.

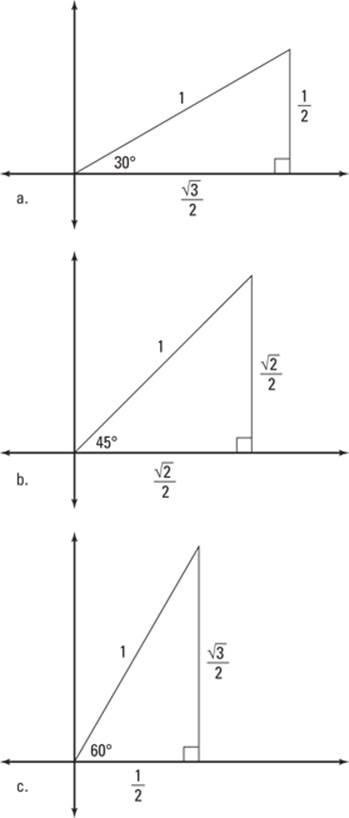
Instead of memorizing the locale of all the major angles on the unit circle, let the quadrants be your guide. Remember that each quadrant contains 90° (or π/2 radians) and that the measures increase when you move counterclockwise around the vertex. With that information and a little bit of math, you can figure out the location of the angle you need.

Drawing uncommon angles

Many times in your journey through trig — actually, all the time — drawing a figure will help you solve a given problem (refer to any example problem in this chapter for an illustration of how to use a picture to help). Trig always starts with the basics of drawing angles, so that by the time you get to the problems, the actual drawing stuff is second nature.

Always draw a picture for any trig problem. We know many students who’ve raised their grades by following this very simple advice. Drawing a picture makes the information given to you more visual and enables you to picture what’s going on.

We help you draw these angles by sketching their terminal sides in the correct places. Then, by drawing a vertical line up or down to the x-axis, you can make right triangles that fit in the unit circle, with smaller angles that are more familiar to you.

What do you do if you’re asked to draw an angle that has a measure greater than 360°? Or a negative measure? How about both? We bet your head is spinning! No worries; this section gives you the steps.

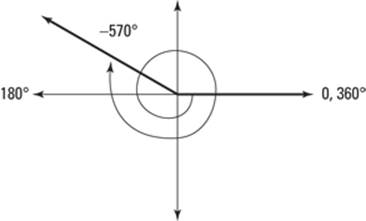
For example, suppose that you need to draw a –570° angle. Here’s what you do:

1. Find a co-terminal angle by adding 360°.

Adding 360° to –570° gives you –210°.

2. If the angle is still negative, keep adding 360° until you get a positive angle in standard position.

Adding 360° to –210° gives you 150°. This angle is 30° less than 180° (much closer to the 180° line than 90°).

3. Draw the angle you create in Step 2.

You need to draw a –570° angle, so be careful which way your arrow points and how many times you travel around the unit circle before you stop at the terminal side.

This angle starts at 0 on the x-axis and moves in a clockwise direction, because you’re finding a negative angle. Figure 6-6 shows what the finished angle looks like.

Digesting Special Triangle Ratios

You see two triangles over and over again in trigonometry; we call them the 45er and the old 30-60. In fact, you see them so often that most mathematicians recommend that you just memorize them. Relax! We show you how in this section. (And, yes, you’ve seen these triangles before in geometry.)

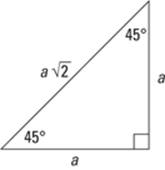
The 45er: 45°-45°-90° triangles

All 45°-45°-90° triangles have sides that are in a unique ratio. The two legs are the exact same length, and the hypotenuse is that length times . Figure 6-7

shows the ratio. (If you look at the 45er triangle in radians, you have . Either way, it’s still the same ratio.)

Why is this triangle important? Because any time you’re given one side of a 45er triangle, you can figure out the other two sides. When you complete ­calculations with this type of triangle, it will fall into one of two categories:

Type 1: You’re given one leg.

Because you know both legs are equal, you know the length of both the legs. You can find the hypotenuse by multiplying this length by .

Type 2: You’re given the hypotenuse.

Divide the hypotenuse by to find the legs (which are equal).

Here’s an example calculation: The diagonal in a square is 16 centimeters long. How long is each side of the square? Draw it out first. Figure 6-8 shows the square.

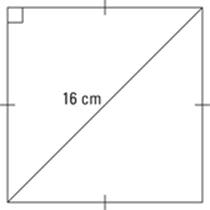
The diagonal of a square divides the angles into 45° pieces, so you have the hypotenuse of a 45er triangle. To find the legs, divide the hypotenuse by . When you do, you get .

You must now rationalize the denominator to get

which is the measure of each side of the square.

The old 30-60: 30°-60°-90° triangles

All 30°-60°-90° triangles have sides with the same basic ratio. If you look at the 30°-60°-90° triangle in radians, you see

The shortest leg is across from the 30° angle.

The length of the hypotenuse is always two times the length of the ­shortest leg.

You can find the long leg by multiplying the short leg by . (Don’t be scared, it’s just a square root sign; it won’t hurt you!)

Note: The hypotenuse is the longest side in a right triangle, which is different from the long leg. The long leg is the leg opposite the 60° angle.

Figure 6-9 illustrates the ratio of the sides for the 30-60-90 triangle.

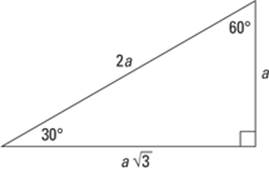
If you know one side of a 30-60 triangle, you can find the other two by using shortcuts. Here are the three situations you come across when doing these calculations:

Type 1: You know the short leg (the side across from the 30° angle): Double its length to find the hypotenuse. You can multiply the short side by to find the long leg.

Type 2: You know the hypotenuse: Divide the hypotenuse by 2 to find the short side. Multiply this answer by to find the long leg.

Type 3: You know the long leg (the side across from the 60° angle): Divide this side by to find the short side. Double that figure to find the hypotenuse.

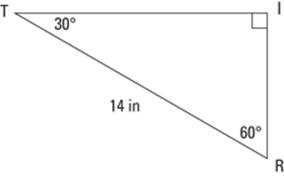
In the triangle TRI in Figure 6-10, the hypotenuse is 14 inches long; how long are the other sides?

Because you have the hypotenuse TR = 14, you can divide by 2 to get the short side: RI = 7. Now you multiply this length by to get the long side: IT = .

Triangles and the Unit Circle: Working Together for the Common Good

Rejoice in the fusion of right triangles, common angles (see the previous section), and the unit circle, because they come together for the greater good of pre-calculus! The special right triangles that we reviewed play an important role in finding specific trig function values that you can see on the unit circle. Specifically, if you know the measure of an angle, you can make a special right triangle that will fit onto the unit circle. Using this triangle, you can evaluate all kinds of trig functions without a calculator!

All congruent angles (angles with the same measure) have the same values for the different trig functions. Some noncongruent angles also have identical values for certain trig functions; you can use a reference angle to find out the measures for these angles.

Brush up on the special right triangles before attempting to evaluate the complicated functions in this section. Although many of the values look identical, looks can be deceiving. The numbers may be the same, but the signs and locations of these numbers change as you move around the unit circle.

Placing the major angles correctly, sans protractor

In this section, we take the unit-circle angles and the special right triangles and put them together to create a neat little package: the full unit circle. We create special triangles on the unit circle one at a time, because they’re all points on the coordinate plane.

Regardless of how long the sides are that make up a particular angle in a triangle, the trig function values for that specific angle are always the same. Therefore, mathematicians shrank all the sides of right triangles so that they’d all fit into the unit circle.

The hypotenuse of every triangle in a unit circle is always 1, and the calculations that involve the triangles are much easier to compute. Because of the unit circle, you can draw any angle with any measurement, and all right triangles with the same reference angle are the same size.

Starting in quadrant I: Calculate the points to plot

Look at an angle marked 30° in the unit circle (see Figure 6-11) and follow these steps to build a triangle out of it — similar to the steps from the section “Understanding How Trig Ratios Work on the Coordinate Plane”:

1. Draw the angle and connect it to the origin, using a straight line.

The terminal side of a 30° angle should be in the first quadrant, and the size of the angle should be rather small. In fact, it should be one-third of the way between 0° and 90°.

2. Draw a perpendicular line connecting the point where the ray stops to the x-axis, creating a right triangle.

The triangle’s hypotenuse is the radius of the unit circle; one of its legs is on the x-axis; and the other leg is parallel to the y-axis. You can see what this 30°-60°-90° triangle looks like in Figure 6-11.

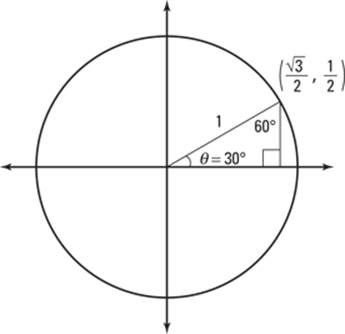
3. Find the length of the hypotenuse.

The radius of the unit circle is always 1, which means the hypotenuse of the triangle is also 1.

4. Find the lengths of the other sides.

To find the other two sides, you use the techniques we discuss in the 30°-60°-90° triangle section. Find the short leg first by dividing by 2,

which gives you 1/2. To find the long leg, multiply 1/2 by to get .

5. Identify the point on the unit circle.

The unit circle is on the coordinate plane, centered at the origin. So each of the points on the unit circle has unique coordinates. You can now

name the point at 30° on the circle: .

After going through the previous steps, you can easily find the points of other angles on the unit circle as well. For instance:

Look at the point on the circle marked 45°. You can draw a triangle from it, using Steps 1 and 2. Its hypotenuse is still 1, the radius of the unit circle. To find the length of the legs of a 45°-45°-90° triangle, you divide

the hypotenuse by . You then rationalize the denominator to get .

You can now name this point on the circle .

Moving counterclockwise to the 60° angle, you can create a triangle with Steps 1 and 2. If you look closely, you’ll realize that the 30° angle is at the top, so the short side is the side on the x-axis. That makes the point at

60° , due to the radius of 1 (divide 1 by 2 and multiply 1/2 by ).

Moving along to the other quadrants

Quadrants II–IV in the coordinate plane are just mirror images of the first quadrant (see the previous section). However, the signs are different because the points on the unit circle are on different locations of the plane:

In quadrant I, both x and y values are positive.

In quadrant II, x is negative and y is positive.

In quadrant III, both x and y are negative.

In quadrant IV, x is positive and y is negative.

The good news is that you never have to memorize the whole unit circle. You can simply apply the basics of what you know about right triangles and the unit circle! Figure 6-12 shows the whole pizza pie of the unit circle.

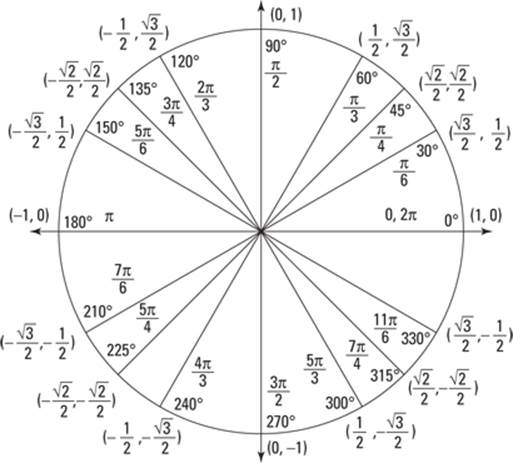
Retrieving trig-function values on the unit circle

You may be wondering why we spewed all this information about triangles, angles, and unit circles in the previous sections of this chapter. You need to be comfortable with the unit circle and the special triangles in it so that you can evaluate trig functions quickly and with ease, which you do in this section. You don’t want to waste precious moments during an exam constructing the entire unit circle just to evaluate a couple angles. And the more comfortable you are with trig ratios and the unit circle as a whole, the less likely you are to make an error with a negative sign or get trig values mixed up.

Finding values for the six trig functions

In pre-calc, you need to evaluate the six trig functions — sine, cosine, tangent, cosecant, secant, and cotangent — for a single value on the unit circle. For each angle on the unit circle, three other angles have similar trig function values. The only difference is that the signs of these values are opposite, depending on which quadrant the angle is in. Sometimes the angle won’t be on the unit circle and you’ll have to use your calculator.

If you don’t have the unit circle at your disposal (if you’re taking a test, for instance), you can draw a picture and find the values you need the long way, which we explain in this section. (However, as you progress, you’ll discover a shortcut you can use to simplify the process, which we explain in the following section.)

The point-in-the-plane definition of cosine in a right triangle is cos θ = x/r. Because the hypotenuse r is always 1 in the unit circle, the x value is the cosine value. And if you remember the alternate definition of sine — sin θ = y/r — you’ll realize that the y value is the sine value. Therefore, any point anywhere on the unit circle is always (cos θ, sin θ). Talk about putting all the pieces together!

Alphabetically, x comes before y and c comes before s (cosine comes before sine, in other words). This fact should help you remember which one is which.

Tangent, cotangent, secant, and cosecant require a little more effort than the sine and cosine do. For many angles on the unit circle, evaluating these functions requires some careful work with fractions and square roots. Remember to always rationalize the denominator for any fraction in your final answer. Also, remember that any number divided by 0 is undefined. The tangent and secant functions, for instance, are undefined when the cosine value is 0. Similarly, the cotangent and cosecant values are undefined when the sine value is 0.

Time for an example. To evaluate the six trigonometric functions of 225° on the unit circle, follow these steps.

1. Draw the picture.

When you’re asked to find the trig function of an angle, you don’t have to draw out a unit circle every time. Instead, use your smarts to figure out the picture. For this example, 225° is 45° more than 180°. Draw out a 45°-45°-90° triangle in the third quadrant only (see the earlier section “Placing the major angles correctly, sans protractor”).

2. Fill in the lengths of the legs and the hypotenuse.

Use the rules of the 45er triangle. The coordinate of the point at 225° is

Figure 6-13 shows the triangle, as well as all the information to evaluate the six trig functions.

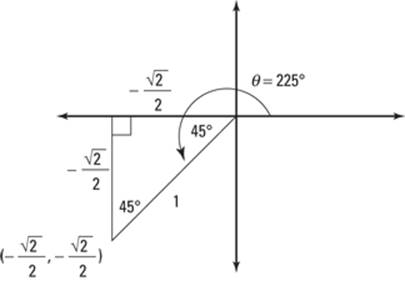
Be careful! Use what you know about the positive and negative axes on the coordinate plane to help you. Because the triangle is in the third quadrant, both the x and y values should be negative.

3. Find the sine of the angle.

The sine of an angle is the y value, or the vertical line that extends from the point on the unit circle to the x-axis. For 225°, the y value is

so sin(225°) = .

4. Find the cosine of the angle.

The cosine value is the x value, so it must be .

5. Find the tangent of the angle.

To find the tangent of an angle on the unit circle, you use the tangent’s alternate definition: tan θ = y/x. Another way of looking at it is that

because in the unit circle, the y value is the sine and the x value is the cosine. So if you know the sine and cosine of any angle, you also know the tangent. (Thanks, unit circle!) The sine and the cosine of 225° are both

Therefore, you can divide the sine by the cosine to get the tangent of 225°, which is 1.

6. Find the cosecant of the angle.

The cosecant of any angle is 1 over sin θ, or r/y, using the point-in-the-plane definition. Using what you determined in Step 1,

sin(225°) =

you can now divide 1 by :

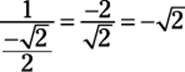
Hence, .

7. Find the secant of the angle.

The secant of any angle is 1 over cos θ. Because the cosine of 225° is also

,

found in Step 4, the secant of 225° is .

8. Find the cotangent of the angle.

The cotangent of an angle is 1 over tan θ. From Step 5, tan(225°) = 1. So cot(225°) = 1/1 = 1. Easy as pie!

The tangent is always the slope of the radius r. This easy calculation gives you a nice check for your work. Because the radius of the unit circle (the hypotenuse of the triangle) in the previous problem slants up, it has a positive slope, as does the tangent value.

The shortcut: Finding trig values of the 30°, 45°, and 60° families

Good news! We have a shortcut that can help you avoid the work of the previous section. You’ll have to do less memorizing when you realize that certain special angles (and, therefore, their special triangles) on the unit circle always follow the same ratio of the sides. All you have to do is use the quadrants of the coordinate plane to figure out the signs. Solving trig-function problems on the unit circle will be a blast after this section!

Perhaps you already figured out the shortcut by looking at Figure 6-12. If not, here are the families on the unit circle (for any family, the hypotenuse r is always 1):

The first family is the π/6 family (multiples of 30°). Any angle with the same denominator of 6 has these qualities:

• The longer leg is the x leg: .

• The shorter leg is the y leg: 1/2.

The second family is the π/3 family (multiples of 60°). Any angle with the same denominator of 3 has these qualities:

• The shorter leg is the x leg: 1/2.

• The longer leg is the y leg: .

The last family is the π/4 family (multiples of 45°). Any angle with the same denominator of 4 has this quality: The two legs are equal

in length: .

Finding the reference angle to solve for angles on the unit circle

A simple trig equation has a trig function on one side and a value on the other. The easiest trig equations to work are the ones where the value is a unit circle value, because the solutions come from the two special right triangles. However, in this section we start to express the solutions to trig equations in radians rather than degrees, simply for the sake of consistency. (Don’t worry; although the units you use to measure angles are different, the lengths of the sides still remain the same.) Radians show clear relationships between each of the families on the unit circle (see the previous section), and they’re helpful when finding a reference angle to solve for the solutions. (Radians are also the units used in graphing trig functions, which we cover in Chapter 7.)

Before pre-calc, you were asked to solve such algebraic equations as 3x² – 1 = 26. You learned to isolate the variable using inverse operations. Now you’re asked to do the same thing with trig functions in an attempt to find the value of the variable, which is now the angle that makes the equation true. After you find an angle that makes the equation true, you use that as the reference angle to find other angles on the unit circle that will also work in the equation. Usually you can find two, but you may find none, one, or more than two.

You can use your knowledge of trig functions to make an educated guess about how many solutions an equation can have. If the sine or cosine values are greater than 1 or less than –1, for instance, the equation has no solutions.

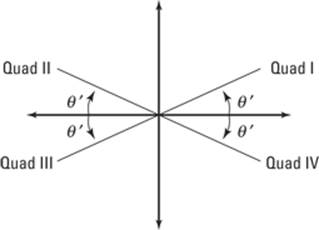
Using a reference angle to find the solution angle(s)

θ' (theta prime) is the name given to the reference angle, and θ is the actual solution to the equation, so you can find solutions by using the following quadrant rules, as seen in Figure 6-14:

QI: θ = θ' because the reference angle and the solution angle are the same.

QII: θ = π – θ' because it falls short of π by however much the reference angle is.

QIII: θ = π + θ' because the angle is greater than π.

QIV: θ = 2π – θ' because it falls short of a full circle by however much the reference angle is.

When you see a trig equation that asks you to solve for an unknown variable, you move backward from what you’re given to arrive at a solution that makes sense. This solution should be in the form of an angle measurement, and the location of the angle should be in the correct quadrant. Knowledge of the unit circle comes in handy here because you’ll be thinking of angles that fulfill the requirements of the given equation.

Suppose you’re asked to solve 2 cos x = 1. To solve, you need to think about which angles on the unit circle have cosine values that equal 1 when multiplied by 2. Follow these steps:

1. Isolate the trig function on one side.

You solve for cos x by dividing both sides by 2: cos x = 1/2.

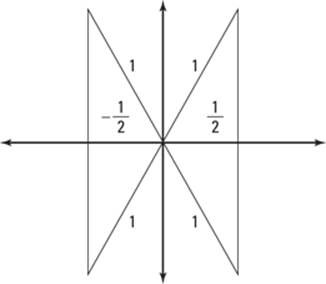
2. Determine which quadrants your solutions lie in.

Keeping in mind that cosine is an x value (see the earlier section “Finding values for the six trig functions”), you draw four triangles — one in each quadrant — with the x-axis legs labeled 1/2. Figure 6-15 shows these four triangles.

The two triangles on the left have a value of –1/2 for the horizontal leg, not 1/2. Therefore, you can eliminate them. Your solutions are in quadrants I and IV.

3. Fill in the missing leg values for each triangle.

You’ve already marked the x-axis legs. Based on knowledge of the unit circle and special triangles, you know that the side parallel to the y-axis

has to be and that the hypotenuse is 1. Figure 6-16 shows the two

labeled triangles.

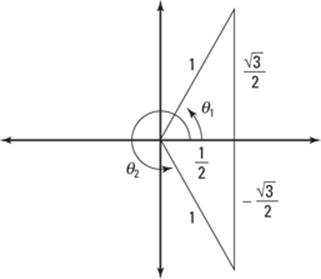
4. Determine the reference angle.

In the special right triangles, a side length of 1/2 is the short leg of a 30°-60°-90° right triangle. Therefore, the cosine (or the part along the x-axis) is the short leg and the vertical leg is the long leg. So the vertex of the angle at the center of the unit circle has a measure of 60°, making the reference angle π/3.

5. Express the solutions in standard form.

The reference angle is θ' = π/3. The first quadrant solution is the same as the reference angle: θ' = π/3. The fourth quadrant solution is θ = (2π) – θ' = (2π) – π/3 = (5π)/33.

Combining reference angles with other solving techniques

You can incorporate reference angles (see the previous section) into some other pre-calc techniques to solve trig equations. One such technique is factoring. You’ve been factoring since algebra (and in Chapter 4), so this process shouldn’t be anything new. When confronted with an equation that’s equal to 0 and a trig function that’s being squared, or you have two different trig functions that are being multiplied together, you should try to use factoring to get your solution first. After factoring, you can use the zero-product property (see Chapter 1) to set each factor equal to 0 and then solve them separately.

Try solving an example that involves factoring a trinomial — 2 sin² x + sin x – 1 = 0 — using the following steps:

1. Let a variable equal the trig ratio and rewrite the equation to simplify.

Let u = sin x and rewrite the equation as 2u² + u – 1 = 0.

2. Check to make sure that the equation factors.

Remember to always check for greatest common factor first. Refer to the factoring information in Chapter 4.

3. Factor the quadratic.

The equation 2u² + u – 1 = 0 factors to (u + 1)(2u – 1) = 0.

4. Switch the variables back to trig functions.

Rewriting your factored trig equation gives you (sin x + 1)(2 sin x – 1) = 0.

5. Use the zero-product property to solve.

If sin x = –1, x = (3π)/2; if sin x = 1/2, then x = π/6 and x = (5π)/6.

In pre-calc, you may be required to take the square root of both sides to solve a trig function. For example, if you’re given an equation such as 4 sin² x – 3 = 0, follow these steps:

1. Isolate the trig expression.

For 4 sin² x – 3 = 0, add 3 to each side and divide by 4 on both sides to get sin² x = 3/4.

2. Take the square root of both sides.

Don’t forget to take the positive and negative square roots, which gives

you sin x = ±.

3. Solve to find the reference angle.

The sine of x is both positive and negative for this example, which means that the solutions, or angles, are in all four quadrants. The positive solutions are in quadrants I and II, and the negative solutions are in quadrants III and IV. Use the reference angle in quadrant I to guide you to all four solutions.

If , the y value in the first quadrant is the long leg of the

30°-60°-90° triangle. Therefore, the reference angle is π/3.

4. Find the solutions.

Use the reference angle to find the four solutions:

• x = π/3

• x = (2π)/3

• x = (4π)/3

• x = (5π)/3

Note that two of these solutions come from the positive sign value and two come from the negative.

Measuring Arcs: When the Circle Is Put in Motion

Knowing how to calculate the circumference of a circle and, in turn, the length of an arc — a portion of the circumference — is important in pre-calc because you can use that information to analyze the motion of an object moving in a circle.

An arc can come from a central angle, which is one whose vertex is located at the center of the circle. You can measure an arc in two different ways:

As an angle: The measure of an arc as an angle is the same as the central angle that intercepts it.

As a length: The length of an arc is directly proportional to the circumference of the circle and is dependent on both the central angle and the radius of the circle.

If you think back to geometry, you may remember that the formula for the circumference of a circle is C = 2πr, with r standing for the radius. Also recall that a circle has 360°. So if you need to find the length of an arc, you need to figure out what part of the whole circumference (or what fraction) you’re looking at.

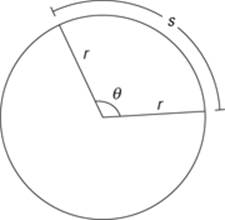
You use the following formula to calculate the arc length; θ represents the measure of the angle in degrees, and s represents arc length, as shown in Figure 6-17:

If the given angle is in radians, the 2π cancels and its arc length is

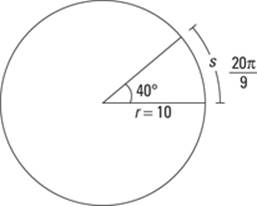
Time for an example. To find the length of an arc with an angle measurement of 40° if the circle has a radius of 10, use the following steps:

1. Assign variable names to the values in the problem.

The angle measurement here is 40°, which is θ. The radius is 10, which is r.

2. Plug the known values into the formula.

This step gives you

3. Simplify to solve the formula.

You first get

which multiplies to

Figure 6-18 shows what this arc looks like.

Now try a different problem. Find the measure of the central angle of a circle in radians with an arc length of 28π and a radius of 16. This time, you must solve for θ (the formula is s = rθ when dealing with radians):

1. Plug in what you know to the radian formula.

This gives you 28π = 16θ.

2. Divide both sides by 16.

Your formula looks like this:

3. Reduce the fraction.

You’re left with the solution: