Mathematics and the Real World: The Remarkable Role of Evolution in the Making of Mathematics (2014)
CHAPTER I. EVOLUTION, MATHEMATICS, AND THE EVOLUTION OF MATHEMATICS
4. MATHEMATICS THAT YIELDS AN EVOLUTIONARY ADVANTAGE
Mathematics has many aspects. The previous section showed that the ability to perform arithmetic calculations is the result of evolution. In this section we will indicate other branches of mathematical operations that, it may reasonably be assumed, provided an advantage in the evolutionary struggle. We will present evidence that those parts of mathematics were also incorporated in the genetic heritage. We may refer to this aspect of mathematics as natural mathematics. In the next section we will describe mathematical operations that are not natural, as they did not afford any evolutionary advantage in the hundreds of thousands of years during which the human genome was formed.
It is reasonable to assume that the ability to recognize geometrical elements gave an evolutionary advantage. As sources of food and water have typical geometric shapes, being able to recognize those shapes correctly constituted an advantage in the competition for sources of sustenance. But is there any evidence that, as a result of evolution, the recognition of geometric shapes is carried by the genes? We will soon turn our attention to such evidence but will first introduce what is known as the golden cut, or the golden-ratio rectangle.
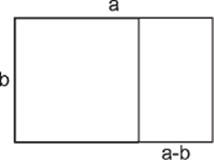
The golden-ratio rectangle is one in which the ratio between the longer side and the shorter side is such that if a square with sides the length of the shorter side of the rectangle is removed, the sides of the rectangle that remains will have the same ratio as the original one. We note, although this is not relevant to our tale, that it is not difficult to calculate the numerical value of the golden ratio (and skipping the calculation below will not impair the reader's understanding of what follows).
Denote the length of the rectangle by a, and the width by b. The relation required between the ratios is expressed by ![]() . If we denote by x the desired ratio
. If we denote by x the desired ratio ![]() , the unknown x satisfies the quadratic equation x2 – x = 1, the solution of which is (recalling secondary-school mathematics)
, the unknown x satisfies the quadratic equation x2 – x = 1, the solution of which is (recalling secondary-school mathematics) ![]() . This is the golden ratio, approximately 1.6180 in decimal numbers.
. This is the golden ratio, approximately 1.6180 in decimal numbers.
The golden ratio appears in many instances and processes in nature, and several of its attributes were known in ancient times. It has been identified in ancient architecture. For example, the dimensions of the Parthenon in Athens are amazingly close to those defined by the golden ratio. The ratio can also be discerned in Leonardo da Vinci's paintings; he also referred to it in his mathematical writings, although he did not state that he used it in his art.
The discovery of the golden ratio in various and sometimes-unexpected forms in nature resulted in the ancients attributing mystical properties to it, and they even referred to it as the divine proportion. For many years, a lively debate continued and is still continuing today among historians and artists on the question of whether builders and artists in ancient times made conscious use of the golden ratio in their architecture and art, or whether its frequent appearance is due to the fact that it is aesthetically pleasing. We will not join this open debate at this point but will just note that the ratio is indeed very pleasing to the eye. This has been proved in dozens of empirical studies, including studies showing that infants react with greater pleasure and calm to golden-ratio rectangles than they do to rectangles with other proportions, including those with greatly different proportions.
This needs to be explained. We are used to the fact that the pleasantness of a drawing or a painting or a shape to the adult eye is highly dependent on familiarity and education. For example, the attitude toward modern art initially was almost hostile, and it moderated over the years as the general public became more and more familiar with it. Babies have not had time to become familiar with any particular shape or form. What, then, is the origin of their preference for the golden ratio? The answer is simple: Evolution. An examination of the dimensions of the human head reveals that they are close to the golden ratio. Likewise, the proportions of sections of the human face, such as the ratio of the width and height of the eyes, the height and the width of the ears, and so on, are also close to the golden ratio. The evolutionary advantage to an infant who can recognize and is happy to discover a figure with those proportions is clear. Babies who are calm when they see their mother approaching, in contrast to exhibiting discomfort or even crying for help when they see a bird of prey nearby, have a greater chance of surviving. Hence the feeling of greater comfort when confronted with rectangular forms that have proportions similar to those of the human face rather than other forms is etched into the human genes. This has nothing to do with the golden ratio itself. In fact, research shows that babies also feel at ease with the shape of a hand, and the evolutionary reason for that is self-evident. Evolution rewards a baby who reacts with discomfort if held by a predator compared to its reaction when held by a human being. I would hazard a guess that if it were possible to perform similar experiments with birds, we would find that of all geometric forms, the most pleasing to a young chick would be an acute-angled triangle.
At this stage we may still wonder whether babies may have learned to feel comfortable with ratios similar to the golden ratio in the first weeks after their birth. The answer lies in the signs of discomfort and fear when they are faced with certain forms. Psychologists claim that about one-tenth of all children experience a primeval fear of clowns. Recently an occupation known as medical clowning has become widespread. It involves clowning activities meant to relax and help children requiring hospitalization. But cases have also been reported in which the activities of the medical clown only harmed the child, and the condition of the terrified children deteriorated when they saw the clown. This too is related to geometry and its evolutionary roots. The sight of a clown, with all his bright colors and the nonhuman proportion of his limbs and head, calls into play the same genes that make infants cry for their parents’ help when they see a multicolored bird of prey or a tiger approaching. It is unreasonable to think that in the modern world children would “learn” to be afraid of clowns. These innate features are the inception of geometric recognition. (We will often refer below to the simple but illustrative metaphor of confrontation with a tiger.)
Another basic mathematical ability that almost certainly played a role in the evolutionary struggle is the ability to identify patterns. I am not familiar with controlled experiments that show that the tendency and ability to recognize patterns is ingrained in the genes, but imagine early man with a tiger stealthily creeping up on him in the grass, leaving a trail of flattened grass. The ability to identify the trail as a source of danger could be life-saving. Ability to recognize patterns is not restricted to visual patterns. Consider for instance patterns of sound. For most of us, hearing very few notes is enough to recognize a pattern and sometimes to identify an entire tune or melody. As recognizing patterns is an attribute that is helpful in the evolutionary struggle, those who had this ability had more offspring than those that lacked it. It is thus almost certain that the tendency to recognize patterns is passed on genetically. Less harm is caused by seeing a pattern where none exists than by failure to identify an existing pattern. Thus, the evolutionary tendency to identify patterns also results in identifying ostensible patterns, including patterns that do not exist. We can take the Bible code as an instance of incorrect identification. By constructing sentences consisting of only every nth word of the text in the Bible, it can apparently be shown that many of the events in modern life were allegedly foreseen in the Old Testament. Careful statistical tests proved that these patterns have no scientific reality. From the outset, however, the tendency to find patterns overcame scientific caution. In later sections we will come across other mental errors deriving from discovering patterns where they do not exist.
Much of mathematics, both in research and in the various stages of learning mathematics, focuses on the identification of patterns in sequences. Here are a few simple exercises. Continue the sequence:
2, 4, 6, 8, 10,…
At a relatively early age, children will recognize the sequence of even numbers and will correctly give the next numbers in the sequence, 12 and 14. More knowledge is required to recognize the following sequence:
1, 4, 9, 16, 25, 36,…,
but it is not difficult to see that the numbers in the sequence are the squares of the numbers 1, 2, 3, 4, 5, 6, so that the following numbers will be 49 and 64. We should point out and emphasize that these sequences do not necessarily continue as we have suggested. In other words, these extensions of the sequences do not derive from a logical necessity. Moreover, the answers are culture dependent. Here is an exercise attributed to the mathematician and historian Morris Kline. Continue the sequence:
4, 14, 23, 34, 42, 50, 59,…
The answer? 72. The numbers in the sequence are the numbers of the streets at which the Manhattan Subway C stops, and the next station is at 72nd Street. I would guess that if regular travelers on the New York subway were given this exercise, many would have given the answer 72. I have deliberately avoided saying that they would have given the right answer, because this is not a matter of right and wrong. The answer is right if that is what the questioner intended. It is easy to see, however, that the human race has the inborn intuition to continue series such as the above in a reasonable manner, and to understand what the questioner wants. (We will discuss again this exercise in the last chapter of this book.)
Clearly one must not exaggerate, and the story of the four-engine airplane flying from New York to London comes to mind. About an hour after takeoff, the pilot announces that one of the four engines has failed, but there is nothing to worry about. The other three are working as they should, and the flight would just take nine hours instead of the originally scheduled six. A short while later the pilot announces that a second engine had ceased functioning, but not to worry, the only effect was that the flight would now take twelve hours. A while later comes the third announcement, that the third engine is now out of action, so the flight time is now fifteen hours. At this point a passenger jumps up and asks, “Is there enough food and drink on board in case the fourth engine fails and the flight takes eighteen hours?” (It would be interesting to ask mathematics students to complete the sequence in the event that the fourth engine stopped working.)
Some continuations of sequences, even if there is no logical necessity, are directly connected with natural phenomena. Let us take, for example, the following sequence:
1, 1, 2, 3, 5, 8, 13, 21,…
Each number (from the third) in the sequence is the sum of the previous two numbers, so that the next two in the sequence would be 34 and 55, and so on. This is the Fibonacci sequence, named after the Italian mathematician Leonardo Fibonacci, or Leonardo of Pisa (1170–1250), whose book Liber Abaci (1202) included extensive development of the properties of this sequence. It reflects many aspects of development and growth in nature, as well as mathematical properties that are interesting in themselves. We describe one use of the sequence here.
Certain trees, including some types of mangrove, increase in number by a branch taking root in the ground and growing into a new trunk. A year has to pass, however, until a branch of a young mangrove can send out one of its branches from which a new tree will grow. Assume that a young mangrove is planted in the ground. After one year there will still be one mangrove tree, but after two years a branch of the first tree will also be growing, so there will be two mangroves. This is the beginning of the sequence 1, 1, 2. The next year, only the first tree can send out a branch to take root, so in the fourth year there will be three trees. The year after that, the two oldest mangroves will send out a branch each, so there will be a total of 2 + 3 = 5 trees growing, and we already have the sequence 1, 1, 2, 3, 5, and so on. Each year the number of new trunks is equal to the number of older trees (more than a year old), and the sequence describing their number of trees is the Fibonacci sequence. We will not expand the scope of this matter beyond the example quoted, but I will just add that if a number in the sequence is divided by the preceding number, the further along the sequence we go, the closer is the result to the golden proportion discussed above. This is another fact that convinced the ancients that they were observing a divine proportion or ratio. The fact that series whose extensions can be discovered intuitively are reflected in natural phenomena boosted the tendency to develop the ability to identify patterns throughout the generations.
We will summarize the observations in this and the previous section by stating that we can point to, and to some extent corroborate by means of experiments, mathematical abilities that throughout hundreds of thousands of years of evolution afforded an advantage in the evolutionary struggle for survival. The processes of mutation and selection by which evolution shaped the human race resulted in those abilities being etched into human genes.