SAT SUBJECT TEST MATH LEVEL 1
TOPICS IN ARITHMETIC
CHAPTER 2
Basic Arithmetic
Exercises
1. ||–3| – |–4| – |–5|| =
(A) –2
(B) 2
(C) 4
(D) 6
(E) 12
2. What is the sum of the product and quotient of –5 and 5?
(A) –26
(B) –24
(C) –1
(D) 0
(E) 1
3. Which of the following statements are true?
I. The product of the integers from –5 to 4 is equal to the product of the integers from –4 to 5.
II. The sum of the integers from –5 to 4 is equal to the sum of the integers from –4 to 5.
III. The absolute value of the sum of the integers from –4 to 5 is equal to the sum of the absolute values of the integers from –4 to 5.
(A) I only
(B) III only
(C) I and II only
(D) I and III only
(E) I, II, and III
4. When the positive integer n is divided by 7, the remainder is 4. What is the remainder when n2 is divided by 7?
(A) 2
(B) 4
(C) 8
(D) 16
(E) It cannot be determined from the information given.
5. If 
, what is d in terms of a, b, and c?
(A) 
(B) c – a – b
(C) a + b – c
(D) c – ab
(E) 
6. What is the sum of the prime factors of 140?
(A) 7
(B) 9
(C) 12
(D) 14
(E) 15
7. Which of the following is the smallest integer that has a remainder of 1 when it is divided by 2, 3, 4, 5, 6, and 7?
(A) 61
(B) 141
(C) 211
(D) 421
(E) 841
8. What is the value of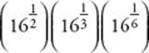 
?
(A) 1
(B) 
(C) 2
(D) 4
(E) 16
9. If x and y are positive integers, and (17x)y = 1717, what is the average (arithmetic mean) of x and y ?
(A) 
(B) 8.5
(C) 9
(D) 17
(E) It cannot be determined from the information given.
10. Which of the following equations have exactly one solution?
I. |x| = 1
II. x 2 = 1
III. 
= 1
(A) I only
(B) II only
(C) III only
(D) II and III only
(E) I, II, and III
11. For any integer n 
2, 
n
is defined to be the smallest prime factor of n. Which of the following is equal to 100 + 45?
(A) 10
(B) 15
(C) 35
(D) 50
(E) 135
12. Which of the following equations is equivalent to y = logb x ?
(A) y = bx
(B) x = by
(C) b = x y
(D) b = y x
(E) x = logby
13. 
(A) –1
(B) 0
(C) 1
(D) 2
(E) 7
14. Which of the following is equal to 
?
(A) 2
(B) 11
(C) 22
(D) 211
(E) 222
15. Which of the following are equal to 
for any real number a ?
I. a
II. 
III. |a|
(A) I only
(B) II only
(C) III only
(D) I and III only
(E) I, II, and III
ANSWERS EXPLAINED
Answer Key
|
1. (D) |
6. (D) |
11. (C) |
||
|
2. (A) |
7. (D) |
12. (B) |
||
|
3. (A) |
8. (E) |
13. (D) |
||
|
4. (A) |
9. (C) |
14. (C) |
||
|
5. (B) |
10. (C) |
15. (C) |
Solutions
Each of the problems in this set of exercises is typical of a question you could see on a Math 1 test. When you take the model tests in this book and, in particular, when you take the actual Math 1 test, if you get stuck on questions such as these, you don’t have to leave them out—you can almost always answer them by using one or more of the strategies discussed in the “Tactics” chapter. The solutions given here do not depend on those strategies; they are the correct mathematical ones.
See Important Tactics for an explanation of the symbol ⇒, which is used in several answer explanations.
1. (D) ||–3| – |–4| – |–5|| = |3 – 4 – 5| = |–6| = 6
2. (A) The product of 5 and –5 is (5)(–5) = –25. The quotient of 5 and –5 is (5) 
(–5) = –1. Their sum is (–25) + (–1) = –26.
3. (A) Since 0 is one of the integers from –5 to 4 and from –4 to 5, both products equal 0 (I is true). The sum of the integers from –5 to 4 is –5, whereas the sum of the integers from –4 to 5 is 5 (II is false). The absolute value of the sum of the integers from –4 to 5 is equal to the absolute value of 5, which is 5; the sum of the absolute values of each of the integers from –4 to 5 is 25 (III is false). Only statement I is true.
4. (A) The easiest solution is to choose an integer n that has a remainder of 4 when divided by 7, say n = 11. Then n2 = 121 = 7 
17 + 2. So the remainder is 2.
The correct mathematical solution is to note that by using KEY FACT A5, there is a positive integer q for which n = 7q + 4, and so
Since the expression in the final parentheses above is clearly divisible by 7, the remainder when n2 is divided by 7 is 2.
5. (B) (7a)(7b) = 7a+b, and 
.
Therefore, 
.
6. (D) 
. The prime factors of 140 are 2, 5, and 7. Their sum is 2 + 5 + 7 = 14.
7. (D) The LCM of 2, 3, 4, 5, 6, 7 is 420, so 420 is divisible by each of the integers from 2 to 7. Therefore, 421 will leave a remainder of 1 when divided by any of them.
8. (E)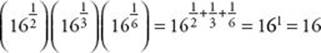 
9. (C) Since 1717 = (17x)y = 17xy, then xy = 17. The only positive integers whose product is 17 are 1 and 17.
Their average is 
.
10. (C) 
or x = –1 (I is false).
or x = –1 (II is false).
(III is true).
Only statement III is true.
11. (C) The smallest prime factor of 100 is 2, and the smallest prime factor of 45 is 3. So 100 + 45 = 2 + 3 = 5. Of the five choices, only 35 = 5.
12. (B) By KEY FACT A16, y = logbx if and only if b y = x.
13. (D) By KEY FACT A18, log7 1 = 0, log7 7 = 1, and 
. So
14. (C) By definition, log2 22 is the exponent to which 2 must be raised to equal 22. Therefore, .
15. (C) If a = –1, then 
. Of the three choices, only |–1| = 1. Only III is true.