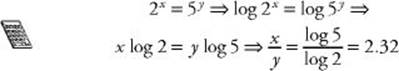SAT SUBJECT TEST MATH LEVEL 1
ALGEBRA
![]()
CHAPTER 6
Equations and Inequalities
![]()
EXPONENTIAL EQUATIONS
Sometimes on a Math 1 test you will have to solve an equation in which the variables are in the exponents. There are two ways to handle equations of this type: use the laws of exponents or use logarithms.
There is a big difference between the equations 2x–3 = 16 and 2x–3 = 15. The first equation is much easier to solve than the second if you recognize that 16 is a power of 2.
EXAMPLE 21: For what value of x is 2x–3 = 16?
![]()
EXAMPLE 22: For what value of x is 2x–3 = 15?
Since 15 is not a power of 2, you must use logarithms, which you evaluate on your calculator, to solve this equation. (See Chapter 2 to review the laws of logarithms.)
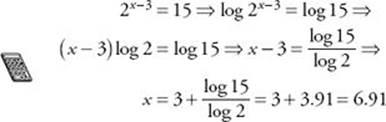
Of course, you could have used logarithms to solve the equation in Example 21. In that case, you would have
![]()
Smart Strategy
Only use logarithms if you have to.
Calculator Hint: Another option for solving exponential equations is to use a graphing calculator. For example, to solve the equation in Example 22, graph y = 2x–3, and trace along the curve until y = 15, zooming in to get any desired degree of accuracy.
|
TACTIC |
Use logarithms to solve equations in which variables appear in the exponents. |
Sometimes the exponents are on both sides of the equation. Again, if both sides can be written as powers of the same integer, you can use the laws of exponents.
Otherwise, you must use logarithms.
EXAMPLE 23:
![]()
EXAMPLE 24:
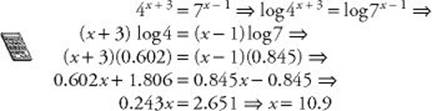
Note:
• In Example 23, 4 and 8 are both powers of 2, so you don”t need logarithms.
• In Example 24, 4 and 7 cannot be written as powers of the same integer, so you must use logarithms.
Occasionally, two different variables are in the exponents and you have to determine the relationship between the variables.
EXAMPLE 25: If 2x= 4y, what is the ratio of x to y ?
![]()
EXAMPLE 26: If 2x = 5y, what is the ratio of x to y ?