SAT SUBJECT TEST MATH LEVEL 1

ALGEBRA

CHAPTER 7
Word Problems

Exercises

1. How many seconds longer does it take to drive 1 mile at 40 miles per hour than at 60 miles per hour?

(A) 15

(B) 30

(C) 40

(D) 60

(E) 90

2. On Monday morning, Meri read part of her library book at a rate of 60 pages per hour. In the evening when she was tired, she read the same number of pages at a rate of 40 pages per hour. If Meri read for a total of two hours on Monday, how many minutes did she spend reading in the morning?

(A) 36

(B) 45

(C) 48

(D) 60

(E) 72

3. The product of two consecutive positive integers is 12 more than 12 times the sum of those two integers. What is the smaller of the two integers?

(A) 1

(B) 23

(C) 24

(D) 25

(E) 49

4. Charlie was 40 years old when his son Adam was born. How old was Charlie when he was 5 times as old as Adam?

(A) 40

(B) 45

(C) 50

(D) 60

(E) 80

5. If Mary can address a box of envelopes in 5 hours and Jane can address the same box of envelopes in 10 hours, how many minutes will it take Mary and Jane working together to address all the envelopes in the box?

(A) 80

(B) 160

(C) 200

(D) 450

(E) 900

6. Elaine has 50 coins, all nickels and dimes, that have a total value of $3.40. How many of her coins are nickels?

(A) 18

(B) 24

(C) 25

(D) 28

(E) 32

7. The length of each side of a square is 3 more than the length of each side of a regular pentagon. If the perimeters of the square and pentagon are equal, how long is each side of the pentagon?

(A) 6

(B) 12

(C) 10

(D) 15

(E) 18

8. At an amusement park, Lance bought 3 hamburgers and 4 sodas for a total of $15. While paying the same prices, Karen bought 2 hamburgers and 3 sodas for $10.50. What is the total cost of 1 hamburger and 1 soda?

(A) $1.50

(B) $3.00

(C) $4.00

(D) $4.50

(E) $5.00

ANSWERS EXPLAINED

Answer Key

Solutions

Each of the problems in this set of exercises is typical of a question you could see on a Math 1 test. When you take the model tests in this book and, in particular, when you take the actual Math 1 test, if you get stuck on questions such as these, you do not have to leave them out—you can almost always answer them by using one or more of the strategies discussed in the “Tactics” chapter. The solutions given here do not depend on those strategies; they are the correct mathematical ones.

See Important Tactics for an explanation of the symbol ⇒, which is used in several answer explanations.

1. (B) Since . The time required to drive 1 mile at 40 miles per hour

is (1.5) (60) seconds = 90 seconds.

The time required to drive 1 mile at 60 miles per hour is seconds. So it takes 90 – 60 = 30 seconds more to drive 1 mile at 40 miles per hour than at 60 miles per hour.

2. (C) Let d = the number of pages Meri read in the morning (and in the evening). Then let t₁ and t₂ be the times Meri spent reading in the morning and evening, respectively:

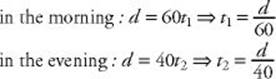
Since t₁ + t2 = 2, we have:

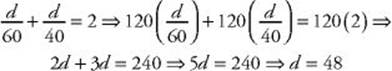
3. (C) Let n and n + 1 represent the two consecutive positive integers. Then:

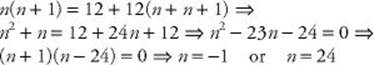
Since it is given that n is positive, n = 24.

4. (C) x years after Adam was born, Charlie was 40 + x years old and Adam was x years old.

So Charlie was 50 years old (and Adam was 10).

5. (C) Mary addresses envelopes at the rate of and Jane addresses envelopes at the rate of . Together they can address boxes per hour. So the whole job will take hours = 200 minutes.

6. (E) Let x represent the number of nickels Elaine has, and let y represent the number of dimes she has. Then x + y = 50. Since each nickel is worth 5 cents and each dime is worth 10 cents and since $3.40 is 340 cents: 5x + 10y = 340. Also,

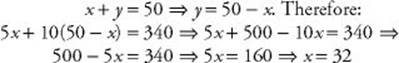
7. (B) Let x = the length of each side of the pentagon. Then x + 3 = the length of each side of the square. The perimeter of the pentagon is 5x and the perimeter of the square is 4(x + 3). Therefore:

8. (D) Let x = the cost of a hamburger, and let y = the cost of a soda. Then:

3x + 4y = 15

2x + 3y = 10.50

After multiplying the top equation by 3 and the bottom equation by 4, we get

9x + 12y = 45

8x + 12y = 42

Subtracting the second equation from the first gives us x = 3. Then substitute 3 for x:

So 1 hamburger and 1 soda cost 3 + 1.50 = $4.50.