SAT SUBJECT TEST MATH LEVEL 1
PLANE GEOMETRY
![]()
CHAPTER 8 Lines and Angles
![]()
• Angles
• Perpendicular and Parallel Lines
• Exercises
• Answers Explained
On the Math 1 test, approximately 20 of the 50 questions deal with geometry. Therefore, mastering geometry is crucial for anyone who is taking this test. Of the 20 geometry questions, about 10 of them are on plane geometry; the other 10 are split between solid geometry and coordinate geometry, which will be discussed in Chapters 12 and 13. Much of the geometry you have learned in your math classes is not covered on the Math 1 test. In this chapter, we will review all of the important topics in plane geometry that you need to know for the Math 1 test and only those.
Lines are usually referred to by lowercase letters, such as ![]() , m, and n. We can also name a line using two of the points on the line. If A and B are points on line
, m, and n. We can also name a line using two of the points on the line. If A and B are points on line ![]() , we can refer to line
, we can refer to line ![]() as line
as line ![]() .
.
![]() represents the ray that consists of point A and all the points on
represents the ray that consists of point A and all the points on ![]() that are on the same side of A as B.
that are on the same side of A as B.
![]() represents the line segment that consists of points A and B and all the points on
represents the line segment that consists of points A and B and all the points on ![]() that are between them.
that are between them.
Finally, AB represents the length of segment ![]() .
.
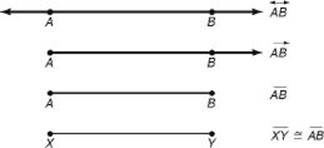
If two line segments have the same length, we say they are congruent. The symbol ![]() is used to indicate congruence, so in the figure below we have
is used to indicate congruence, so in the figure below we have ![]() .
.
TIP 
![]() the same thing as AB = XY.
the same thing as AB = XY.
ANGLES
An angle is formed by the intersection of two line segments, rays, or lines. The point of intersection is called the vertex of the angle. On the Math 1 test, angles are always measured in degrees and are classified according to their degree measures.
Key Fact G1
• An acute angle measures less than 90º
• A right angle measures 90º
• An obtuse angle measures more than 90º but less than 180º.
• A straight angle measures 180º.
Note
A small square drawn at the vertex of an angle is used to indicate that the angle is a right angle. On the Math Level 1 test, if an angle has a square in it, it must be a 90° angle, even if the figure has not been drawn to scale.
An angle can be named by three points: a point on one side, the vertex, and a point on the other side, in that order. When there is no possible ambiguity, we can name the angle just by its vertex.
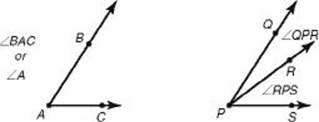
To indicate that the measure of angle A is 60°, say, we write m∠A = 60°.
Two angles that have the same measure are said to be congruent, denoted by the symbol ≅. So if m∠A = m∠B, we can write ∠A ≅ ∠B.
TIP 
∠A ≅ ∠B means the same thing as m∠A = m∠B
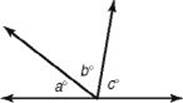
If the sum of the measures of two angles is 180°, we say that the angles are supplementary. If the sum of their measures is 90°, the angles are complementary. In the diagram below, ![]() is supplementary to
is supplementary to ![]() and
and ![]() is complementary to
is complementary to ![]() .
.
Key Fact G2
If two or more angles form a straight angle, the sum of their measures is 180º.
EXAMPLE 1: If in the figure below a : b : c = 2 : 3 : 4, then a = 2x, b = 3x, and c = 4x. So
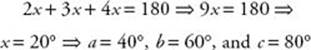
Key Fact G3
The sum of the measures of all nonoverlapping angles around a point is 360º.
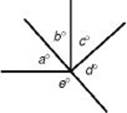
a + b + c + d + e = 360
When two lines intersect, four angles are formed. The two angles in each pair of opposite angles are called vertical angles.
Key Fact G4
Vertical angles have equal measures.
TIP 
Key Fact G4 means that vertical angles are congruent.
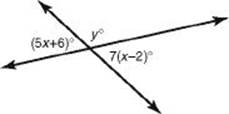
EXAMPLE 2: To find the value of y in the figure below, note that ![]() . Therefore, x = 10. So the measure of each acute angle is (5
. Therefore, x = 10. So the measure of each acute angle is (5 ![]() 10 + 6)° = 56° and y = 180 – 56 = 124.
10 + 6)° = 56° and y = 180 – 56 = 124.
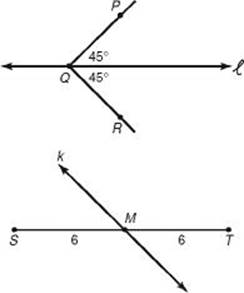
In the figure below, line ![]() divides
divides ![]() into two equal parts, and line k divides line segment
into two equal parts, and line k divides line segment ![]() into two equal parts. Line
into two equal parts. Line ![]() is said to bisect the angle, and line k bisects the line segment. Point M is called the midpoint of segment
is said to bisect the angle, and line k bisects the line segment. Point M is called the midpoint of segment ![]() .
.