SAT SUBJECT TEST MATH LEVEL 1
PLANE GEOMETRY
![]()
CHAPTER 8 Lines and Angles
![]()
PERPENDICULAR AND PARALLEL LINES
Two lines that intersect to form right angles are called perpendicular. Two lines that never intersect are said to be parallel. Consequently, parallel lines form no angles. However, if a third line, called a transversal, intersects a pair of parallel lines, eight angles are formed, and the relationships between these angles are very important.
Key Fact G5
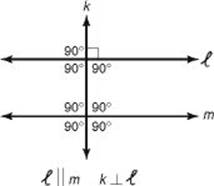
If a pair of parallel lines is cut by a transversal that is perpendicular to the parallel lines, all eight angles are right angles.
Key Fact G6
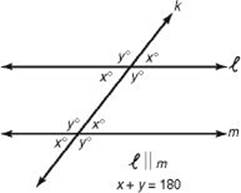
If a pair of parallel lines is cut by a transversal that is not perpendicular to the parallel lines:
• Four of the angles are acute, and four are obtuse.
• All four acute angles are congruent.
• All four obtuse angles are congruent.
• The sum of the measures of any acute angle and any obtuse angle is 180º.
TIP 
The four acute angles all have the same measure, and the four obtuse angles all have the same measure.
EXAMPLE 3: In the figure below, what is the value of a + b + c + d ?
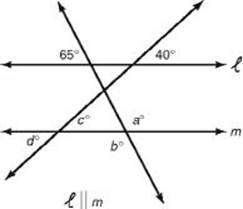
By KEY FACT G6, c and d each measure 40° and 65 + a = 180. Therefore, a = 115. Since vertical angles have equal measures, b is also 115, and so
a + b + c + d = 115 + 115 + 40 + 40 = 310.
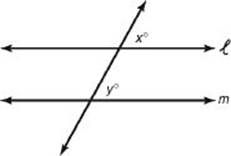
The converse of KEY FACT G6 is also true. If in the figure below, x = y, then lines ![]() and m are parallel.
and m are parallel.