SAT SUBJECT TEST MATH LEVEL 1

SOLID AND COORDINATE GEOMETRY

CHAPTER 12 Solid Geometry

• Rectangular Solids

• Cylinders

• Prisms

• Cones

• Pyramids

• Spheres

• Exercises

• Answers Explained

On a typical Math 1 test, there are about three questions on solid geometry. Most of them can be answered if you know the formulas for the volumes and surface areas of rectangular solids and cylinders. Although these formulas are given to you on the PSAT and SAT, they are not provided on the Math 1 test, so you must learn them.

Occasionally, a Math 1 test has one question about spheres, cones, or pyramids. The formulas you would need to answer such a question are given to you in a box labeled “Reference Information” at the beginning of the test. However, many Math 1 tests have no questions at all on these topics, so if your study time is limited, you may want to skip the discussion of these solids.

RECTANGULAR SOLIDS

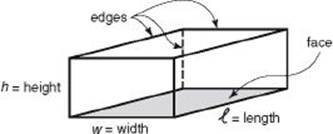
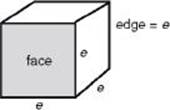
A rectangular solid or box is a solid formed by six rectangles, called faces. The sides of the rectangles are called edges. As in the diagram below, the edges are called the length, width, and height. A cube is a rectangular solid in which the length, width, and height are equal, so all the edges are the same length.

RECTANGULAR SOLID

CUBE

The volume of a solid is measured in cubic units. One cubic unit is the amount of space taken up by a cube all of whose edges are one unit long. In the figure on RECTANGULAR SOLIDS, if each edge of the cube is 1 inch, the area of each face is 1 square inch, and the volume of the cube is 1 cubic inch.

Key Fact K1

• The formula for the volume of a rectangular solid is V = wh, where , w, and h are the length, width, and height, respectively.

• Since all the edges of a cube are equal, if e is an edge, the formula for the volume of a cube is V = e³.

The surface area of a rectangular solid is the sum of the areas of the six rectangular faces. The areas of the top and bottom faces are equal, the areas of the front and The back faces are equal, and the areas of the left and right faces are equal. Therefore, to get the total surface area, we can calculate the area of one face from each pair, add them up, and then double the sum. In a cube, each of the six faces has the same area, so the surface area is six times the area of any face.

Key Fact K2

• The formula for the surface area of a rectangular solid is A = 2(w + h + wh).

• The formula for the surface area of a cube is A = 6e².

EXAMPLE 1: Assume that the surface area of a cube is x square inches, that the volume of that cube is y cubic inches, and that y = 2x. If the length of an edge of the cube is e inches, we have x = 6e ² and y = e³. Then

y = 2x e³ = 2(6e²) = 12e²

Dividing both sides of this equation by e², we get e = 12. So each edge is 12 inches or 1 foot long.

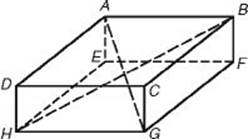
A diagonal of a rectangular solid is a line segment joining a vertex on one face of the box to the vertex on the opposite face that is furthest away. A rectangular solid has four diagonals, all the same length. In the following box, diagonals AG and BH are drawn in. The other two diagonals areCE and DF.

Key Fact K3

If the dimensions of a rectangular solid are , w, and h and if d is the length of a diagonal, then .

The formula given in KEY FACT K3 is obtained by using the Pythagorean theorem twice. In the figure below, is the diagonal of rectangular face BCDE. By BD the Pythagorean theorem, (BD)² = ² + w². Now ΔADB is a right triangle, and by the Pythagorean theorem:

TIP

The distance between any two points can always be calculated using the Pythagorean theorem.

EXAMPLE 2: To determine the length of a diagonal of a cube whose sides are e, use the formula from KEY FACT K3, noting that = w = h = e. Then, .