SAT SUBJECT TEST MATH LEVEL 1

SOLID AND COORDINATE GEOMETRY

CHAPTER 13
Coordinate Geometry

Exercises

1. What is the equation of the line that passes through (3, –3) and (3, 3)?

(A) x = 3

(B) y = 3

(C) y = 3x

(D) y = 3x + 3

(E) y = 3x – 3

2. What is the equation of the line whose x- and y-intercepts are each 3?

(A) x = 3

(B) y = 3

(C) y = x + 3

(D) y = x – 3

(E) y = –x + 3

3. What is the slope of the line that passes through (4, 3) and is parallel to the line that passes through (–3, 4) and (3, –4)?

(A)

(B)

(C)

(D) 1

(E)

4. What is the slope of the line that passes through (4, 3) and is perpendicular to the line that passes through (–3, 4) and (3, –4)?

(A)

(B)

(C)

(D) 1

(E)

5. If A (–1, 0) and B (3, –2) are two adjacent vertices of square ABCD, what is the area of the square?

(A) 12

(B) 16

(C) 20

(D) 25

(E) 36

Questions 6 and 7 refer to circle O, in which A (–1, 0) and B (3, –2) are the endpoints of a diameter.

6. What is the area of circle O?

(A) 2.5π

(B) 5π

(C) 6.25π

(D) 10π

(E) 20π

7. Which of the following is the equation of circle O?

(A) (x + 1)² + (y – 1)² =

(B) (x – 1)² + (y + 1)² =

(C) (x + 1)² + (y – 1)² = 5

(D) (x – 1)² + (y + 1)² = 5

(E) (x – 1)² + (y + 1)² = 25

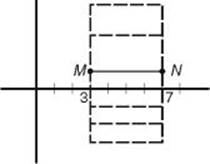
8. If M (3, 1) and N (7, 1) are two adjacent vertices of a rectangle, which of the following could not be one of the rectangle’s other vertices?

(A) (3, 7)

(B) (7, 3)

(C) (3, –7)

(D) (–3, 7)

(E) (7, 7)

9. Which of the following is the equation of a parabola that does NOT intersect the x-axis?

(A) y = x⁴ + 1

(B) y = x ² + 2x – 3

(C) y = (x – 1)²

(D) y = x ² – 1

(E) y = x ² + 1

10. What is the slope of the line that passes through (a, b) and ?

(A) 0

(B)

(C)

(D)

(E) The slope is undefined.

11. Line is tangent to the circle whose center is at (3, 2). If the point of tangency is (6, 6), what is the slope of line ?

(A)

(B)

(C) 0

(D)

(E)

Questions 12–14 concern the parabola whose equation is y = x ² – 20x – 69.

12. Where does the graph of the parabola cross the y-axis?

(A) –69

(B) –3

(C) 23

(D) 69

(E) The graph does not cross the y-axis.

13. What is the sum of the x=coordinates of the points where the graph of the parabola crosses the x-axis?

(A) –69

(B) 0

(C) 20

(D) 69

(E) The graph does not cross the x-axis.

14. Which of the following is the parabola’s turning point?

(A) (–10, 231)

(B) (0, –69)

(C) (10, –169)

(D) (-3, 0)

(E) (23, 0)

15. What is the equation of the circle whose center is at the origin and that passes through the point (8, 15)?

(A) x ² + y ² = 15

(B) x ² + y ² = 17

(C) x ² + y ² = 289

(D) (x – 8)² + (y – 15)² = 17

(E) (x – 8)² + (y – 15)² = 289

ANSWERS EXPLAINED

Answer Key

Solutions

Each of the problems in this set of exercises is typical of a question you could see on a Math 1 test. When you take the model tests in this book and, in particular, when you take the actual Math 1 test, if you get stuck on questions such as these, you do not have to leave them out—you can almost always answer them by using one or more of the strategies discussed in the “Tactics” chapter. The solutions given here do not depend on those strategies; they are the correct mathematical ones.

See Important Tactics for an explanation of the symbol ⇒, which is used in several answer explanations.

1. (A) A quick sketch shows that the line that passes through (3, –3) and (3, 3) is vertical. By KEY FACT L8, its equation is x = 3.

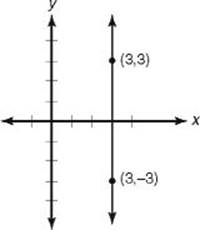
2. (E) Quickly sketch the line.

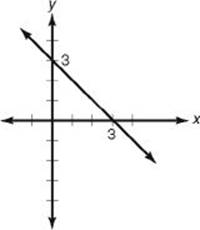
Since the line is neither horizontal nor vertical, its equation has the form y = mx + b. Since it crosses the y-axis at (0, 3), b = 3.

Since it passes through (0, 3) and (3, 0), its slope is , and so y = –1x + 3 or y = –x + 3.

Solutions 3 and 4. Before answering either question, quickly sketch line that goes through (–3, 4) and (3, –4) and lines ₁ and ₂, that go through (4, 3) and are parallel to and perpendicular to , respectively.

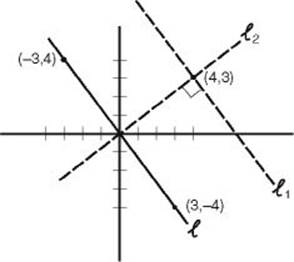
You should immediately see that the slope of ₁ is negative and the slope of ₂ is positive. So the answer to Question 3 must be A or B, and the answer to Question 4 must be C, D, or E.

3. (A) By KEY FACT L5, the slope of , the line through (–3, 4) and (3, –4) is

By KEY FACT L7, parallel lines have equal slopes, so the slope of ₁ is . Note that it is irrelevant that ₁ passes through (4, 3).

4. (C) From Solution 3, above, the slope of is . By KEY FACT L7, if two lines are perpendicular, the product of their slopes is –1. So if m is the slope of ₂, then:

As in Question 3, it is irrelevant that ₂ passes through (4, 3).

5. (C) From the distance formula (KEY FACT L3):

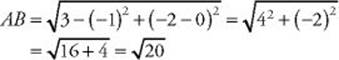
The area of square

6. (B) By the distance formula (KEY FACT L3):

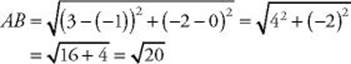
Since the diameter is , the radius is . Now use the area formula:

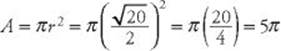
**Alternatively, you could have used the midpoint formula (KEY FACT L4) to determine that the center O is at

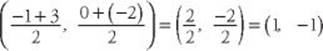
and then used the distance formula to find the length of radius .

7. (D) From the solution to Question 6, above, the radius of circle O is . From the alternative solution to Question 6, the center is at (1, –1). Finally, by KEY FACT J11, the equation of circle O is:

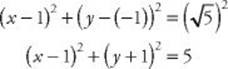
8. (D) Any point whose x-coordinate is 3 or 7 could be another vertex. Of the choices, only (–3, 7) could not be one of the vertices.

9. (E) A graph intersects the x-axis at points whose y-coordinates are 0. Choices B, C, and D all intersect the x-axis at (1, 0). Choices A and E do not intersect the x-axis, but Choice A is not the equation of a parabola.

10 (A) By KEY FACT L5, the formula for slope is . Before using it, though, look. Since the y-coordinates are equal, the numerator, and thus the fraction, equals 0.

11. (B) Draw a rough sketch

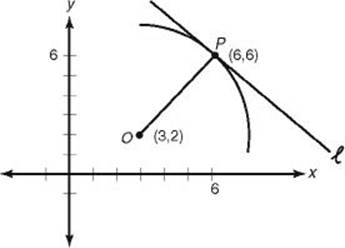
Line segment , joining (3, 2) and (6, 6) is a radius and so by KEY FACT L10 is perpendicular to line . The slope of is . Therefore, by -34 KEY FACT L7, the slope of is .

12. (A) Since the y-intercept of a graph is a point whose x-coordinate is 0, just evaluate the equation when x = 0:

y = 0² – 20(0) – 69 = –69

13. (C) The x-intercepts of the graph are the solutions of the equation x² – 20x – 69 = 0.

x² - 20x - 69 = 0 (x – 23)(x + 3) = 0
x = 23 or x = –3

The sum of the roots is 23 + (–3) = 20.

Since the question asks for the sum of the roots and not the individual roots, you can use KEY FACT E3—the formula for the sum of the roots:

14. (C) The turning point of the parabola is on the parabola’s axis of symmetry, whose equation is . So the x-coordinate of the turning point is 10; to get the y-coordinate, replace x by 10 in the equation of the parabola:

y = (10)² – 20(10) – 69 = 100 – 200 – 69 = –169.

The turning point is (10, –169).

15. (C) The equation of a circle whose center is at the origin is x ² + y ² = r² , where r is the radius. Since (8, 15) is on the circle, r² = 8² + 15² = 64 + 225 = 289. So the equation of this circle is x ² + y ² = 289.