SAT SUBJECT TEST MATH LEVEL 1
TRIGONOMETRY
![]()
CHAPTER 14
Basic Trigonometry
![]()
• Sine, Cosine, and Tangent
• What You Don”t Need to Know
• Exercises
• Answers Explained
This chapter is very short, because it does not review all the trigonometry you learned in school. It reviews only the trigonometry you need for the Math 1 test—which is not very much. The ONLY trigonometry you need to know for the Math 1 test are the meanings of the trigonometric ratios—sine, cosine, and tangent— and one simple identity.
SINE, COSINE, AND TANGENT
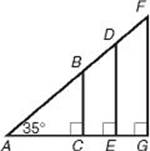
In the figure above, right triangles ABC, ADE, and AFG each have a 90° angle and a 35° angle, so they are all similar to one another. Therefore, their sides are in proportion:
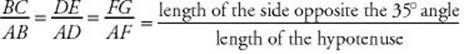
This ratio is called the sine of 35° and is written sin 35°. To evaluate sin 35°, you could very carefully measure the lengths of ![]() and
and ![]() and divide. In the given figure, FG
and divide. In the given figure, FG ![]() 1 inch, AF
1 inch, AF ![]() 1.75 inches, so
1.75 inches, so ![]() .
.
Fortunately, you do not have to do this. You can use your calculator. Depending on what calculator you use, you would either enter 35 and then press the ![]() button or press the
button or press the ![]() button and then enter 35. Regardless, in a fraction of a second, you will see the answer correct to several decimal places: sin 35° = 0.573576436, far greater accuracy than you need for the Math 1 test.
button and then enter 35. Regardless, in a fraction of a second, you will see the answer correct to several decimal places: sin 35° = 0.573576436, far greater accuracy than you need for the Math 1 test.
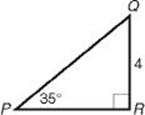
EXAMPLE 1: To find the length of hypotenuse ![]() in the triangle below, use the sine ratio (and your calculator):
in the triangle below, use the sine ratio (and your calculator):
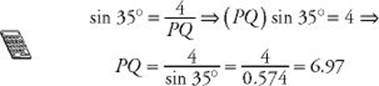
The formal definitions of the three trigonometric ratios you need are given in KEY FACT M1.
Key Fact M1
Let ![]() be one of the acute angles in a right triangle.
be one of the acute angles in a right triangle.
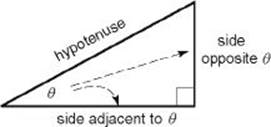
• The formula for the sine of ![]() , denoted sin
, denoted sin![]() , is:
, is:

• The formula for the cosine of ![]() , denoted cos
, denoted cos![]() , is:
, is:

• The formula for the tangent of ![]() , denoted tan
, denoted tan![]() , is:
, is:

• From the definitions of the three trigonometry ratios, it follows immediately that for any acute angle ![]() ,
, ![]()
For decades, students have remembered these definitions by memorizing the “word” SOHCAHTOA. For example, the “S” in “Soh” stands for “sine” and the “OH” reminds you that sine is Opposite over Hypotenuse.
The only trigonometric equation or identity you need to know other than those in KEY FACT M1, for the Math 1 test, is given in KEY FACT M2.
Key Fact M2
For any angle ![]() , sin2
, sin2![]() + cos2
+ cos2![]() = 1.
= 1.
Note that sin2![]() is an abbreviation for (sin
is an abbreviation for (sin![]() )2. So the identity sin2
)2. So the identity sin2![]() + cos2
+ cos2![]() = 1 means that if you take the sine of any angle and square it and then take the cosine of that same angle and square it, the sum of those two squares is 1.
= 1 means that if you take the sine of any angle and square it and then take the cosine of that same angle and square it, the sum of those two squares is 1.
For example, you can use your calculator to verify that (sin 37°)2+ (cos 37°)2 = 1. Note that in this identity, ![]() can be replaced by any expression at all. So sin2(4x + 1) + cos2(4x + 1) = 1.
can be replaced by any expression at all. So sin2(4x + 1) + cos2(4x + 1) = 1.
EXAMPLE 2: (3sin23![]() + 3cos23
+ 3cos23![]() – 1)2 = (3(sin23
– 1)2 = (3(sin23![]() + cos23
+ cos23![]() ) – 1)2 = (3(1) – 1)2 = (3 – 1)2 = 22 = 4.
) – 1)2 = (3(1) – 1)2 = (3 – 1)2 = 22 = 4.
If you know the value of any one of sin![]() , cos
, cos![]() , or tan
, or tan![]() , you can always find the values of the other two.
, you can always find the values of the other two.
EXAMPLE 3: If you are given that sin![]() =
= ![]() and want to know the 17 value of cos
and want to know the 17 value of cos![]() or tan
or tan![]() , draw right triangle ABC and label BC, the side opposite
, draw right triangle ABC and label BC, the side opposite ![]() , as 15 and the hypotenuse as 17.
, as 15 and the hypotenuse as 17.
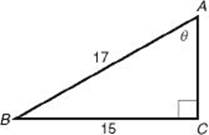
Now use the Pythagorean theorem to find AC:
(AC )2 + 152 = 172![]() AC2 + 225 = 289
AC2 + 225 = 289 ![]()
(AC )2 = 64 ![]() AC = 8.
AC = 8.
So ![]() and tan
and tan ![]()
If you were given that sin ![]() = 0.835, you would proceed exactly the same way. Draw a triangle and use the Pythagorean theorem to get
= 0.835, you would proceed exactly the same way. Draw a triangle and use the Pythagorean theorem to get
x 2 + (0.835)2 = 12![]() x 2 + 0.697 = 1
x 2 + 0.697 = 1 ![]() x 2 = 0.303
x 2 = 0.303 ![]() x = 0.55.
x = 0.55.
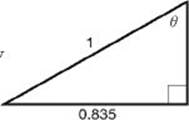
Now use SOHCAHTOA:
cos![]() =
= ![]() = 0.55= and tan
= 0.55= and tan![]() =
=![]() = 1.52
= 1.52
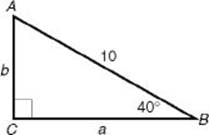
EXAMPLE 4: To find the values of a and b in the triangle below, use the trigonometric ratios.
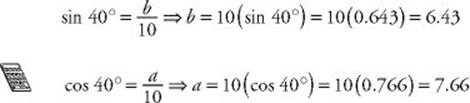
You could also be asked to find the measure of an angle ![]() if you are given the value of the sine, cosine, or tangent of that angle. For example, if you are given that sinq = 0.8, to find the value of
if you are given the value of the sine, cosine, or tangent of that angle. For example, if you are given that sinq = 0.8, to find the value of ![]() , you use your calculator to evaluate sin-1(0.8). On most calculators, SIN-1 is the second function button above the SIN button. So depending on your calculator, you would either press
, you use your calculator to evaluate sin-1(0.8). On most calculators, SIN-1 is the second function button above the SIN button. So depending on your calculator, you would either press ![]()
EXAMPLE 5: What is the measure of the smallest angle in a 3–4–5 triangle?
Draw and label the triangle, which you should immediately recognize as a right triangle.
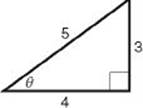
![]() By KEY FACT H3, the smallest angle is opposite the smallest side. So sin
By KEY FACT H3, the smallest angle is opposite the smallest side. So sin ![]() =
= ![]() and
and ![]() = sin–1
= sin–1![]() = 36.87°. Note that you can convert
= 36.87°. Note that you can convert ![]() to 0.6 and take sin–1(0.6), but that isn”t necessary.
to 0.6 and take sin–1(0.6), but that isn”t necessary.
EXAMPLE 6: A 20-foot ladder is leaning against a vertical wall. If the base of the ladder is 13 feet from the wall, what is the angle formed by the ladder and the ground?
Of course, you start by drawing a diagram.
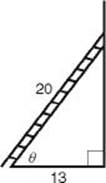
Then:
![]()