SAT SUBJECT TEST MATH LEVEL 1

FUNCTIONS

CHAPTER 15
Functions and Graphs

• Relations

• Functions

• Combining Functions

• Composition of Functions

• Inverse Functions

• Exercises

• Answers Explained

The concept of a function is one of the most fundamental notions in mathematics. In this chapter, you will see two equivalent definitions of function and then review the most important facts you need to know about functions for the Math 1 test.

RELATIONS

Since a function is a special type of relation, we will first review the definition of a relation. A relation is a set of ordered pairs. The first and second coordinates of the ordered pairs can be anything whatsoever, although on the Math 1 test they are almost always numbers. The number of ordered pairs in a relation can be finite or infinite. Each of the following sets is a relation:

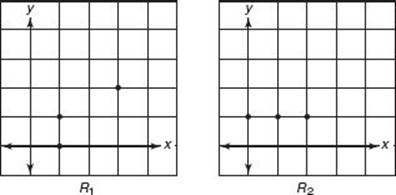
R₁ = {(1, 0), (1, 1), (3, 2)}

R₂ = {(0, 1), (1, 1), (2, 1)} = {(x, y)| x = 0, 1, or 2 and y = 1}

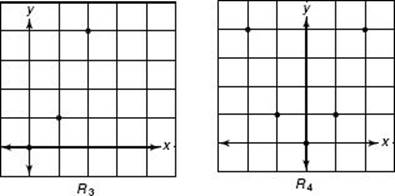
R₃ = {(0, 0), (1, 1), (2, 4)} = {(x, y)| y = x² and x = 0, 1, or 2}

R₄ = {(x, y)| y = x ² and x is an integer}

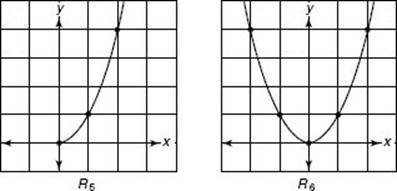
R₅ = {(x, y)| y = x² and x 0}

R₆ = {(x, y)| y = x ²}

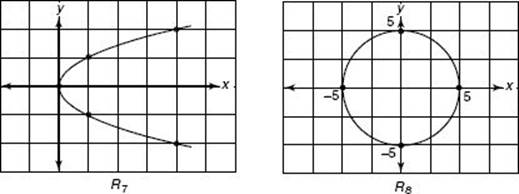
R₇ = {(x, y)| x = y ²}

R₈ = {(x, y)| x ² + y ² = 25}

R₉ = {(x, y)| x is a state in the United States and y is the capital of x}

R₁₀ = {(x, y)| x is a word in the English language and y is the number of letters in x}

R₁, R₂, R₃, R₉, and R₁₀ are finite sets with 3, 3, 3, 50, and approximately 400,000 elements, respectively. R₄, R₅, R₆, R₇, and R₈ are all infinite sets.

Note that (2, 4) is in R₃, R₄, R₅, and R₆; (–1, 1) is in R₄ and R₆; (, 2) is in R₅ and R₆; (4, 2) and (4, –2) are in R₇.

When the first and second coordinates of the ordered pairs are numbers, you can graph the pairs as explained in Chapter 13 on coordinate geometry. Here are the graphs of R₁, R₂, R₃, R₄, R₅, R₆, R₇, and R₈.