SAT SUBJECT TEST MATH LEVEL 1

FUNCTIONS

CHAPTER 15
Functions and Graphs

FUNCTIONS

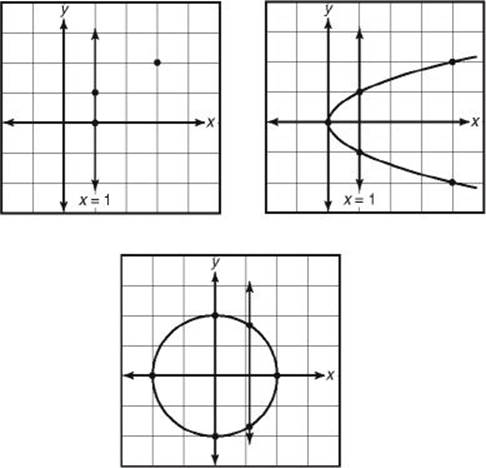
A relation is a function if no two of the ordered pairs in the relation have the same first coordinate and different second coordinates. Some, but not all, relations are functions. R₁ is not a function because two of its ordered pairs, (1, 1) and (1, 0), have the same first coordinates but different second coordinates. Similarly, R₇ and R₈ are not functions: (1, 1) and (1, –1) are both in R₇ and (3, 4) and (3, –4) are both in R₈. All of the other relations in the list above are functions.

EXAMPLE 1: If a and b are real numbers, and if

{(1, 2), (3, 4), (a, 6), (7, b)} is a function, what do we know about a and b?

Since a function cannot have two different ordered pairs with the same first coordinate, a cannot be 1 or 3 and a can be 7 only if b is 6. Other than that, there are no restrictions on a. If a is 7, b must be 6; if a is not 7, then b can be any number whatsoever.

If you look at the graphs of R₁, R₇, and R₈, the relations that are not functions, you can see that in each of them it is possible to draw at least one vertical line that intersects the graph in more than one point.

Key Fact N1

VERTICAL LINE TEST

A relation, R, is a function if and only if no vertical line can be drawn that intersects the graph of R more than once.

EXAMPLE 2: How many of the following graphs are graphs of functions?

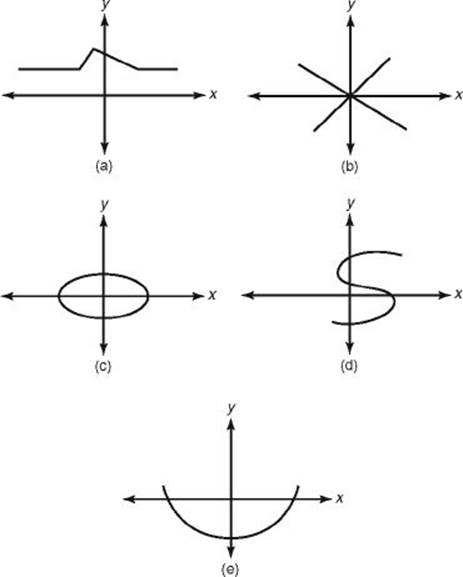
Graphs (a) and (e) satisfy the vertical line test. In contrast, in each of graphs (b), (c), and (d), the line x = 1 intersects the graph at least twice.

The domain of a function is the set of all the first components of the ordered pairs that make up the function. The range of a function is the set of all the second components of the ordered pairs that make up the function.

The following chart gives the domain and range of some of the functions in the list at the beginning of this section.

A function can also be defined as a rule that assigns to each element in one set an element in a second set.

For example, you can think of R₆ as the rule that assigns to each real number its square and R₉ as the rule that assigns to each state its capital. When we think of a function as a rule rather than as a set of ordered pairs, we often represent it by the letter f, although any letter could be used. In discussing three functions, we would use f, g, and h rather than f₁, f₂, and f₃.

When we treat a function as a rule, the domain is the set of all numbers to which the function assigns a second number, and the range is the set of those second numbers. For example, if f is the squaring function, since f assigns 25 to –5, –5 is in the domain of f and 25 is in the range of f.

As you have just seen, there is a function that takes any real number and squares it. In fact, your calculator has a button that performs that function. If you enter 123 on your calculator and then press the button, your calculator instantly assigns to 123 its square, 15,129, and displays it. Again, you can think of the squaring function as the set of ordered pairs R₆ = {(x, y)| y = x²} or as the rule, f, that assigns to each real number x its square, x², in which case you write f (x) = x². Note that

• f (2) = 2² = 4

• (2, 4) is in R₆

• (2, 4) a point on the graph of y = f (x) = x²

It is critically important that you understand function notation. When we write f (x) = x² + 3, we mean that f takes anything and assigns to it the square of that thing plus 3:

• f (anything) = (that thing)² + 3

• f (10) = 10² + 3 = 103

• f (0) = 0² + 3 = 3

• f (a) = a² + 3

• f (x + 1) = (x + 1)² + 3 = x² + 2x + 4

• f (x²) = (x²)² + 3 = x⁴ + 3

• f (2^x) = (2^x)² + 3 = 2^2x+ 3

• f (f (x)) = (f (x))² + 3 = (x² + 3)² + 3 = (x⁴ + 6x² + 9) + 3 = x⁴ + 6x² + 12

Typically, there are about six questions on functions on the Math 1 test. Two of them occur among the first 25 questions and are relatively easy. The first, and easiest, will probably ask you to evaluate a function for one particular value of x, as in Example 3. A slightly more difficult question might involve algebra, as in Example 4. The four other questions on functions will deal with more advanced topics that will be discussed later in this chapter.

EXAMPLE 3: If f (x) = –2x² – 2x – 2, what is f (–3)?

EXAMPLE 4: If f (x) = x² + 3, what is f (a + b) – f (a – b)?

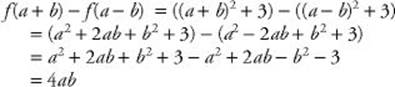
As you have already seen, since every real number can be squared, the domain of R₆, the squaring function, is the set of all real numbers. The domain of a function, however, can always be restricted by limiting the permissible x values. For example, the domain of R₃ = {(x, y)|y = x² and x = 0, 1, 2} is just the set {0, 1, 2}, and the domain of R₅ = {(x, y)|y = x² and x 0} is the set of non-negative numbers. Note that limiting the domain may or may not affect the range. The range of R₃ = {0, 1, 4}, but the range of R₅ is the same as the range of R₆: {y | y 0}. In the absence of any stated restriction, the domain of a function, y = f (x), described by a rule is the set of all real numbers except those for which f (x) is undefined. On the Math 1 test, there are only two ways for a function to be undefined for some number a: when trying to evaluate f (a) would involve (i) dividing by 0 or (ii) taking the square root, fourth root, or any even root of a negative number.

Key Fact N2

Unless specifically restricted, the domain of a function, y = f (x), consists of all real numbers x except those for which f (x) is undefined. A real number a is excluded from the domain of y = f (x) if evaluating f (a) would require

• Dividing by zero.

• Takng ia square root (or any even root) of a negative number.

EXAMPLE 5: The domain of consists of all real numbers except 2, which would cause the denominator to be 0, and numbers greater than 4, which would cause the expression under the square root sign to be negative.

The domain of f (x) is {x|x 4 and x 2}.

In general, determining the range of a function is much harder than determining the domain of the function. Fortunately, questions on the Math 1 test that deal with range are straightforward and present no serious problems.

If you think of a function as a machine, the domain consists of those numbers that the machine will accept as inputs (the x values). The range consists of those numbers that come out of the machine (the y values).

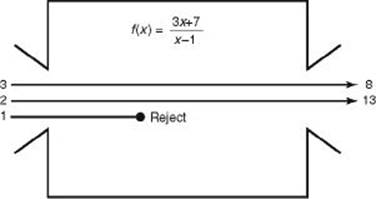
The machine above rejects 1 as an input since f (1) is undefined. No other number, however, causes a problem. The domain of f is the set of all real numbers not equal to 1. From the diagram you can see that since f (2) = 13 and f (3) = 8, 13 and 8 are both in the range. Obviously, lots of other numbers are too. Since 100, π, and –83 are all in the domain, when 100 and π and –83 go in, some numbers come out. However, does ever come out? How about , or 23? The answer is certainly not obvious.

In fact, all of those numbers are in the range. The only number that is not in the range is 3. To verify that 3 is not in the range, note that if 3 were in the range, there would be some number a such that f (a) = 3. However,

However, if 3a + 7 = 3a – 3, then, subtracting 3a from each side, we get that 7 = –3, which clearly is wrong!

If you graph , you will see that the graph does not cross the horizontal line y = 3.

Key Fact N3

For any real number b, b is in the range of f (x) if and only if the horizontal line y = b intersects the graph of y = f (x).

Graphing is actually a good way to determine the range, but on the Math 1 test, most range questions are easy enough to answer without graphing.

EXAMPLE 6: What is the range of f (x) = 3x + 5? The range of any linear function whose graph is not horizontal is the set of all real numbers. If b is any real number then

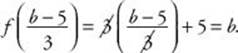
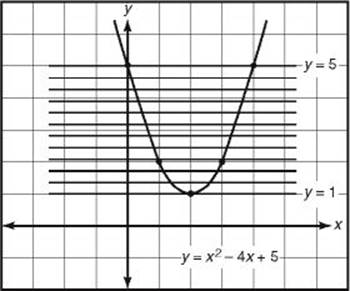
EXAMPLE 7: What is the range of f (x) = x² – 4x + 5? The graph of y = x² – 4x + 5 is a parabola that opens upward, whose axis of symmetry is , and whose turning point is (2,1). (See Chapter 13.) So the range is {y | y 1}. If you graph y = x² – 4x + 5 on your calculator, you can see that for each b 1, the line y = b would intersect the parabola.

As you have already seen, the graph of a function, f, is the set of all ordered pairs (x, y) such that y = f (x). On the Math 1 test, you won”t have to draw graphs, but you may have to recognize and work with them.

Sometimes you are given a graph and asked which of the five answer choices is the equation of that graph.

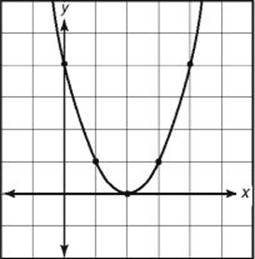
EXAMPLE 8: Which of the following could be the equation of the graph shown in the figure above?

(A) y = –2x + 4

(B) y = 2x + 4

(C) y = x²

(D) y = 2x² – 4

(E) y = x² – 4x + 4

Solution. Since the graph passes through (2, 0), x = 2 and y = 0 must satisfy the equation. Test each of the five choices.

So the answer is A or E. A, however, is the equation of a line, so the answer must be E. If you didn”t notice that, then to break the tie, you would just try another point on the graph, say (0, 4). Unfortunately, in both equations A and E, when x = 0, y = 4; so testing (0, 4) didn”t help. Try one more point: (1, 1). Now choice A does not work 1 –2(1) + 4, but choice E does work: 1 = 1² –4(1) + 4. The answer is E.

Another way the Math 1 test can test your understanding of the graphs of functions is to give you an equation and ask which of five graphs is the graph of the given equation.

EXAMPLE 9: Which of the following is the graph of y = |x² – 4x + 2|?

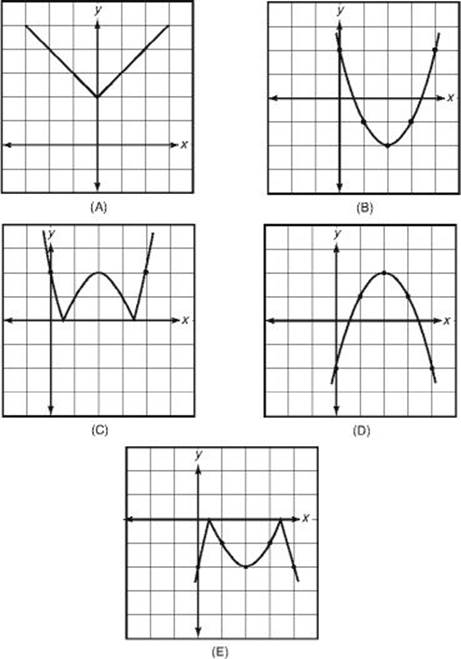
If you have a graphing calculator (and if you know how to enter absolute values), you can enter the equation and graph it. You should immediately be able to tell which of the answer choices is correct.

Finding the solution without using a calculator is just as easy. Since the absolute value of a number can never be negative, no point on the graph of y = |x² – 4x + 2| can be below the x-axis. Eliminate choices B, D, and E. Then just test any number. For example, if x = 1, then y = |1 – 4 + 2| = |–1| = 1, so (1, 1) must be on the graph. (1, 1) is on graph C but not on graph A.

On the Math 1 test, there may be one question that shows you a graph and asks you which of five other graphs is related to the original one in a certain way. To answer such a question, you can either test points or use the six facts listed in the following KEY FACT.

Key Fact N4

If f(x) is a function and r is a positive number:

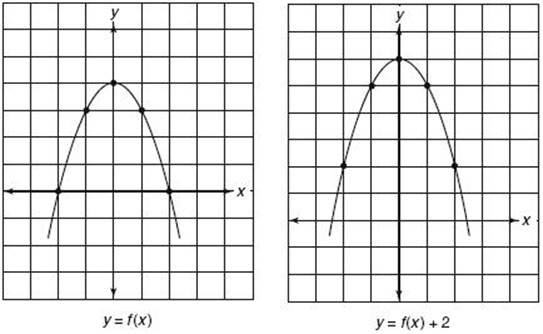
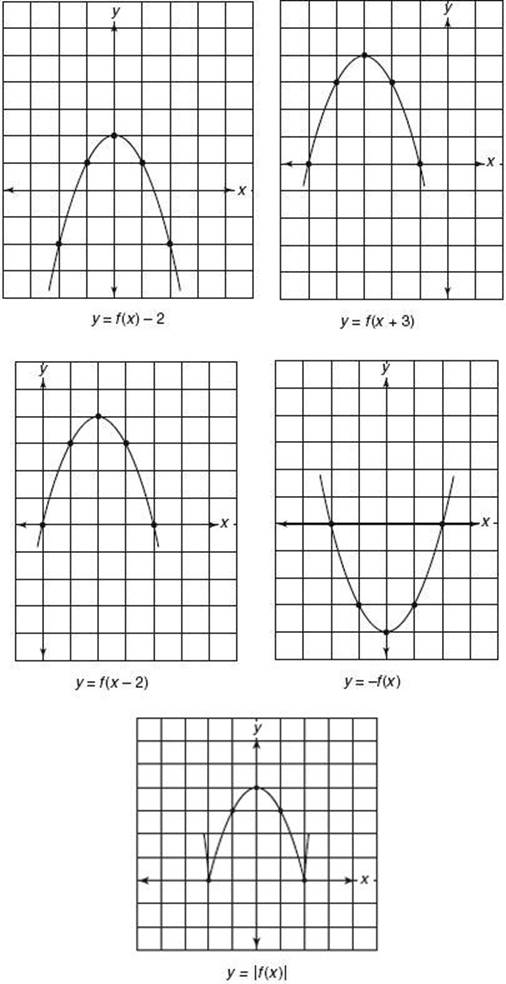
(1) The graph of y = f (x) + r is obtained by shifting the graph of y = f (x) UP r units.

(2) The graph of y = f (x) – r is obtained by shifting the graph of y = f (x) DOWN r units.

(3) The graph of y = f (x + r) is obtained by shifting the graph of y = f (x) r units to the LEFT.

(4) The graph of y = f (x – r) is obtained by shifting the graph of y = f (x) r units to the RIGHT.

(5) The graph of y = –f (x) is obtained by reflecting the graph of y = f (x) in the x-axis.

(6) The graph of y = | f (x)| consists of all the points on the graph of y = f (x) whenever f (x) 0 together with the reflection in the x-axis of those points on the graph of y = f (x) for which f (x) < 0.

Each part of KEY FACT N4 is illustrated in the following graphs.

The first graph is the graph of the function y = f (x) = 4 – x². The other six graphs are transformations of the original graph.