SAT SUBJECT TEST MATH LEVEL 1
FUNCTIONS
![]()
CHAPTER 15
Functions and Graphs
![]()
COMBINING FUNCTIONS
If f and g are two functions with overlapping—possibly equal—domains, then for all numbers x that are in both domains, it is possible to define the sum, difference, product, and quotient of f and g.
Key Fact N5
If x is in the domain of both f and g:
• (f + g)(x) = f (x) + g(x)
• (f – g)(x) = f (x) – g(x)
• (fg)(x) = f (x) • g(x)
• 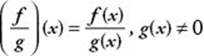
The only way KEY FACT N5 comes up on the Math 1 test is in evaluating the combination of two functions or in simplifying a quotient. If you need to evaluate the combination of functions, don”t actually combine them; use KEY FACT N5.
EXAMPLE 10: Let f (x) = 3x + 5 and g (x) = x2 + x – 5. To evaluate (fg)(2), you could first multiply f (x) • g (x):
f (x)g(x) = (3x + 5)(x2 + x – 5) = 3x 3 + 8x2 – 10x – 25
and then plug in x = 2:
3(23) + 8(22) – 10(2) – 25 = 24 + 32 – 20 – 25 = 11
but you shouldn”t. Instead you should evaluate first and then multiply:
(fg)(2) = f (2)g(2) = (3(2) + 5)(22 + 2 – 5) = (11)(1) = 11.
EXAMPLE 11: If f (x) = (x2 + x – 2), g (x) = (x2 – x – 2), h(x) = (x2 – 1), and x ![]() 1, –1, then:
1, –1, then: